Hi Shivkumar,

The text version of the answer
PQRS is a parallelogram in which A is the mid point of SR and B is a point on PR , such that BR = 1/4 PR if AB is produced it meets QR , at C prove that C is a mid point of QR
Given: PQRS is a parallelogram
A is mid-point of SR
and BR = 1/4 PR
To prove: C is mid-point of QR
Construction: Join SQ
Proof:
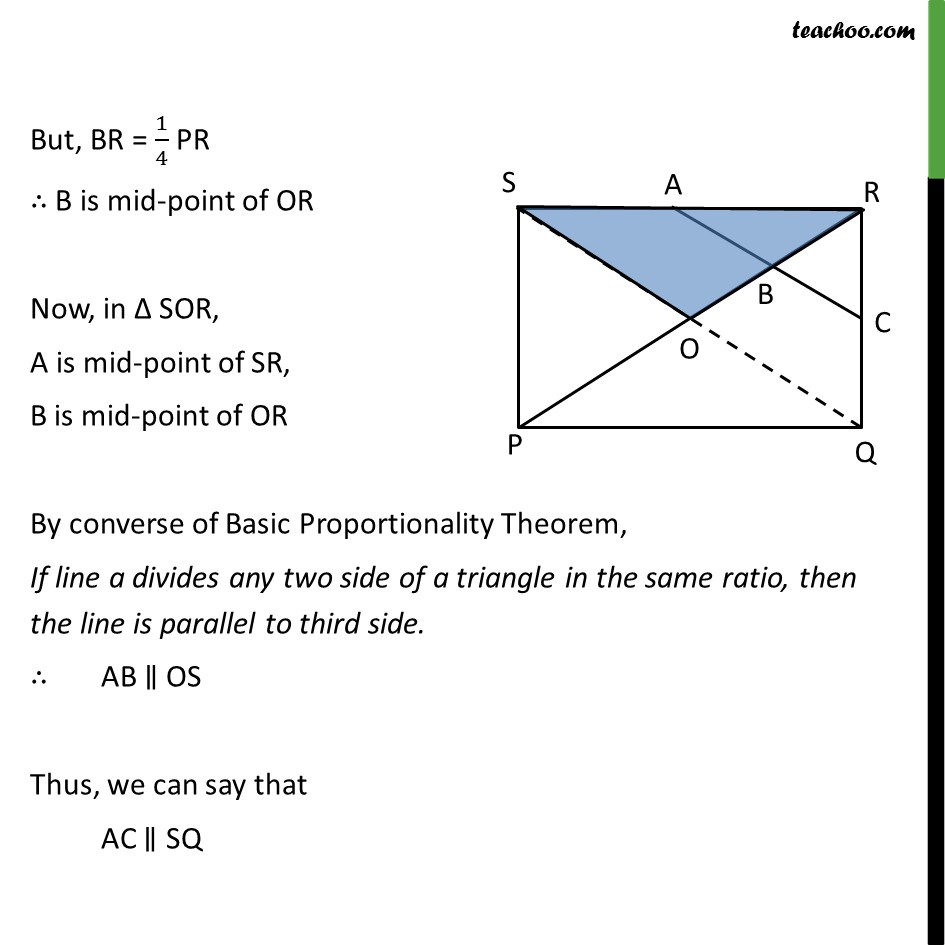
Since Diagonals of a parallelogram bisect each other,
OP = OR = 1/2 PR
But, BR = 1/4 PR
∴ B is mid-point of OR
Now, in Δ SOR,
A is mid-point of SR,
B is mid-point of OR
By converse of Basic Proportionality Theorem,
If line a divides any two side of a triangle in the same ratio, then the line is parallel to third side.
∴ AB ∥ OS
Thus, we can say that
AC ∥ SQ
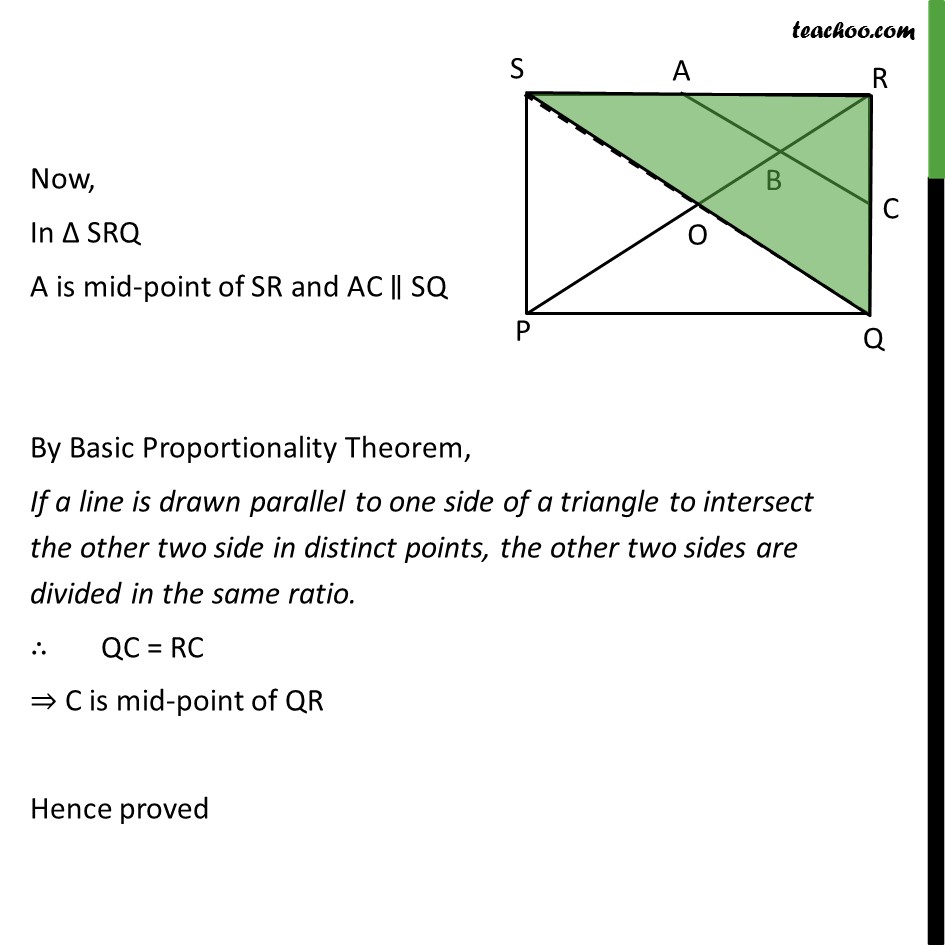
Now,
In Δ SRQ
A is mid-point of SR and AC ∥ SQ
By Basic Proportionality Theorem,
If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio.
∴ QC = RC
⇒ C is mid-point of QR
Hence proved
Written on Jan. 16, 2017, 9:08 p.m.