Introduction to Sets
Forget everything you know about numbers.
In fact, forget you even know what a number is.
This is where mathematics starts.
Instead of math with numbers, we will now think about math with "things".
Definition
What is a set? Well, simply put, it's a collection.
First we specify a common property among "things" (we define this word later) and then we gather up all the "things" that have this common property.
For example, the items you wear: hat, shirt, jacket, pants, and so on.
I'm sure you could come up with at least a hundred.
This is known as a set.
|
Or another example is types of fingers. This set includes index, middle, ring, and pinky. |
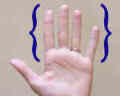 |
So it is just things grouped together with a certain property in common.
Notation
There is a fairly simple notation for sets. We simply list each element (or "member") separated by a comma, and then put some curly brackets around the whole thing:
The curly brackets { } are sometimes called "set brackets" or "braces".
This is the notation for the two previous examples:
{socks, shoes, watches, shirts, ...}
{index, middle, ring, pinky}
Notice how the first example has the "..." (three dots together).
The three dots ... are called an ellipsis, and mean "continue on".
So that means the first example continues on ... for infinity.
(OK, there isn't really an infinite amount of things you could wear, but I'm not entirely sure about that! After an hour of thinking of different things, I'm still not sure. So let's just say it is infinite for this example.)
So:
- The first set {socks, shoes, watches, shirts, ...} we call an infinite set,
- the second set {index, middle, ring, pinky} we call a finite set.
But sometimes the "..." can be used in the middle to save writing long lists:
Example: the set of letters:
{a, b, c, ..., x, y, z}
In this case it is a finite set (there are only 26 letters, right?)
Written on May 24, 2019, 2:08 a.m.

