Answer of this question

Hi Rishav,

Rhombus has all 4 sides equal,

So, Perimeter = 4 x Side of rhombus

146 = 4 x Side of Rhombus

146/4 = Side of Rhombus

36.5  = Side of Rhombus

Side of Rhombus = 36.5 cm

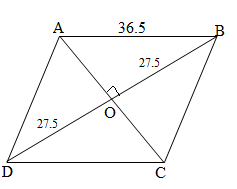
Thus, AB = BC = CD = AD = 27.5 cm

And given Diagonal BD = 55 cm

We need to find AC

Also, Diagonals of rhombus bisect each other at right angles,

Thus, angle AOB = 90

and OB = OD = BD/2 = 55/2 = 27.5

Now, AOB is a right angled triangle,

By Pythagoras Theorem

AB² = AO² + OB²

(36.5)2 = AO² + (27.5)²

(36.5)² - (27.5)² = AO²

AO² = (36.5)² - (27.5)²

AO² = (36.5 - 27.5) (36.5 + 27.5)

AO² = (9) (64)

AO = (3) (8)

AO = 24

Thus, AC = 2AO = 2(24) = 48 cm

Written on March 23, 2017, 12:06 p.m.