It is the length of the line segment which joins the point to the line and is perpendicular to the line.
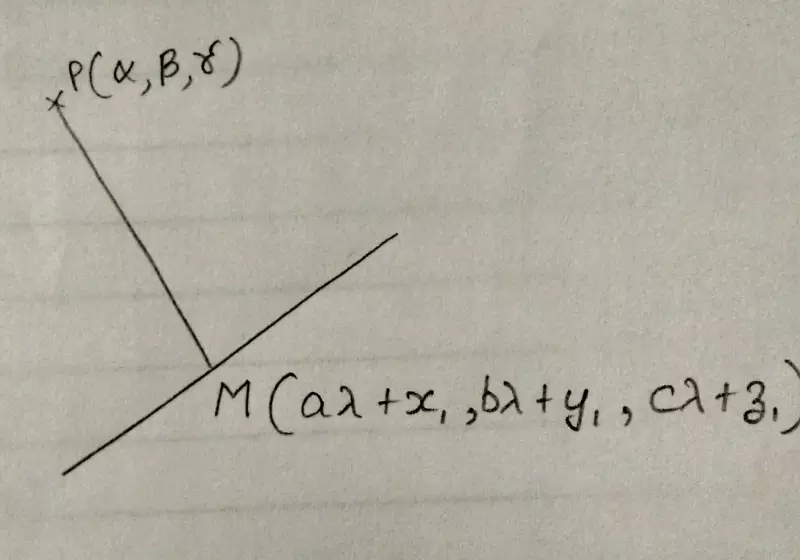
To find length of the perpendicular from the point, P(α,β,γ) on the line,
(x - x₁)/a=(y - y₁)/b=(z - z₁)/c
We can use the following method.
Any point on the given line,
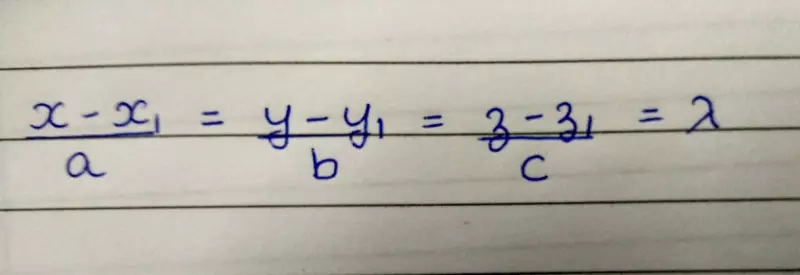
is given by, (aλ⁺x₁ , bλ⁺y₁ , cλ⁺z₁).
Thus the foot M of the perpendicular from P on the line will be of this form.
Let, M = (aλ⁺x₁ , bλ⁺y₁ , cλ⁺z₁)......①
Now the direction ratios of the perpendicular passing through two points P(α,β,γ) and M(aλ⁺x₁ , bλ⁺y₁ , cλ⁺z₁) are: (aλ⁺x₁- α) , (bλ⁺y₁- β) , (cλ⁺z₁- γ).
And direction ratios of the line are: a, b, c
Clearly PM is perpendicular to the line.
Therefore,
a(aλ⁺x₁- α) ⁺ b(bλ⁺y₁- β) ⁺ c(cλ⁺z₁- γ)=0
On solving this equation we get the value of λ and on substituting this value of λ in ①, we get the co-ordinates of M.
Now, length of the perpendicular PM from P on to the line can be obtained by applying distance formula.
The solution for one of your problem.

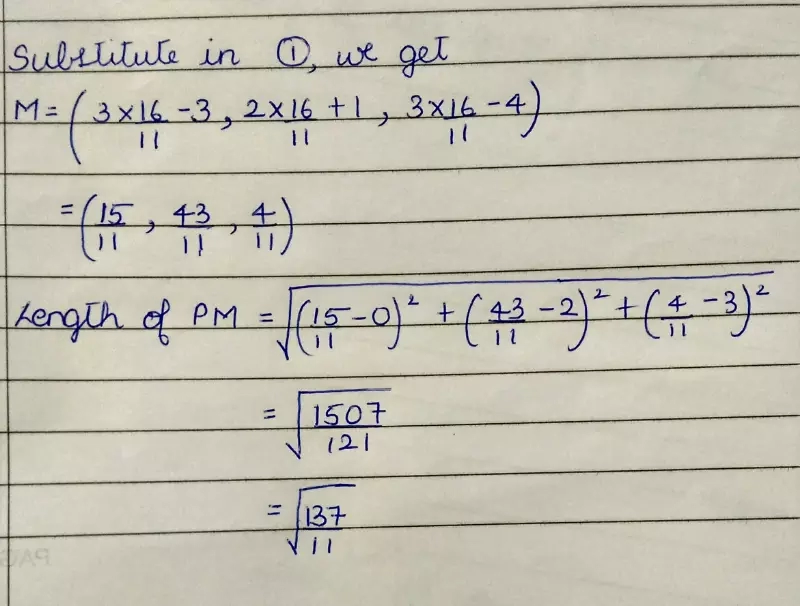
Written on March 13, 2017, 11:02 p.m.