Question 8 - Important questions on Parallelograms and Triangles - Areas of Parallelograms and Triangles

Transcript

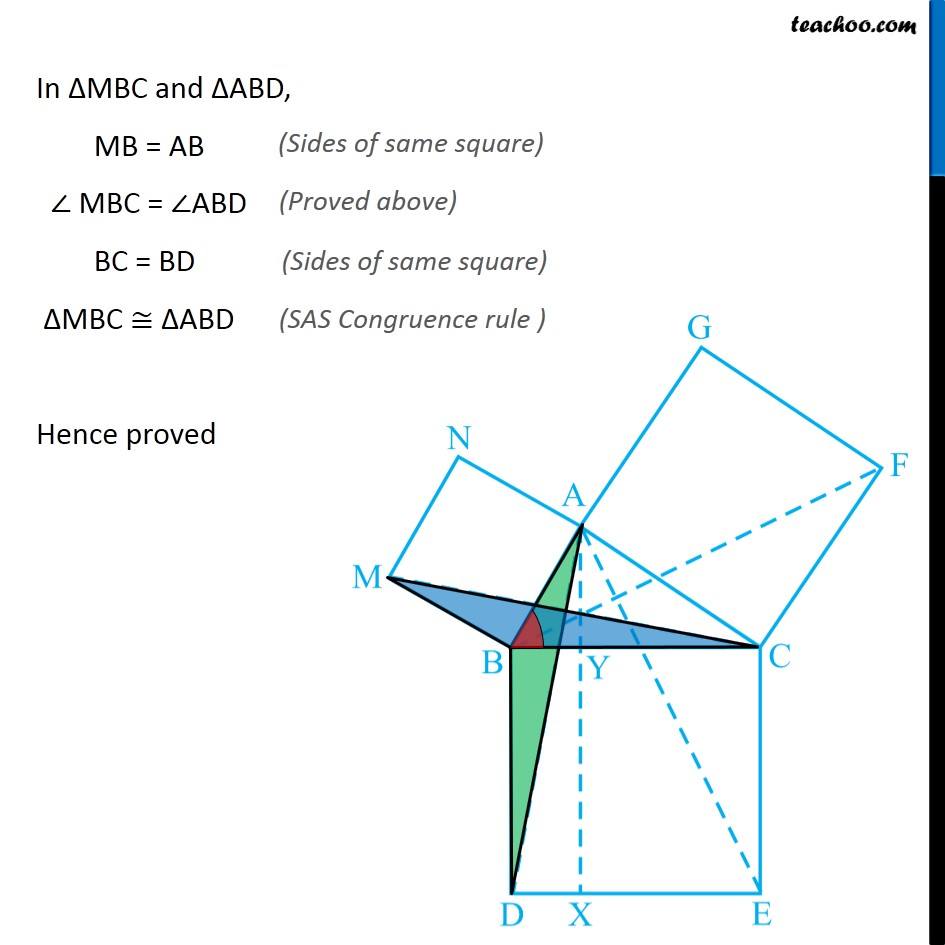
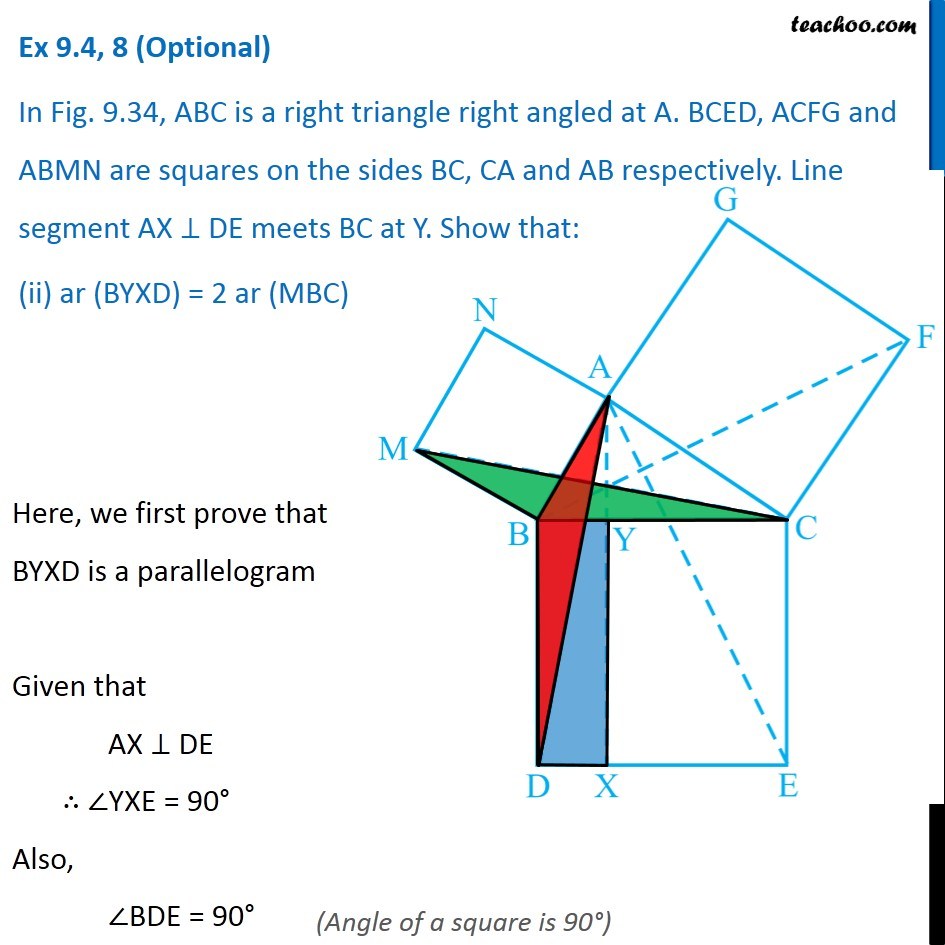
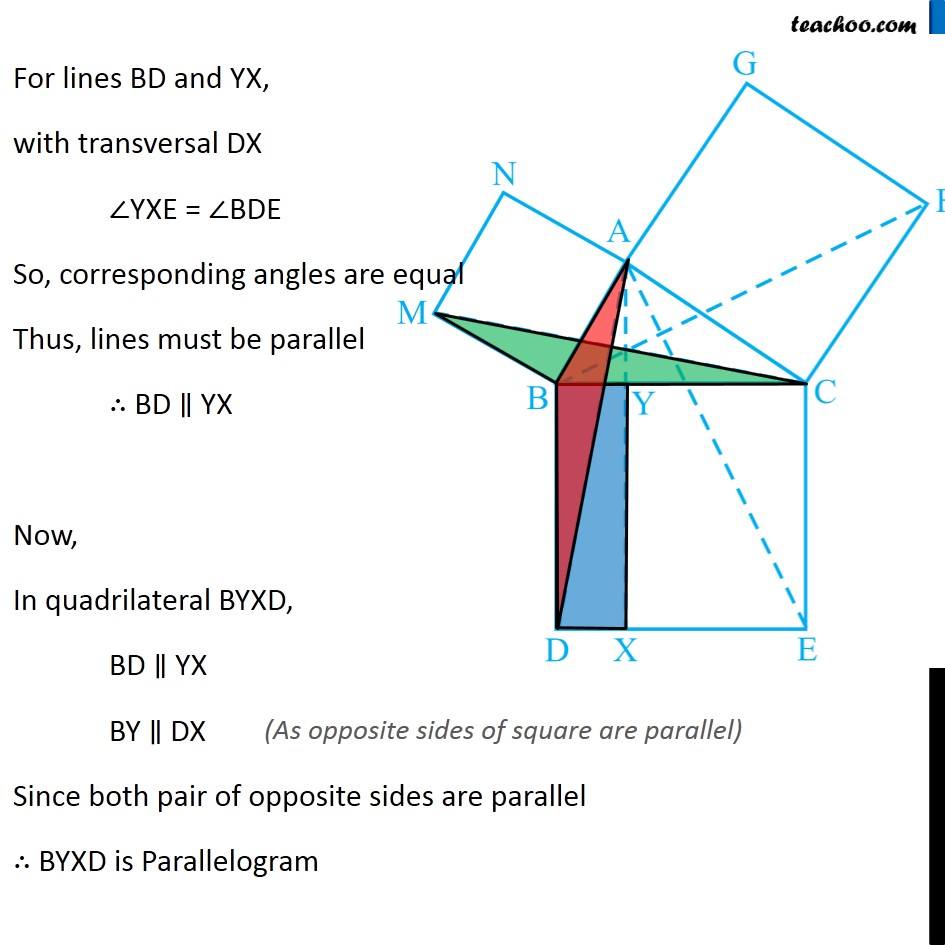
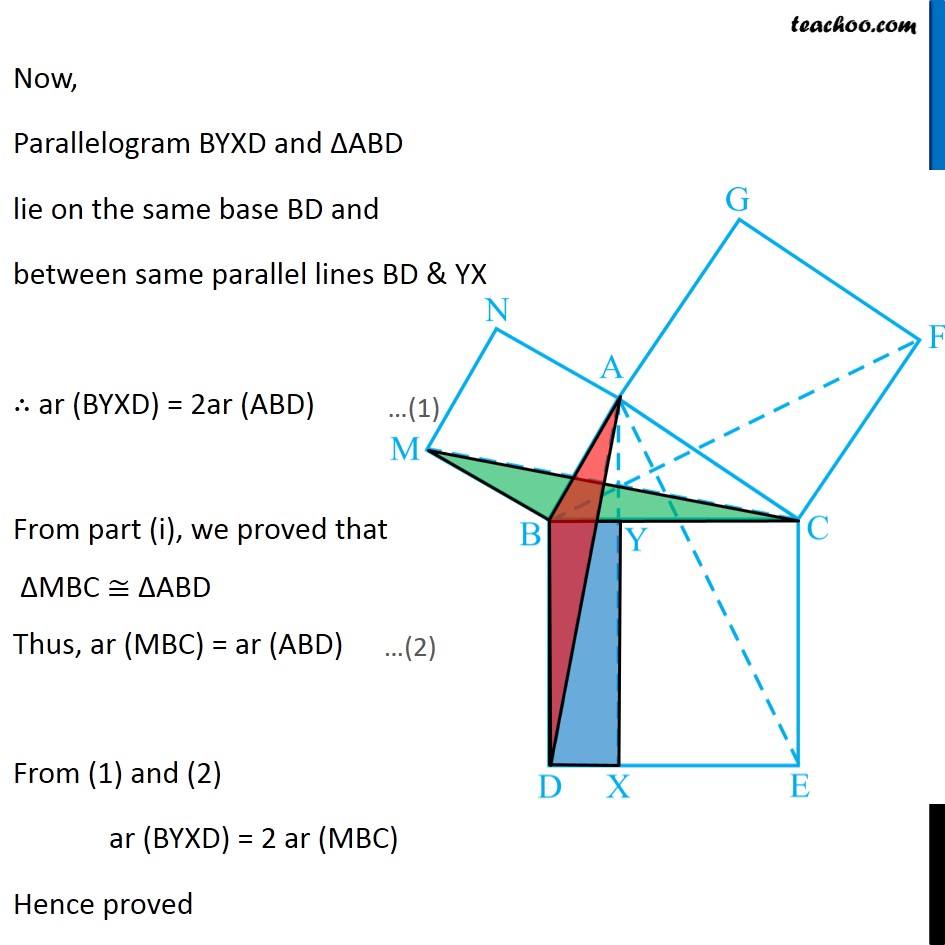
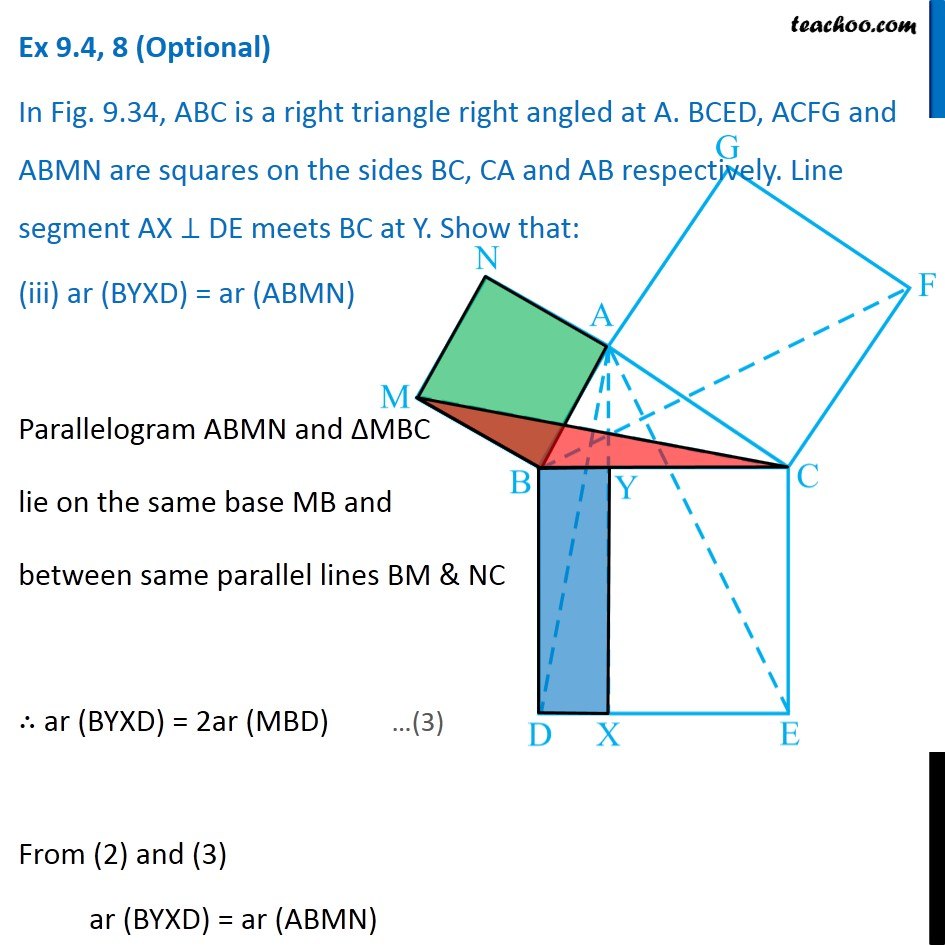
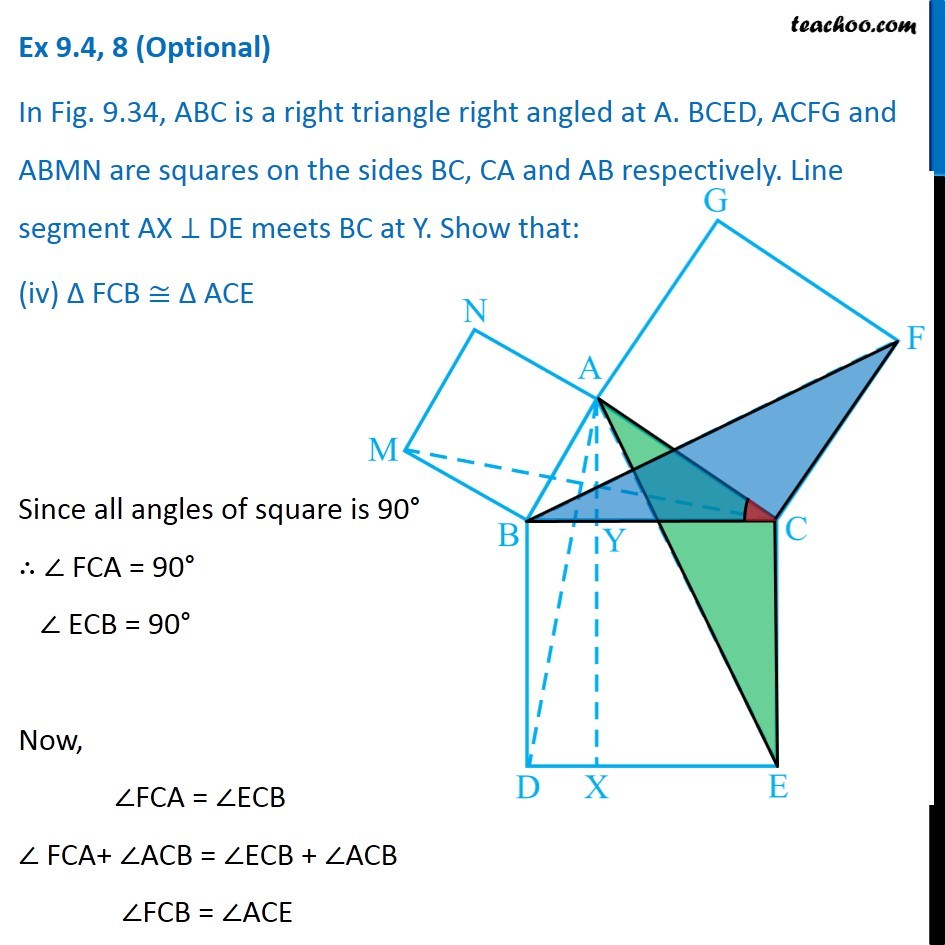
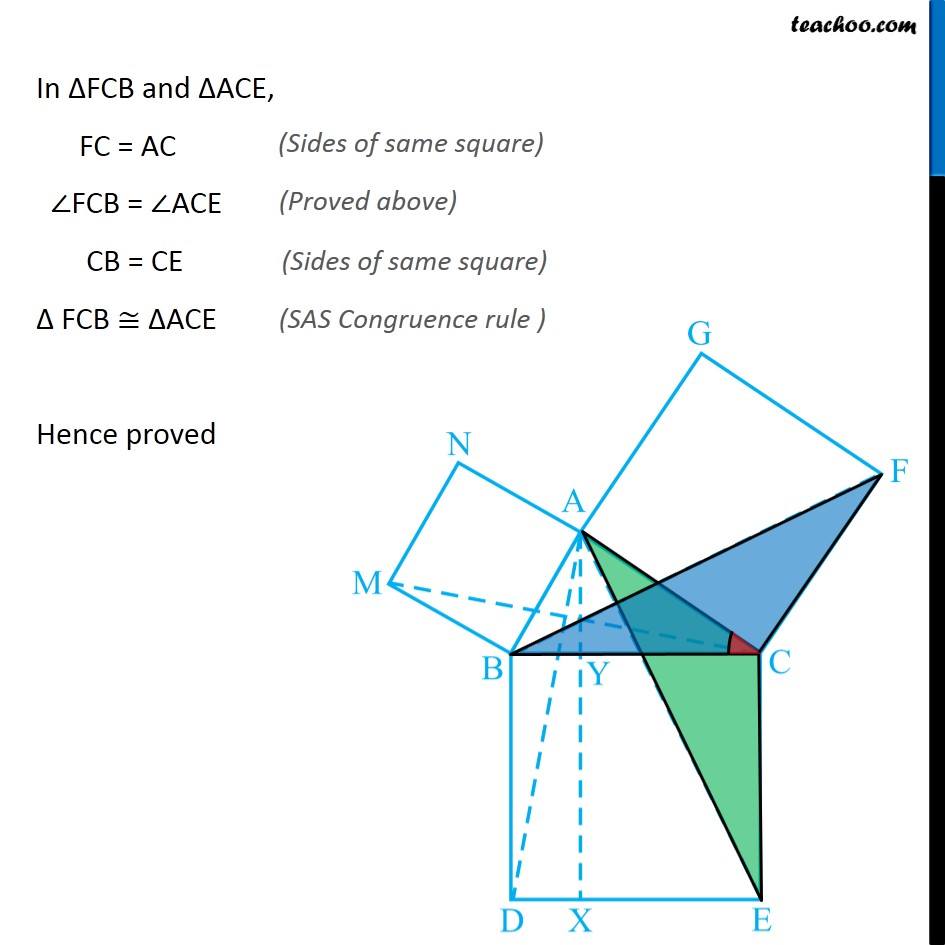
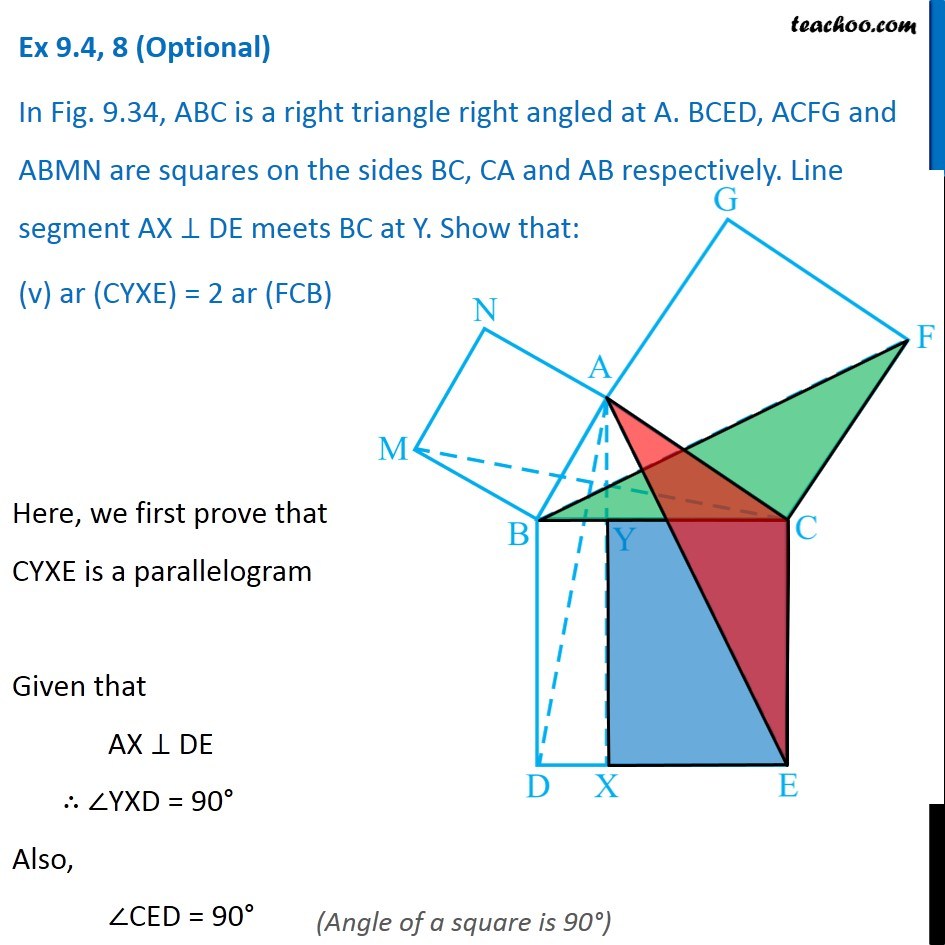
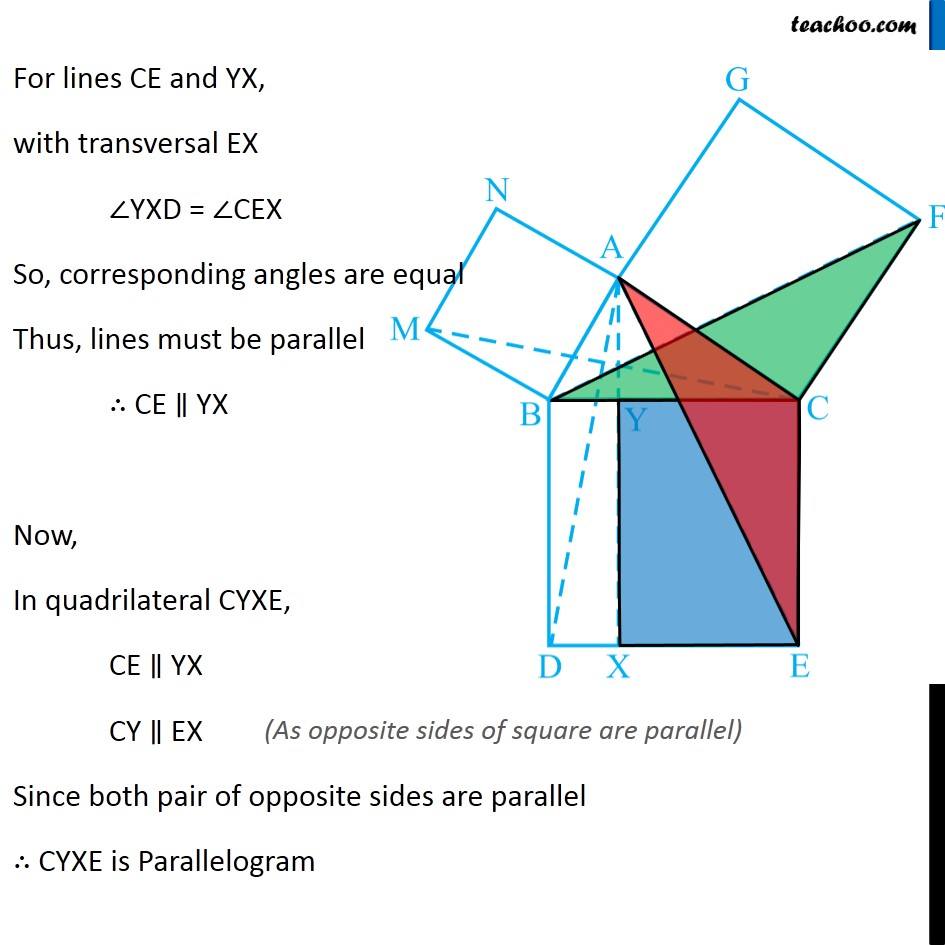
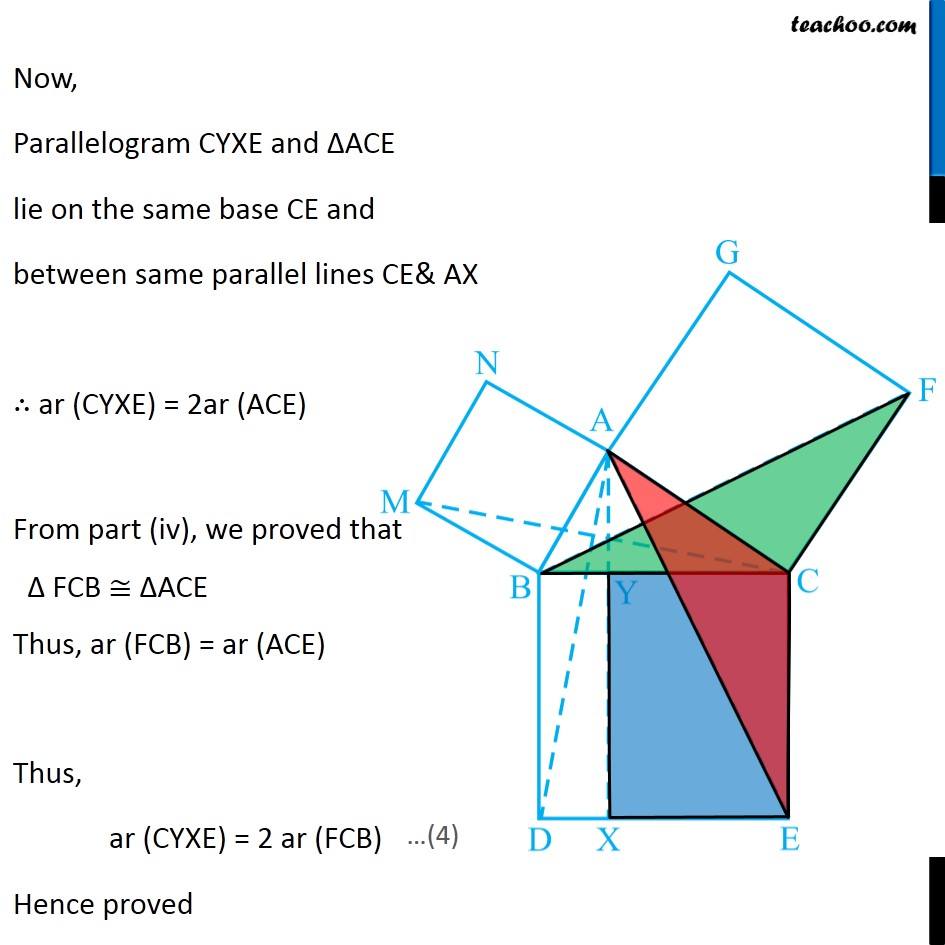
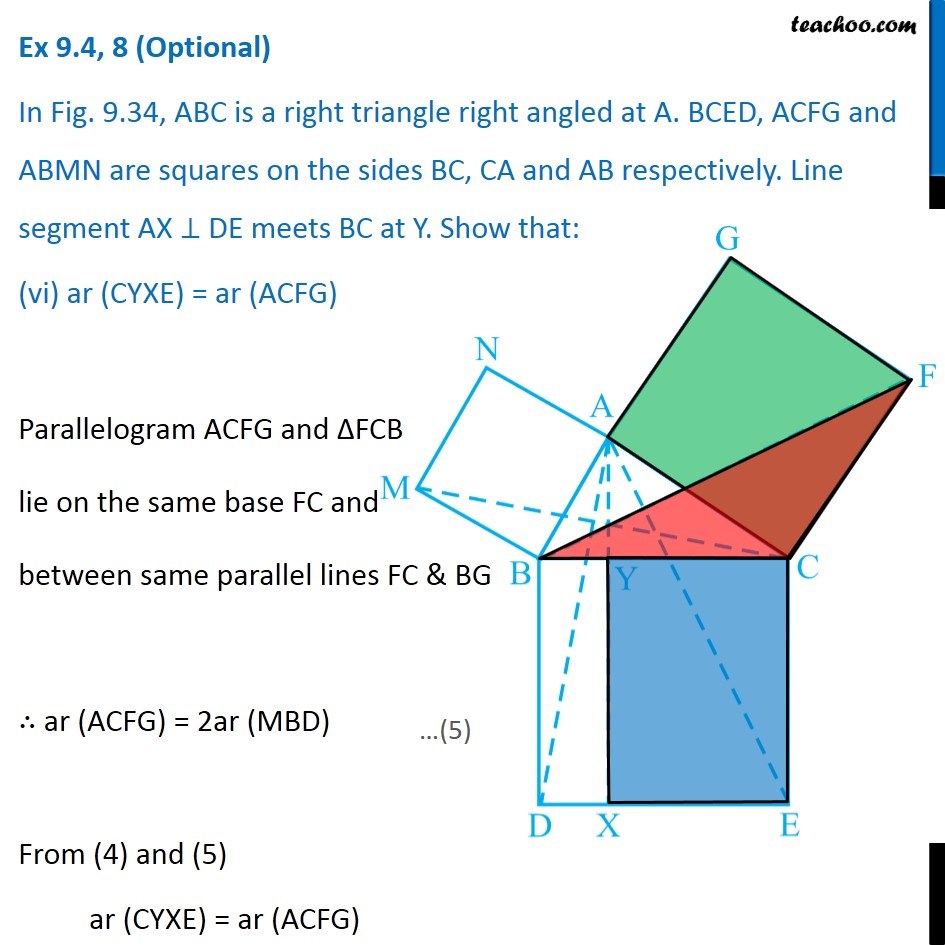
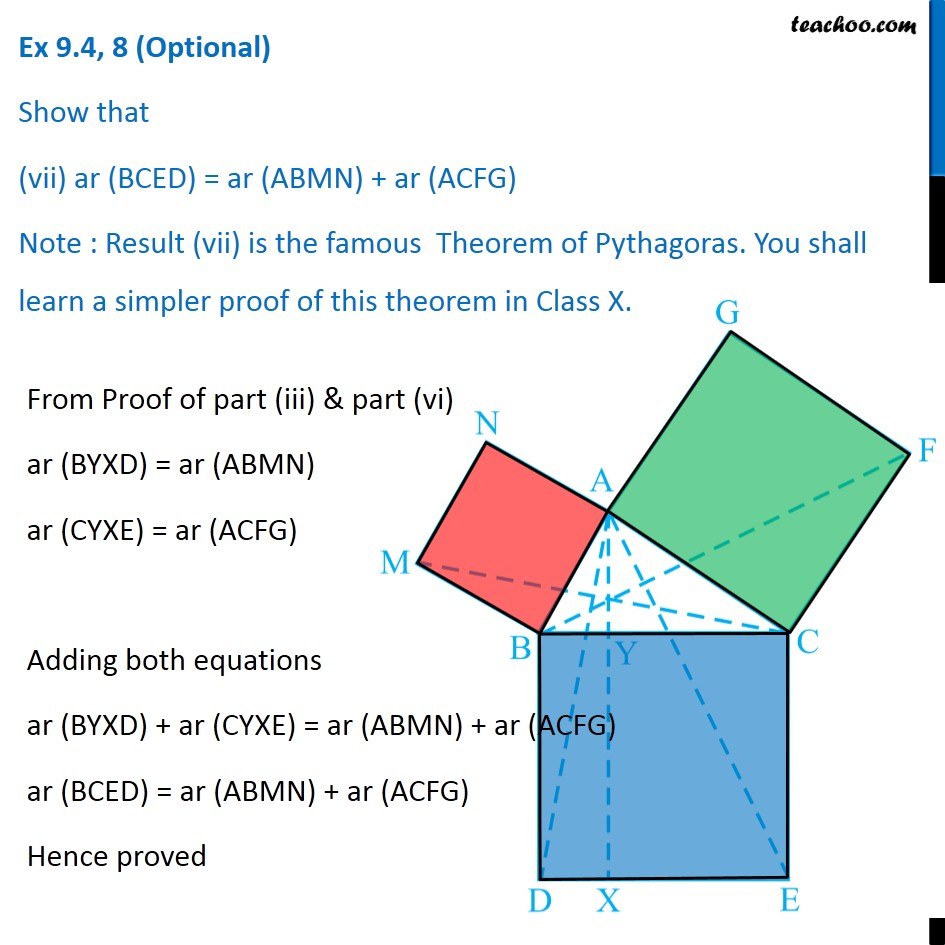
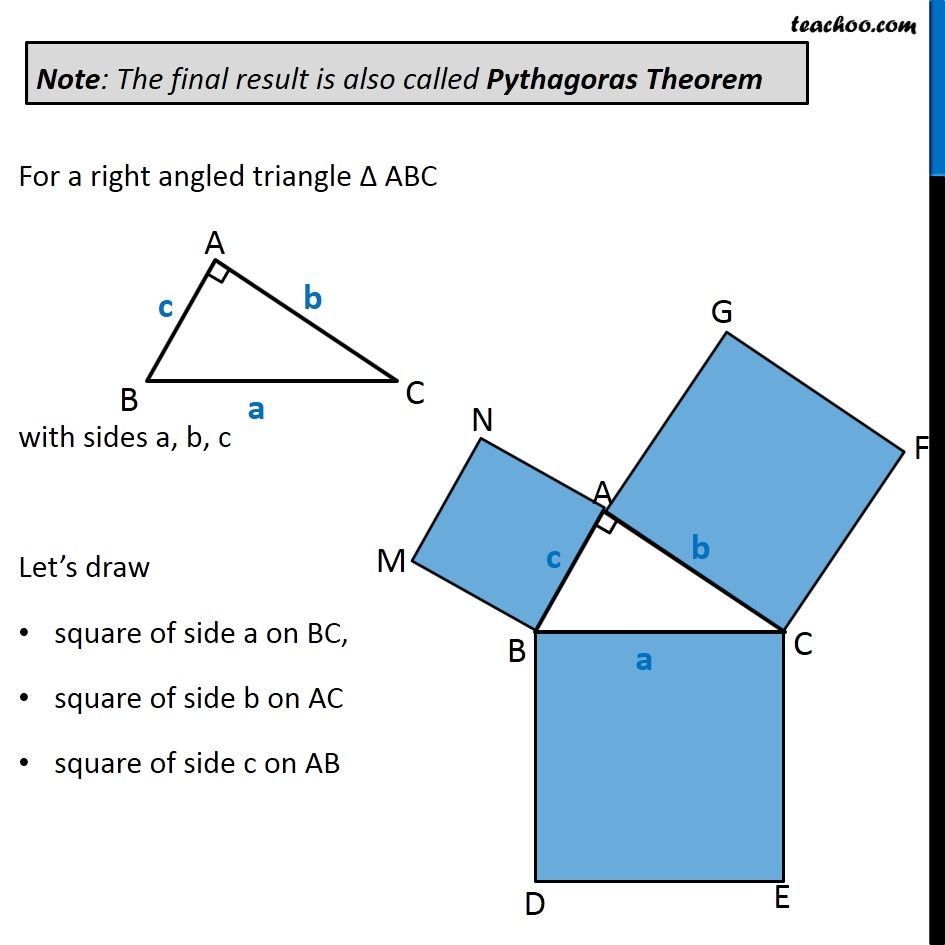
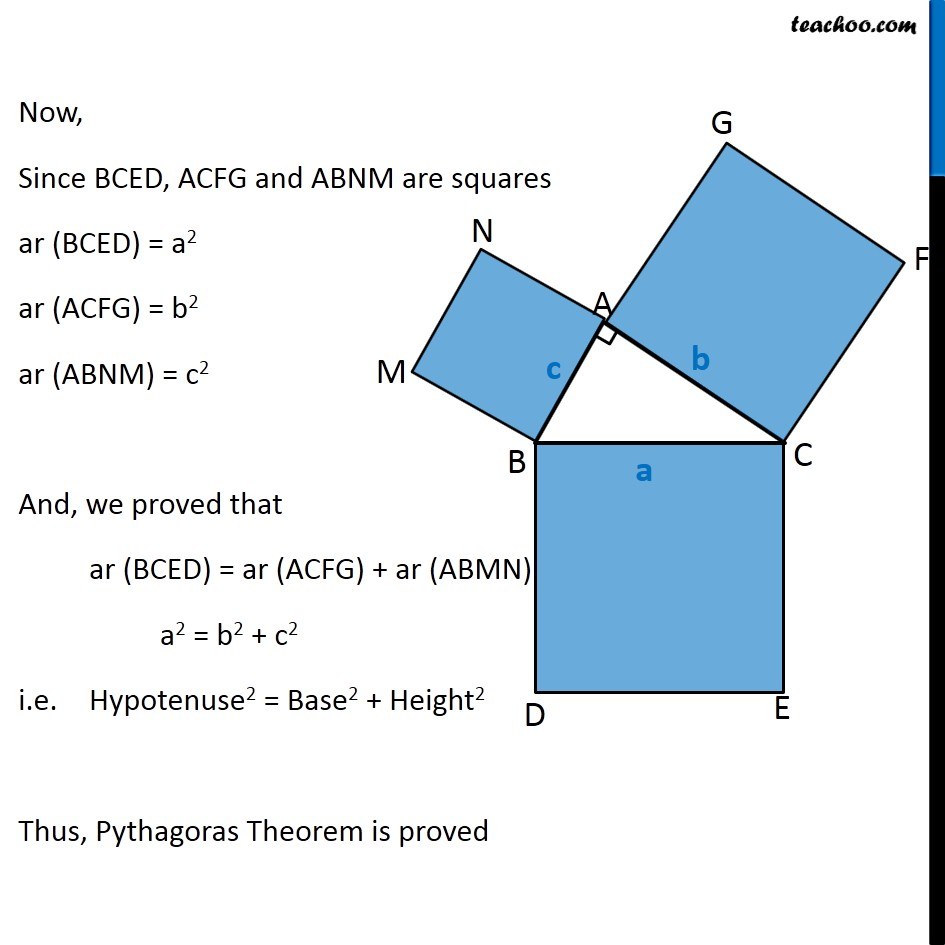
Question 8 In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that: ∆ MBC ≅ ∆ ABD Since all angles of square is 90° ∴ ∠ABM = 90° ∠DBC = 90° Now, ∠ABM = ∠DBC ∠ ABM + ∠ABC = ∠OBC + ∠ABC ∠MBC = ∠ABD In ∆MBC and ∆ABD, MB = AB ∠ MBC = ∠ABD BC = BD ∆MBC ≅ ∆ABD Hence proved (Sides of same square) (Proved above) (Sides of same square) (SAS Congruence rule ) Question 8 In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that: (ii) ar (BYXD) = 2 ar (MBC) Here, we first prove that BYXD is a parallelogram Given that AX ⊥ DE ∴ ∠YXE = 90° Also, ∠BDE = 90° (Angle of a square is 90°) For lines BD and YX, with transversal DX ∠YXE = ∠BDE So, corresponding angles are equal Thus, lines must be parallel ∴ BD ∥ YX Now, In quadrilateral BYXD, BD ∥ YX BY ∥ DX Since both pair of opposite sides are parallel ∴ BYXD is Parallelogram (As opposite sides of square are parallel) Now, Parallelogram BYXD and ∆ABD lie on the same base BD and between same parallel lines BD & YX ∴ ar (BYXD) = 2ar (ABD) From part (i), we proved that ∆MBC ≅ ∆ABD Thus, ar (MBC) = ar (ABD) From (1) and (2) ar (BYXD) = 2 ar (MBC) Hence proved Question 8 In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that: (iii) ar (BYXD) = ar (ABMN) Parallelogram ABMN and ∆MBC lie on the same base MB and between same parallel lines BM & NC ∴ ar (BYXD) = 2ar (MBD) From (2) and (3) ar (BYXD) = ar (ABMN) Question 8 In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that: (iv) ∆ FCB ≅ ∆ ACE Since all angles of square is 90° ∴ ∠ FCA = 90° ∠ ECB = 90° Now, ∠FCA = ∠ECB ∠ FCA+ ∠ACB = ∠ECB + ∠ACB ∠FCB = ∠ACE In ∆FCB and ∆ACE, FC = AC ∠FCB = ∠ACE CB = CE ∆ FCB ≅ ∆ACE Hence proved In ∆FCB and ∆ACE, FC = AC ∠FCB = ∠ACE CB = CE ∆ FCB ≅ ∆ACE Hence proved (Sides of same square) (Proved above) (Sides of same square) (SAS Congruence rule ) Question 8 In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that: (v) ar (CYXE) = 2 ar (FCB) Here, we first prove that CYXE is a parallelogram Given that AX ⊥ DE ∴ ∠YXD = 90° Also, ∠CED = 90° (Angle of a square is 90°) For lines CE and YX, with transversal EX ∠YXD = ∠CEX So, corresponding angles are equal Thus, lines must be parallel ∴ CE ∥ YX Now, In quadrilateral CYXE, CE ∥ YX CY ∥ EX Since both pair of opposite sides are parallel ∴ CYXE is Parallelogram Now, Parallelogram CYXE and ∆ACE lie on the same base CE and between same parallel lines CE& AX ∴ ar (CYXE) = 2ar (ACE) From part (iv), we proved that ∆ FCB ≅ ∆ACE Thus, ar (FCB) = ar (ACE) Thus, ar (CYXE) = 2 ar (FCB) Hence proved Question 8 In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that: (vi) ar (CYXE) = ar (ACFG) Parallelogram ACFG and ∆FCB lie on the same base FC and between same parallel lines FC & BG ∴ ar (ACFG) = 2ar (MBD) From (4) and (5) ar (CYXE) = ar (ACFG) Question 8 Show that (vii) ar (BCED) = ar (ABMN) + ar (ACFG) Note : Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X. From Proof of part (iii) & part (vi) ar (BYXD) = ar (ABMN) ar (CYXE) = ar (ACFG) Adding both equations ar (BYXD) + ar (CYXE) = ar (ABMN) + ar (ACFG) ar (BCED) = ar (ABMN) + ar (ACFG) Hence proved Note: The final result is also called Pythagoras Theorem For a right angled triangle Δ ABC with sides a, b, c Let’s draw square of side a on BC, square of side b on AC square of side c on AB Now, Since BCED, ACFG and ABNM are squares ar (BCED) = a2 ar (ACFG) = b2 ar (ABNM) = c2 And, we proved that ar (BCED) = ar (ACFG) + ar (ABMN) a2 = b2 + c2 i.e. Hypotenuse2 = Base2 + Height2 Thus, Pythagoras Theorem is proved