Question 4 - Important questions on Parallelograms and Triangles - Areas of Parallelograms and Triangles

Transcript

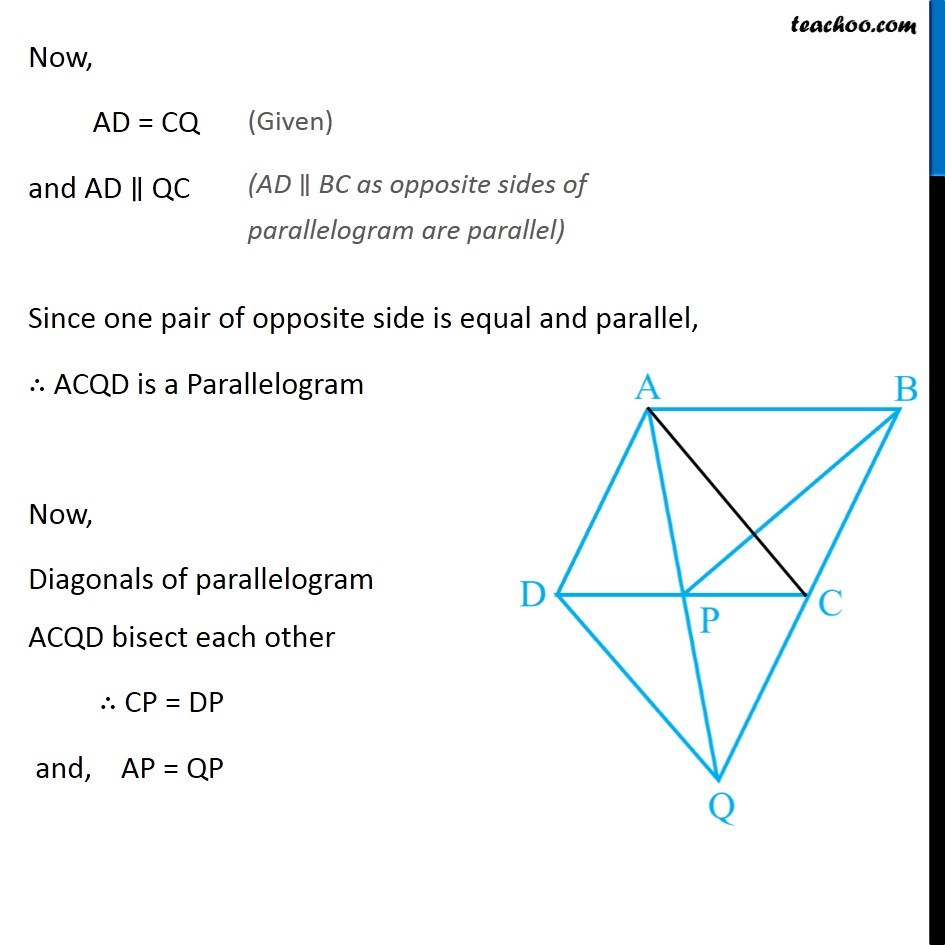
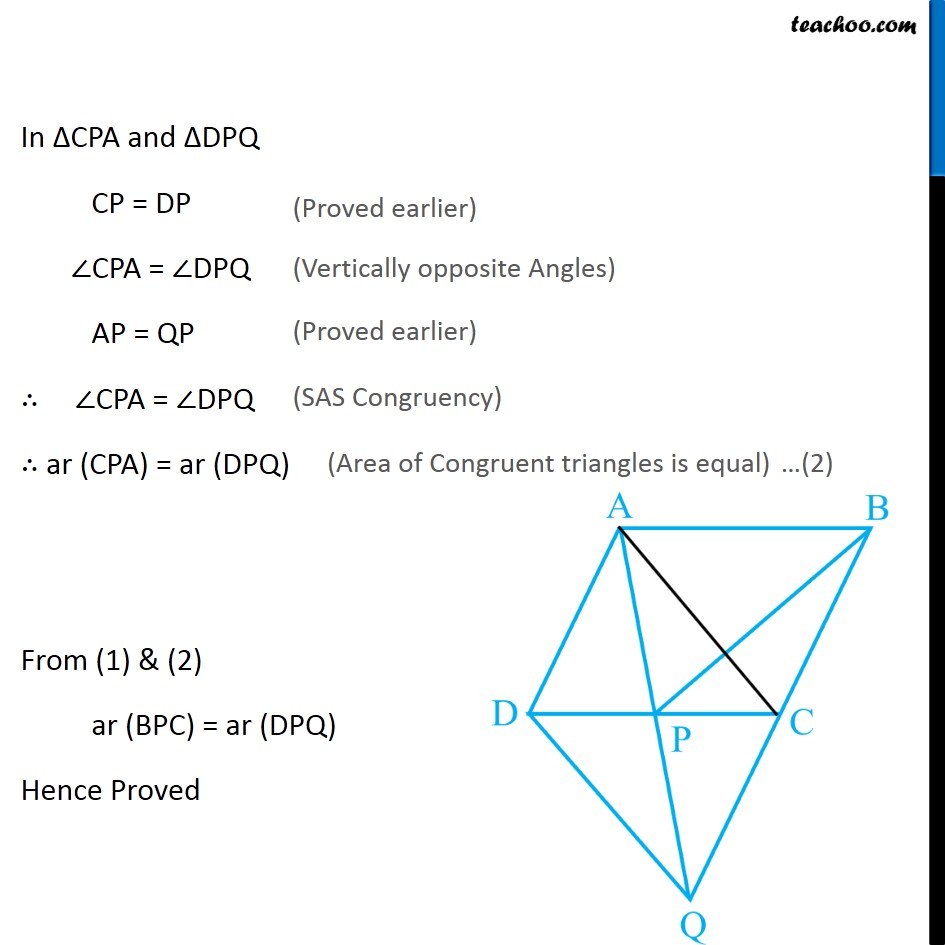
Question 4 In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ). [Hint : Join AC.] Given: ABCD is a parallelogram, AD = CQ To prove: ar (BPC) = ar (DPQ) Construction: Join AC. Proof: Here, ∆ ACP and ∆BPC are on the same base PC and between same parallels AB and CP. ∴ ar (ACP) = ar (BPC) (AB ∥ CD as opposite sides of parallelogram are parallel) Now, AD = CQ and AD ∥ QC Since one pair of opposite side is equal and parallel, ∴ ACQD is a Parallelogram Now, Diagonals of parallelogram ACQD bisect each other ∴ CP = DP and, AP = QP (Given) (AD ∥ BC as opposite sides of parallelogram are parallel) In ∆CPA and ∆DPQ CP = DP ∠CPA = ∠DPQ AP = QP ∴ ∠CPA = ∠DPQ ∴ ar (CPA) = ar (DPQ) From (1) & (2) ar (BPC) = ar (DPQ) Hence Proved (Proved earlier) (Vertically opposite Angles) (Proved earlier) (SAS Congruency) (Area of Congruent triangles is equal) …(2) From (1) & (2) ar (BPC) = ar (DPQ) Hence Proved