Question 2 - Important questions on Parallelograms and Triangles - Areas of Parallelograms and Triangles

Transcript

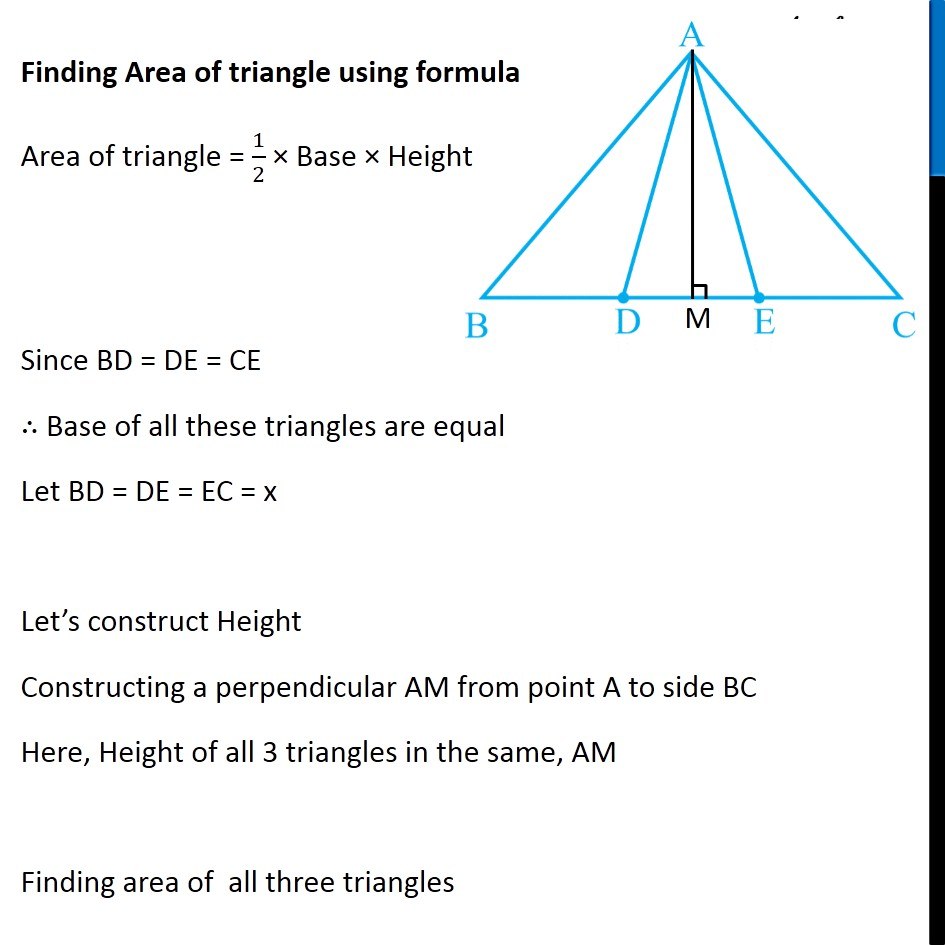
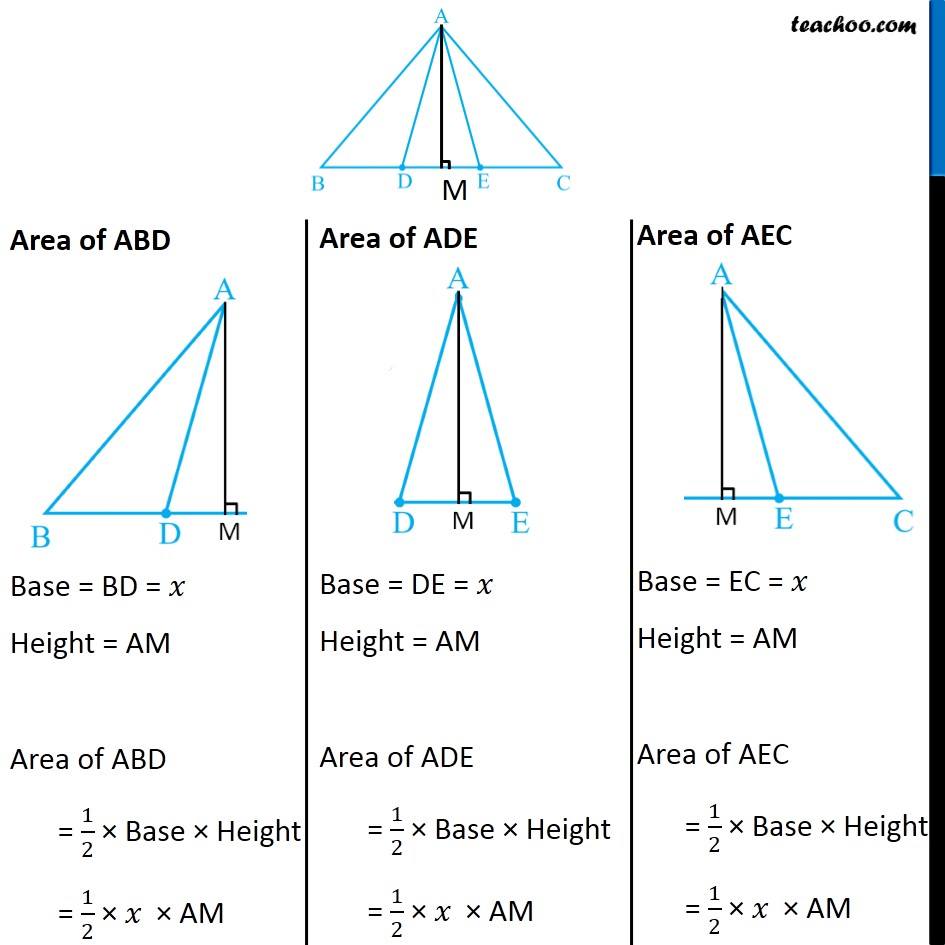
Question 2 In Fig. 9.30, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC). Can you now answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area? [Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex o BC, you can divide ΔABC into n triangles of equal areas.] Finding Area of triangle using formula Area of triangle = 1/2 × Base × Height Since BD = DE = CE ∴ Base of all these triangles are equal Let BD = DE = EC = x Let’s construct Height Constructing a perpendicular AM from point A to side BC Here, Height of all 3 triangles in the same, AM Finding area of all three triangles Area of ABD Base = BD = 𝑥 Height = AM Area of ABD = 1/2 × Base × Height = 1/2 × 𝑥 × AM Area of ADE Base = DE = 𝑥 Height = AM Area of ADE = 1/2 × Base × Height = 1/2 × 𝑥 × AM Area of AEC Base = EC = 𝑥 Height = AM Area of AEC = 1/2 × Base × Height = 1/2 × 𝑥 × AM Thus, Area of ABD = Area of ADE = Area of AEC Hence Proved