Question 8 - Important Questions on Circles - Chapter 9 Class 9 Circles

Transcript

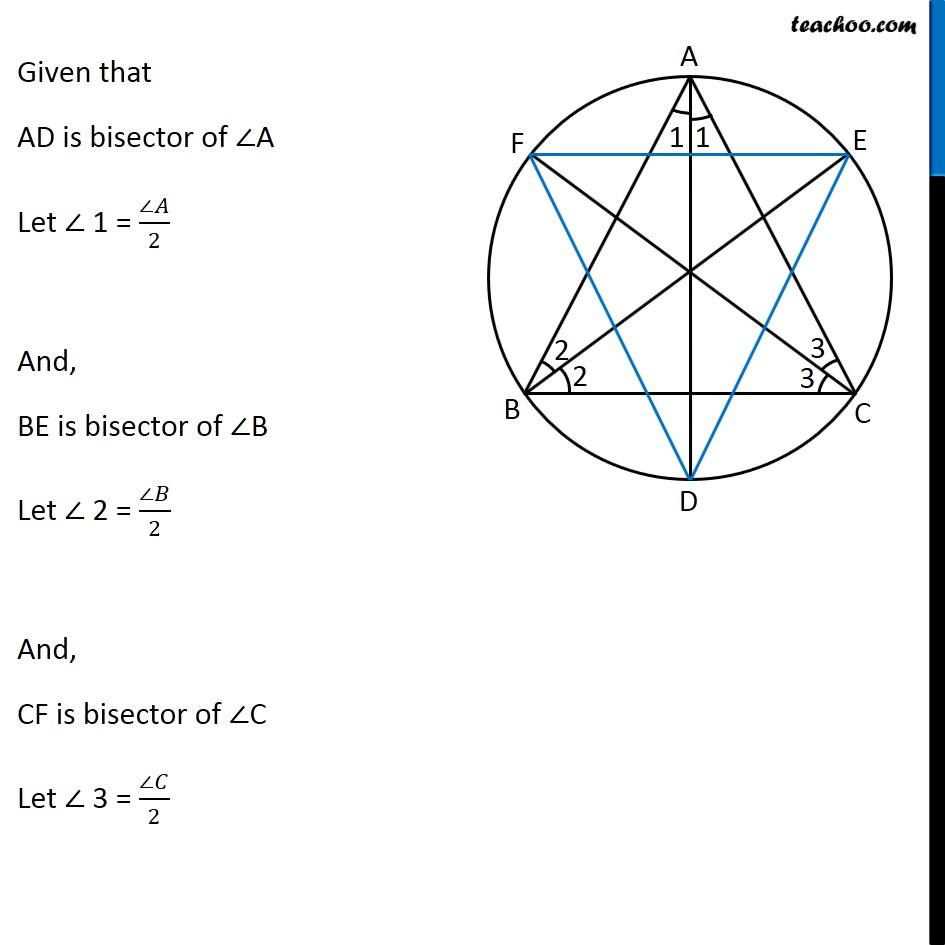
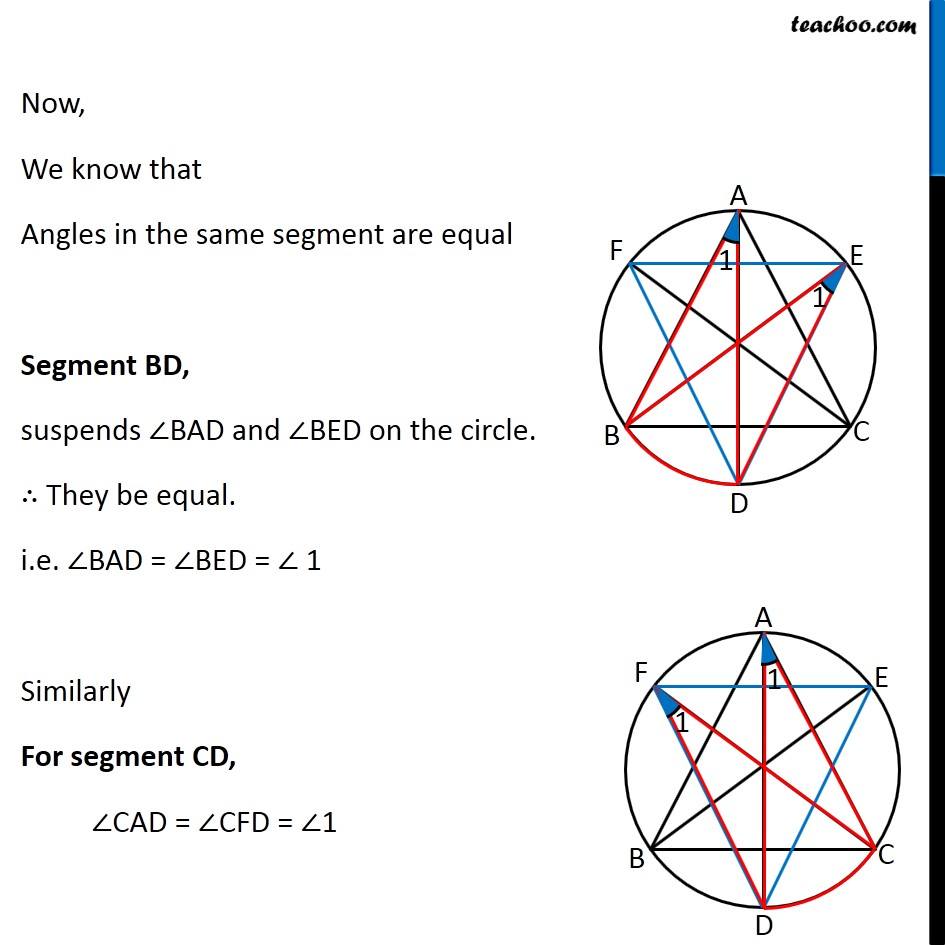
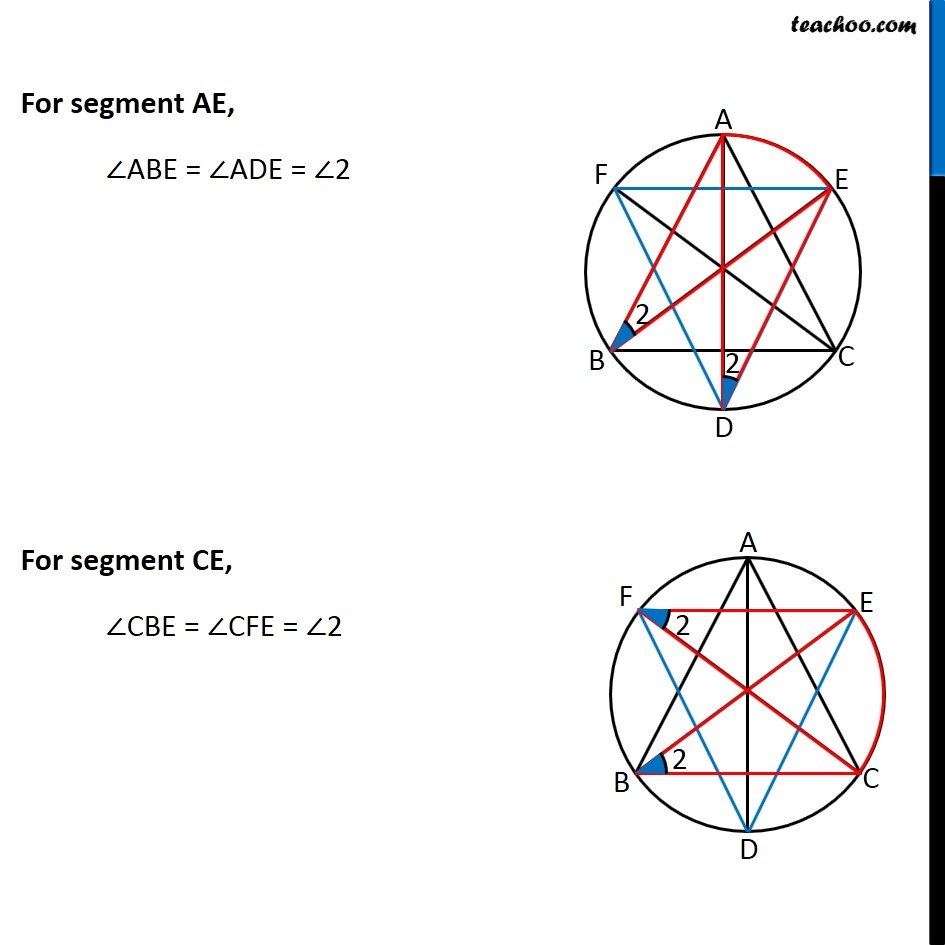
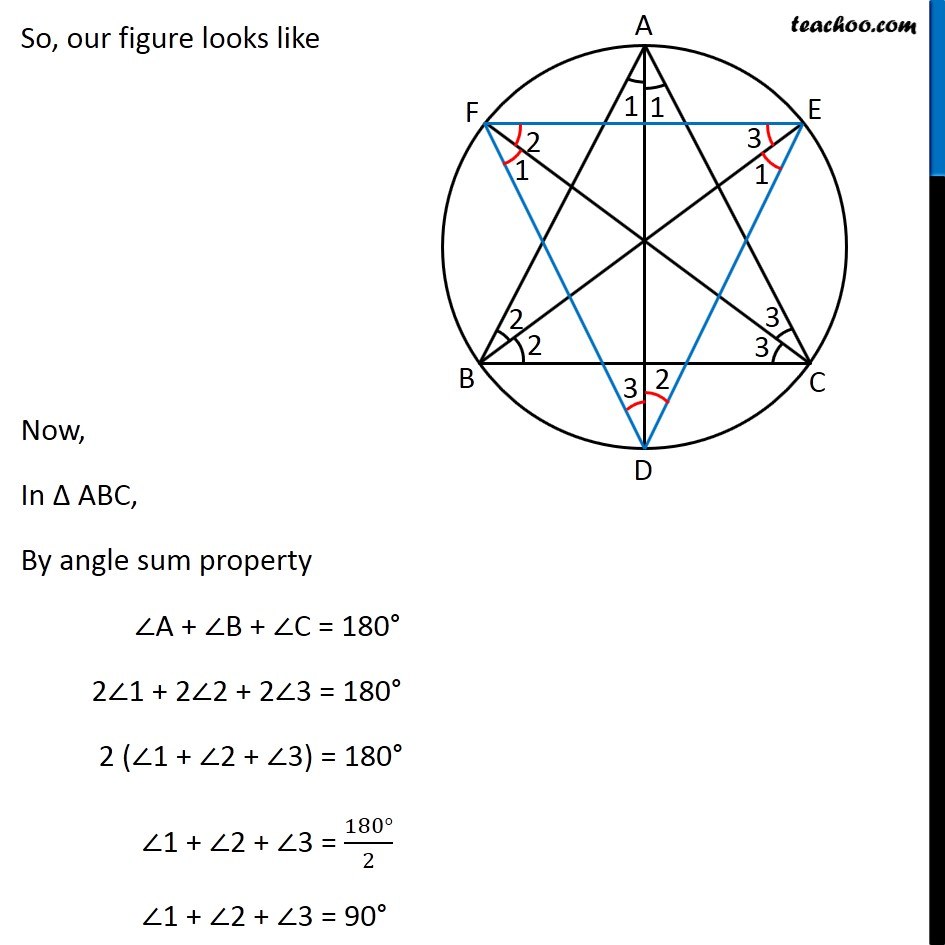
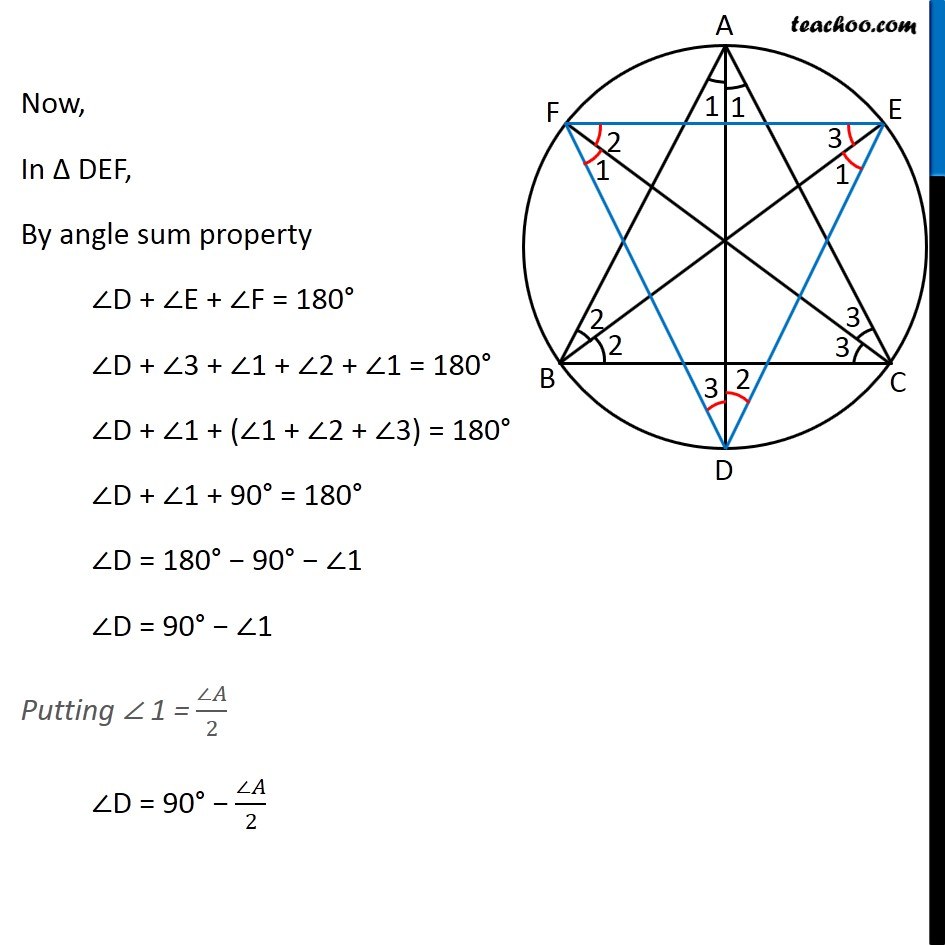
Question 8 Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – 1/2 A, 90° − 1/2 B and 90° − 1/2 C. Circumcircle is a circle where all 3 vertices of triangle are on the circle Given: AD, BE and CF are bisector of angles A, B and C of ∆ABC To Prove: Angles of ∆DEF are 90° − 1/2 ∠ A, 90° − 1/2 ∠B and 90° − 1/2 ∠C Proof: Given that AD is bisector of ∠A Let ∠ 1 = (∠𝐴)/2 And, BE is bisector of ∠B Let ∠ 2 = (∠𝐵)/2 And, CF is bisector of ∠C Let ∠ 3 = (∠𝐶)/2 Now, We know that Angles in the same segment are equal Segment BD, suspends ∠BAD and ∠BED on the circle. ∴ They be equal. i.e. ∠BAD = ∠BED = ∠ 1 Similarly For segment CD, ∠CAD = ∠CFD = ∠1 For segment AE, ∠ABE = ∠ADE = ∠2 For segment CE, ∠CBE = ∠CFE = ∠2 For segment AF ∠ACF = ∠ADF = ∠3 For segment FB ∠FCB = ∠FEB = ∠3 So, our figure looks like Now, In Δ ABC, By angle sum property ∠A + ∠B + ∠C = 180° 2∠1 + 2∠2 + 2∠3 = 180° 2 (∠1 + ∠2 + ∠3) = 180° ∠1 + ∠2 + ∠3 = (180°)/2 ∠1 + ∠2 + ∠3 = 90° Now, In Δ DEF, By angle sum property ∠D + ∠E + ∠F = 180° ∠D + ∠3 + ∠1 + ∠2 + ∠1 = 180° ∠D + ∠1 + (∠1 + ∠2 + ∠3) = 180° ∠D + ∠1 + 90° = 180° ∠D = 180° − 90° − ∠1 ∠D = 90° − ∠1 Putting ∠ 1 = (∠𝐴)/2 ∠D = 90° − (∠𝐴)/2 Similarly, we can prove ∠E = 90° − (∠𝐵)/2 ∠F = 90° − (∠𝐶)/2 Hence Proved