Question 6 - Important Questions on Circles - Chapter 9 Class 9 Circles

Transcript

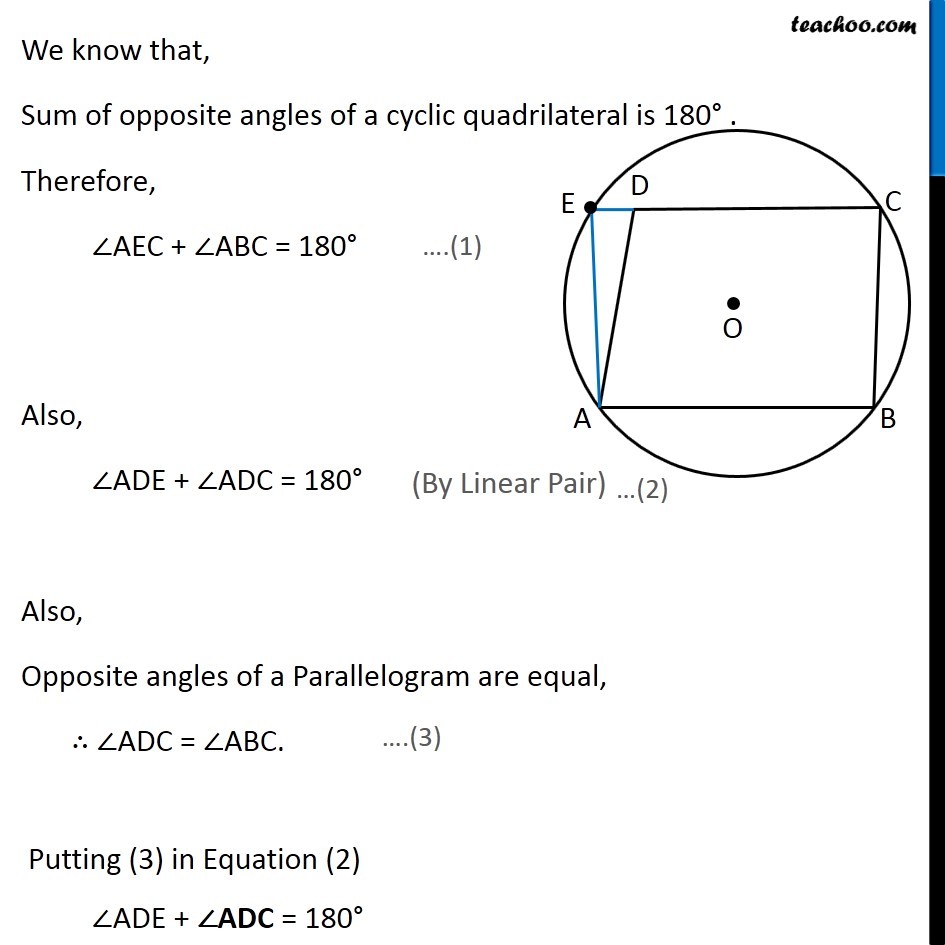
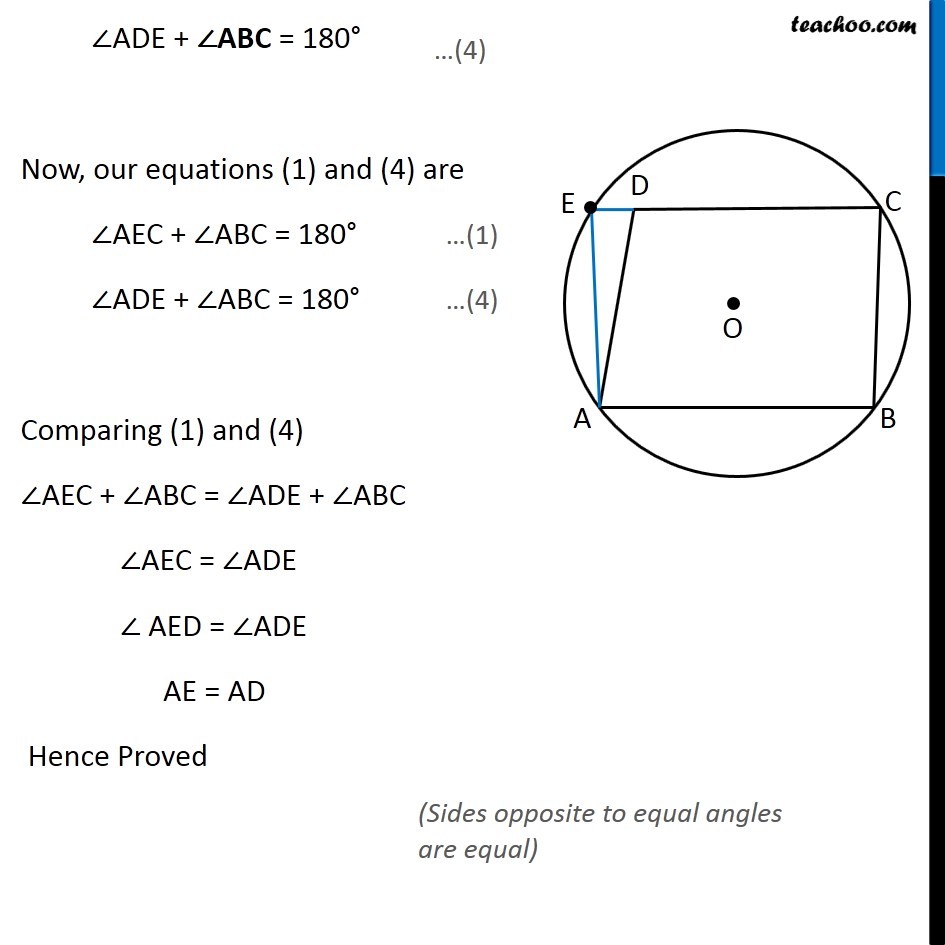
Question 6 ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD . Given: A Parallelogram ABCD a circle is drawn through A, B and C which intersects CD Produced at E. To Prove: AE = AD Construction: Join AE Proof: Since points A, B, C, E lie on a circle ∴ ABCE is a cyclic quadrilateral. We know that, Sum of opposite angles of a cyclic quadrilateral is 180° . Therefore, ∠AEC + ∠ABC = 180° Also, ∠ADE + ∠ADC = 180° Also, Opposite angles of a Parallelogram are equal, ∴ ∠ADC = ∠ABC. Putting (3) in Equation (2) ∠ADE + ∠ADC = 180° (By Linear Pair) ∠ADE + ∠ABC = 180° Now, our equations (1) and (4) are ∠AEC + ∠ABC = 180° …(1) ∠ADE + ∠ABC = 180° …(4) Comparing (1) and (4) ∠AEC + ∠ABC = ∠ADE + ∠ABC ∠AEC = ∠ADE ∠ AED = ∠ADE AE = AD Hence Proved (Sides opposite to equal angles are equal)