Question 4 - Important Questions on Circles - Chapter 9 Class 9 Circles

Transcript

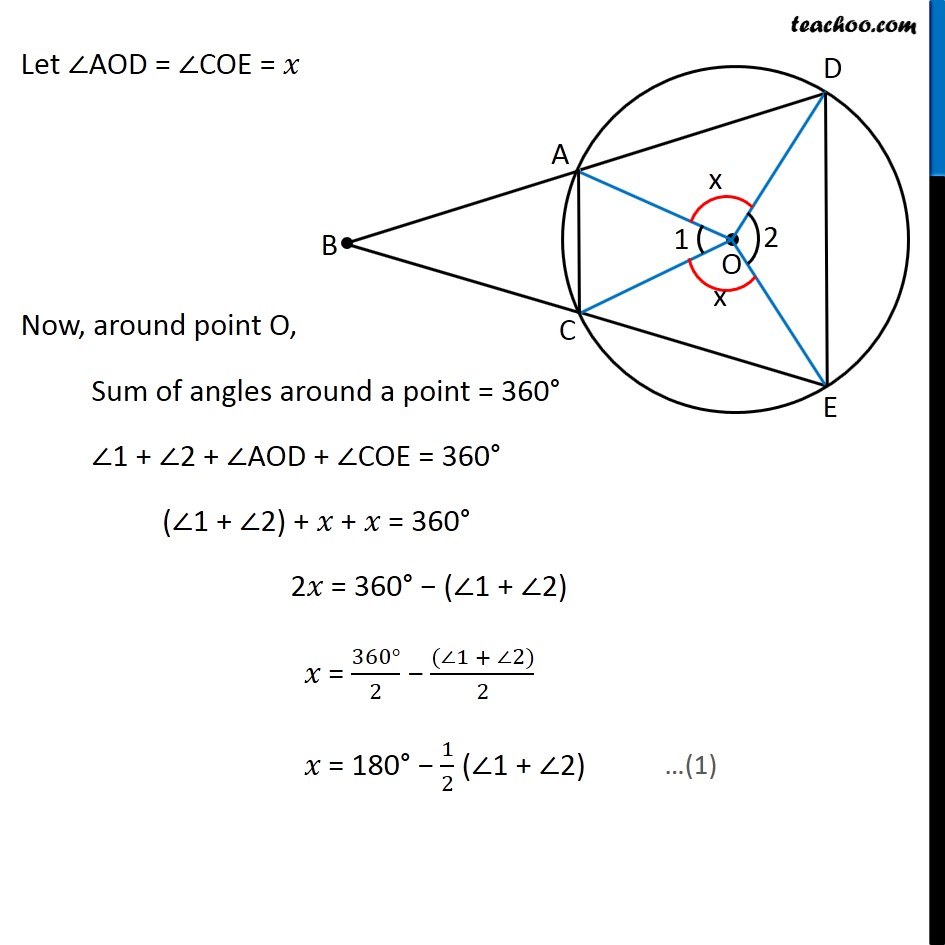
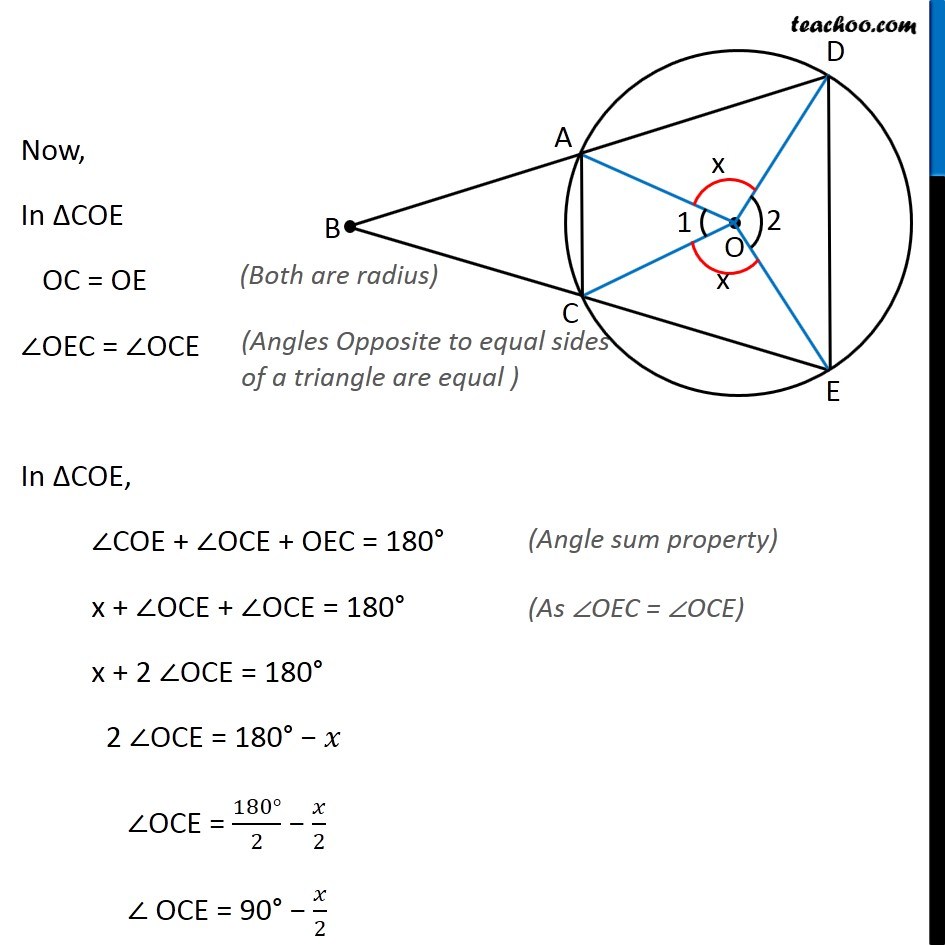
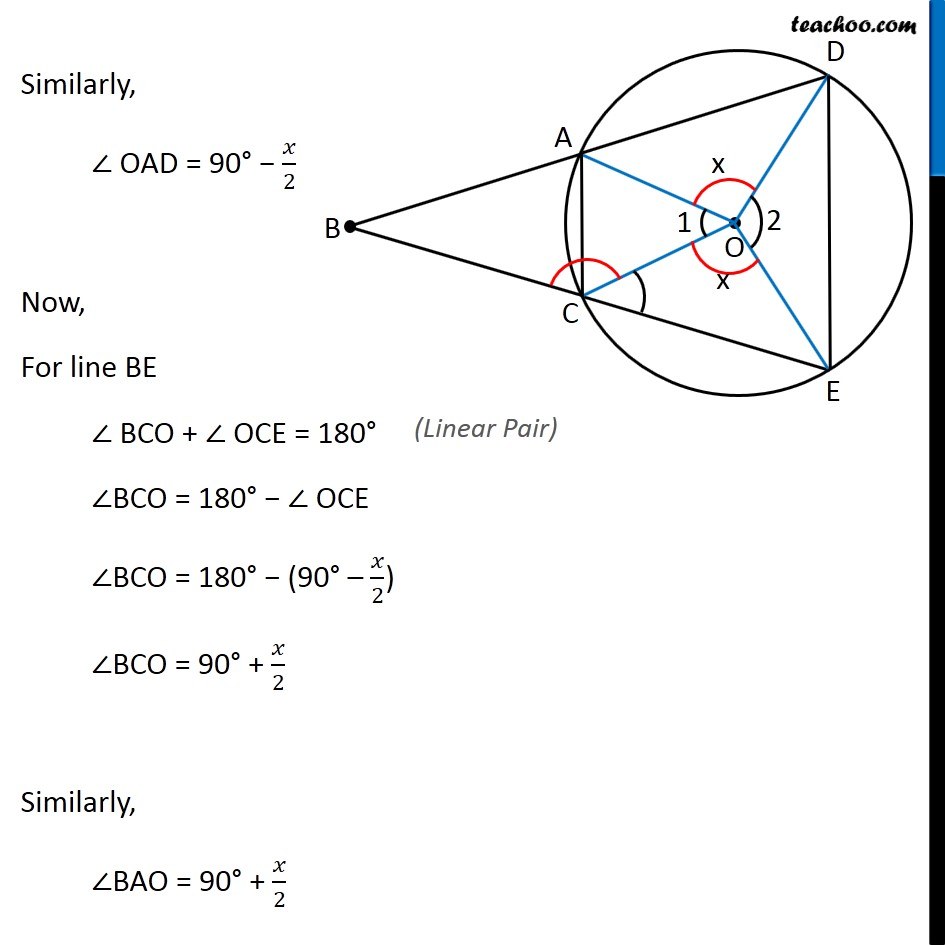
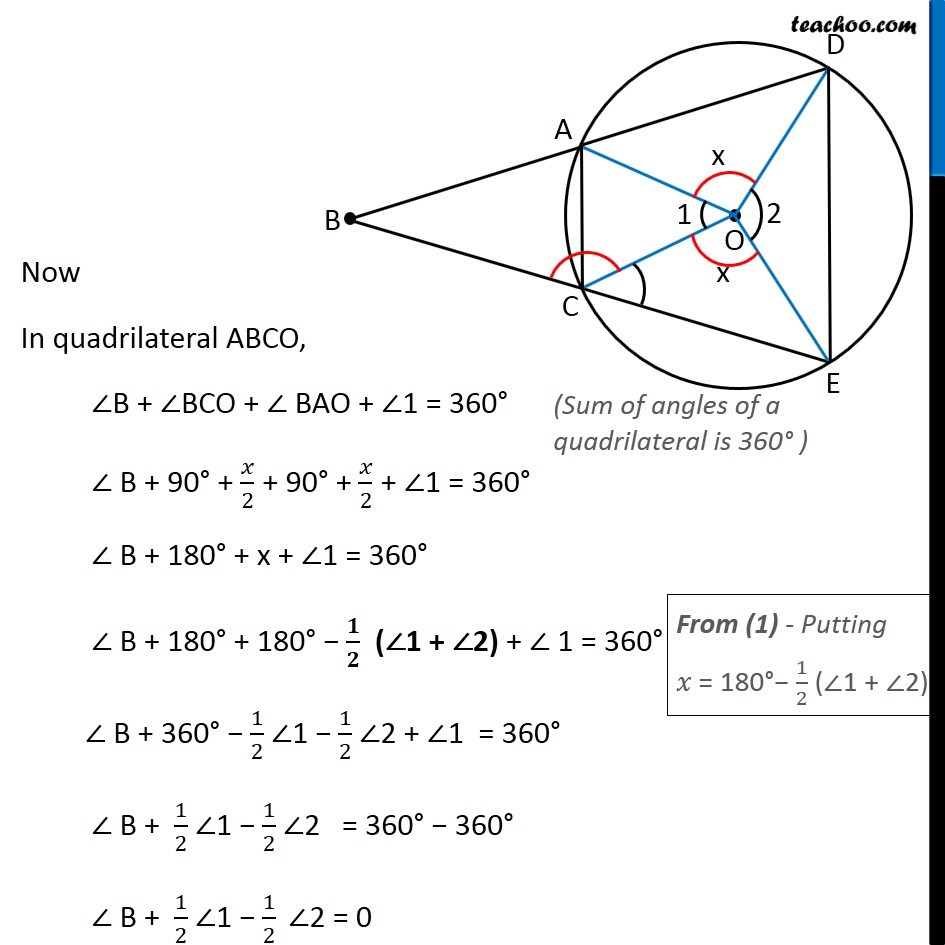
Question 4 – Method 1 Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the center. Given: Equal chords AD and CE To Prove: ∠ABC = 1/2 (∠AOC − ∠DOE) Construction: Join AC and DE Proof: Given, AD = CE ∴ ∠AOD = ∠COE (Equal chords subtend equal angle at the center) Let ∠AOD = ∠COE = 𝑥 Now, around point O, Sum of angles around a point = 360° ∠1 + ∠2 + ∠AOD + ∠COE = 360° (∠1 + ∠2) + 𝑥 + 𝑥 = 360° 2𝑥 = 360° − (∠1 + ∠2) 𝑥 = (360°)/2 − ((∠1 + ∠2))/2 𝑥 = 180° − 1/2 (∠1 + ∠2) Now, In ∆COE OC = OE ∠OEC = ∠OCE In ∆COE, ∠COE + ∠OCE + OEC = 180° x + ∠OCE + ∠OCE = 180° x + 2 ∠OCE = 180° 2 ∠OCE = 180° − 𝑥 ∠OCE = (180°)/2 − 𝑥/2 ∠ OCE = 90° − 𝑥/2 (Both are radius) (Angles Opposite to equal sides of a triangle are equal ) (Angle sum property) (As ∠OEC = ∠OCE) Similarly, ∠ OAD = 90° − 𝑥/2 Now, For line BE ∠ BCO + ∠ OCE = 180° ∠BCO = 180° − ∠ OCE ∠BCO = 180° − (90° – 𝑥/2) ∠BCO = 90° + 𝑥/2 Similarly, ∠BAO = 90° + 𝑥/2 (Linear Pair) Now In quadrilateral ABCO, ∠B + ∠BCO + ∠ BAO + ∠1 = 360° ∠ B + 90° + 𝑥/2 + 90° + 𝑥/2 + ∠1 = 360° ∠ B + 180° + x + ∠1 = 360° ∠ B + 180° + 180° − 𝟏/𝟐 (∠1 + ∠2) + ∠ 1 = 360° ∠ B + 360° − 1/2 ∠1 − 1/2 ∠2 + ∠1 = 360° ∠ B + 1/2 ∠1 − 1/2 ∠2 = 360° − 360° ∠ B + 1/2 ∠1 − 1/2 ∠2 = 0 (Sum of angles of a quadrilateral is 360° ) From (1) - Putting 𝑥 = 180°− 1/2 (∠1 + ∠2) ∠ B = 1/2 ∠2 − 1/2 ∠1 ∠B = 1/2 (∠2 − ∠1) Hence Proved Question 4 – Method 2 Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the center. Given: Equal chords AD and CE To Prove: ∠ABC = 1/2 (∠AOC − ∠DOE) Construction: Join AC, DE and AE, DC Proof: We know that, Angle subtended by arc at the center is double angle subtended by it at any other point For arc DE Angle subtended at the center = ∠ DOE = ∠ 2 …(1) Angle subtended on circle = ∠ DCE ∴ ∠ DCE = (∠ 2)/2 For arc AC Angle subtended at the center = ∠ AOC = ∠ 1 Angle subtended on circle = ∠ AEC ∴ ∠ AEC = (∠ 1)/2 …(2) In Δ ABE Exterior angle is equal to sum of interior opposite angles ∴ ∠ DAE = ∠ ABC + ∠ AEC ∴ ∠ DAE = ∠ ABC + (∠1)/2 Also, ∠ DCE = ∠ DAE So, our equation becomes ∠ DCE = ∠ ABC + (∠1)/2 (∠2)/2 = ∠ ABC + (∠1)/2 (∠2)/2 – (∠1)/2 = ∠ ABC (Angles subtended by a chord on same side of triangle are equal) (From (1): ∠ DCE = (∠ 2)/2) 1/2 (∠2 – ∠1) = ∠ ABC 1/2 (∠ AOC – ∠ DOE) = ∠ ABC Hence proved