Ex 9.1, 11 - Chapter 9 Class 8 Mensuration

Transcript

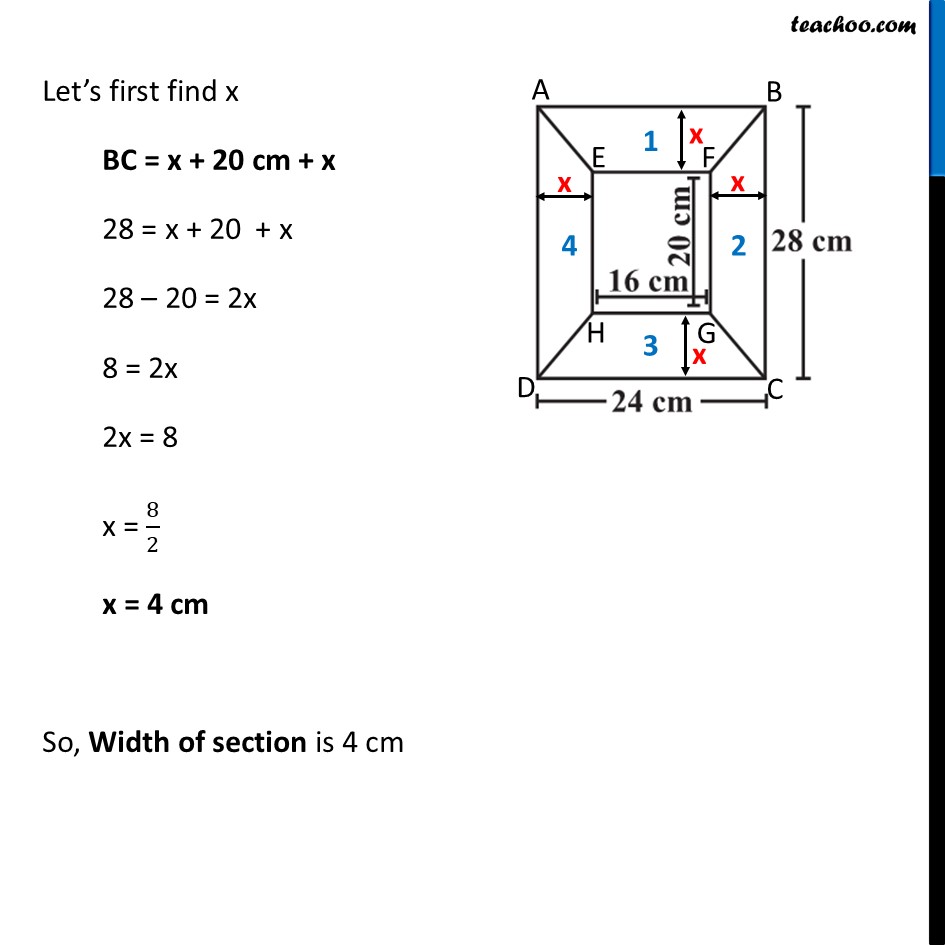
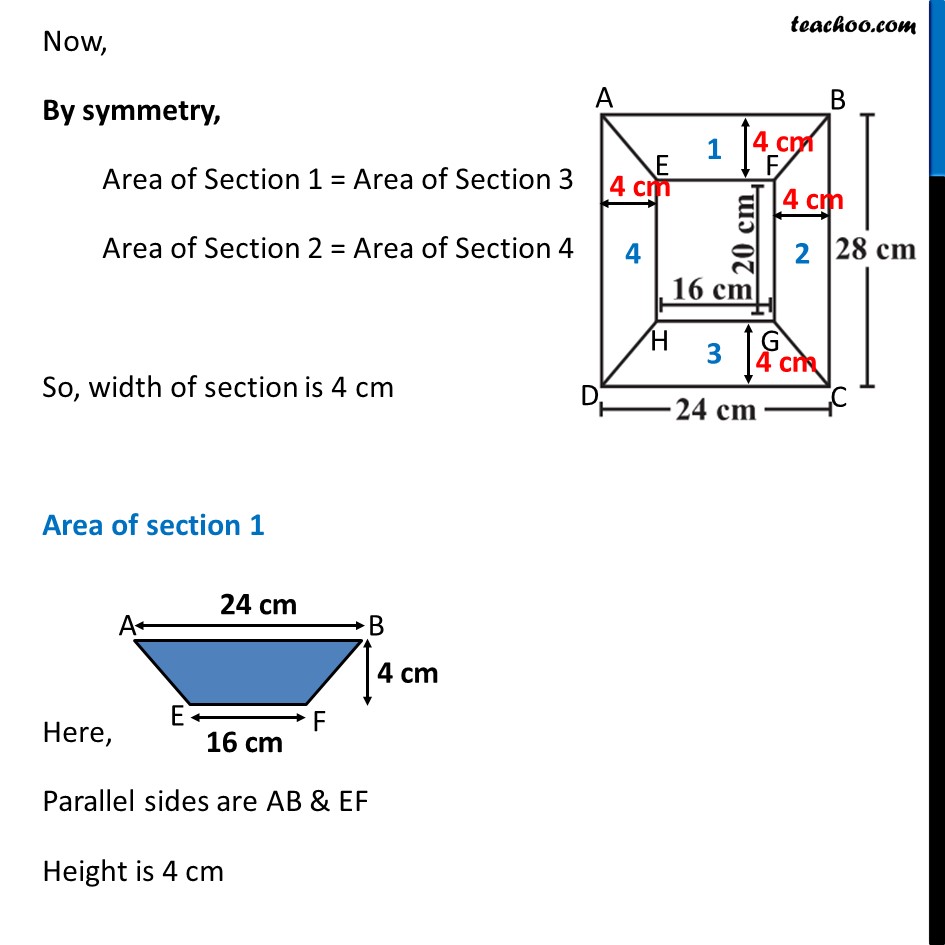
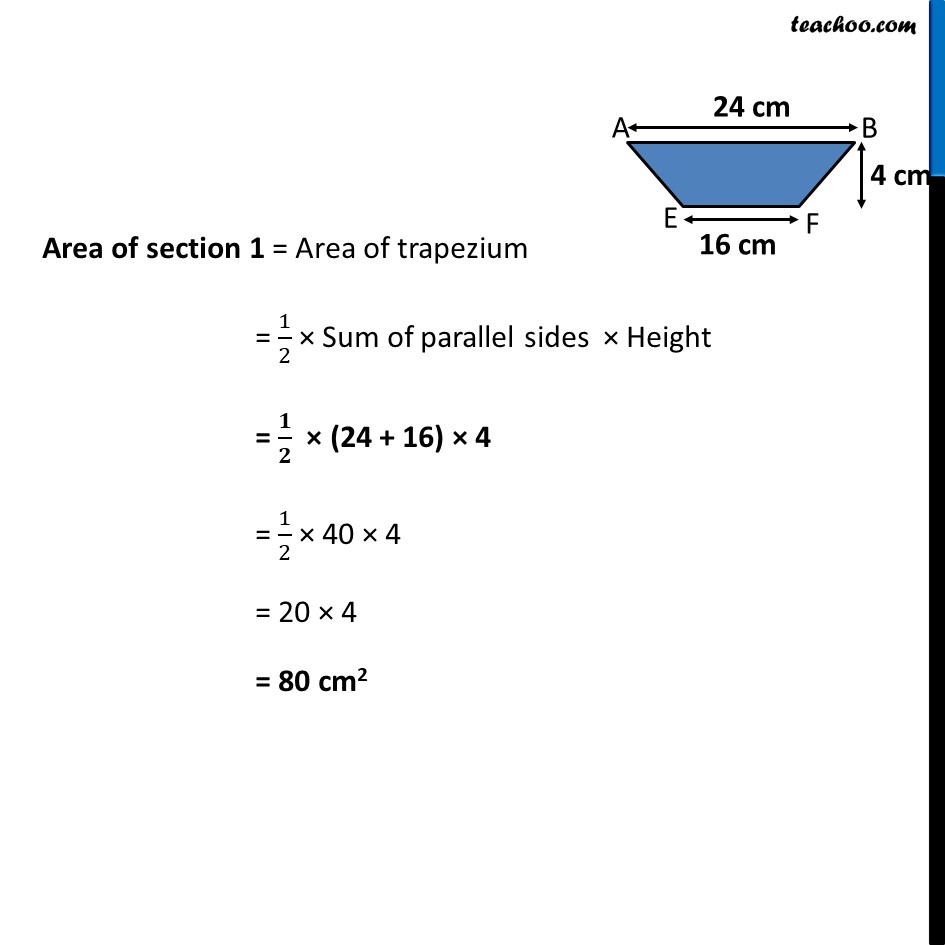
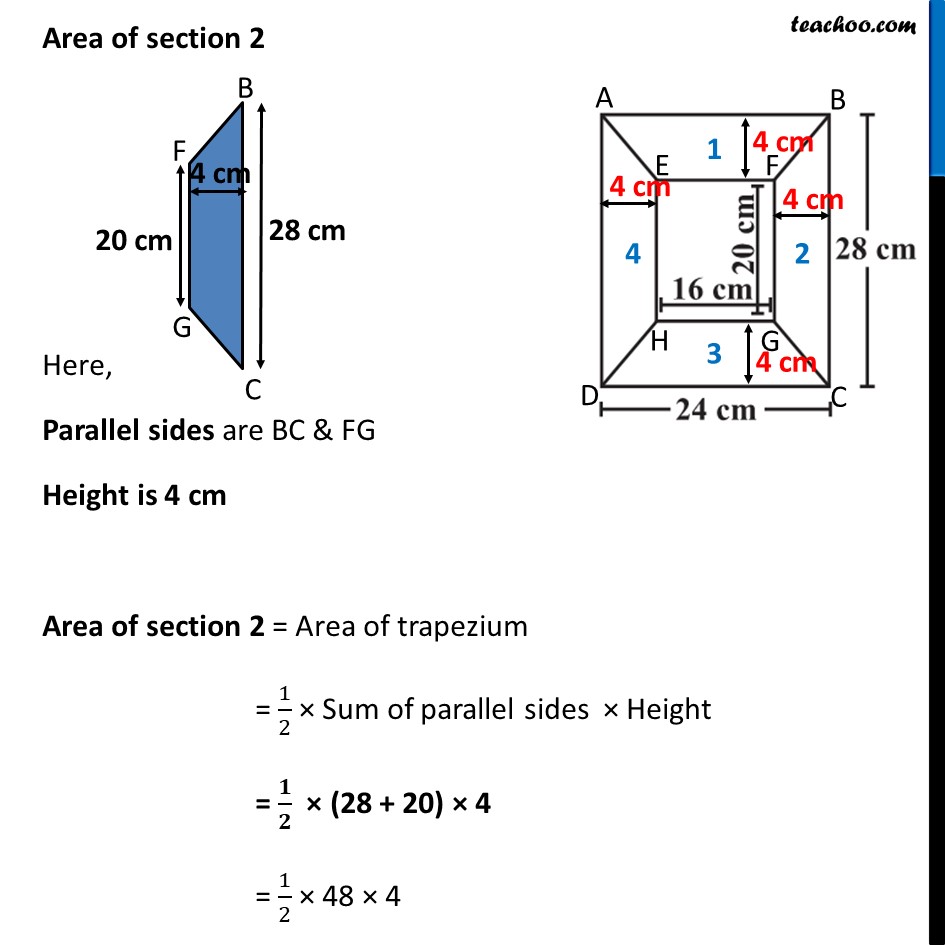
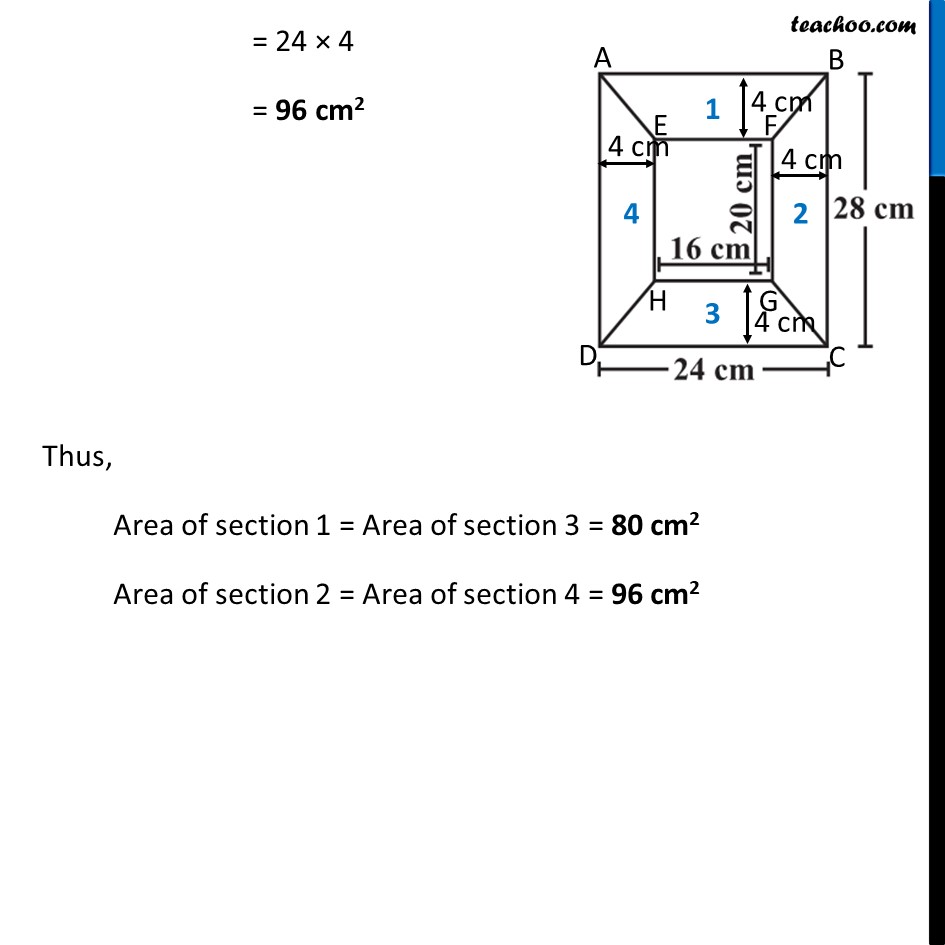
Ex 9.1, 11 Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same. The picture frame has 4 sections marked as 1 , 2 , 3 and 4 Given that width of each section is same Let Width of section = x cm Let’s first find x BC = x + 20 cm + x 28 = x + 20 + x 28 – 20 = 2x 8 = 2x 2x = 8 x = 8/2 x = 4 cm So, Width of section is 4 cm Now, By symmetry, Area of Section 1 = Area of Section 3 Area of Section 2 = Area of Section 4 So, width of section is 4 cm Area of section 1 Here, Parallel sides are AB & EF Height is 4 cm Area of section 1 = Area of trapezium = 1/2 × Sum of parallel sides × Height = 𝟏/𝟐 × (24 + 16) × 4 = 1/2 × 40 × 4 = 20 × 4 = 80 cm2 Area of section 2 Here, Parallel sides are BC & FG Height is 4 cm Area of section 2 = Area of trapezium = 1/2 × Sum of parallel sides × Height = 𝟏/𝟐 × (28 + 20) × 4 = 1/2 × 48 × 4 = 24 × 4 = 96 cm2 Thus, Area of section 1 = Area of section 3 = 80 cm2 Area of section 2 = Area of section 4 = 96 cm2