Ex 9.1, 10 - Chapter 9 Class 8 Mensuration

Transcript

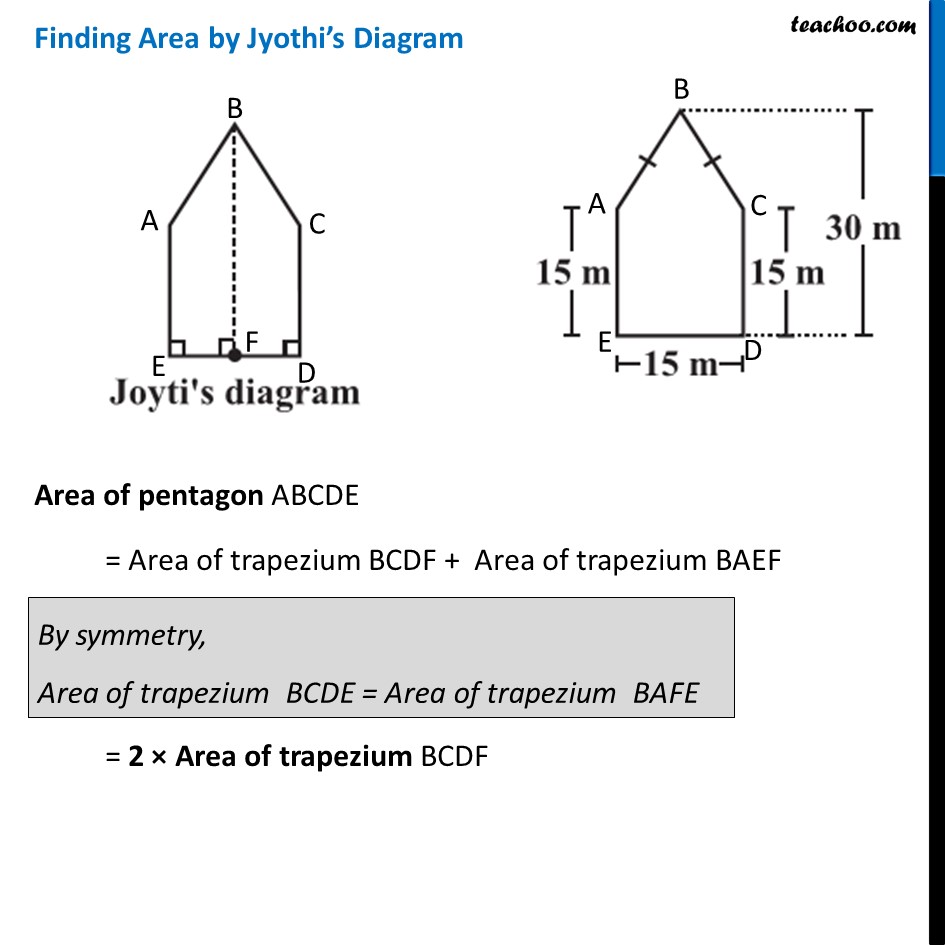
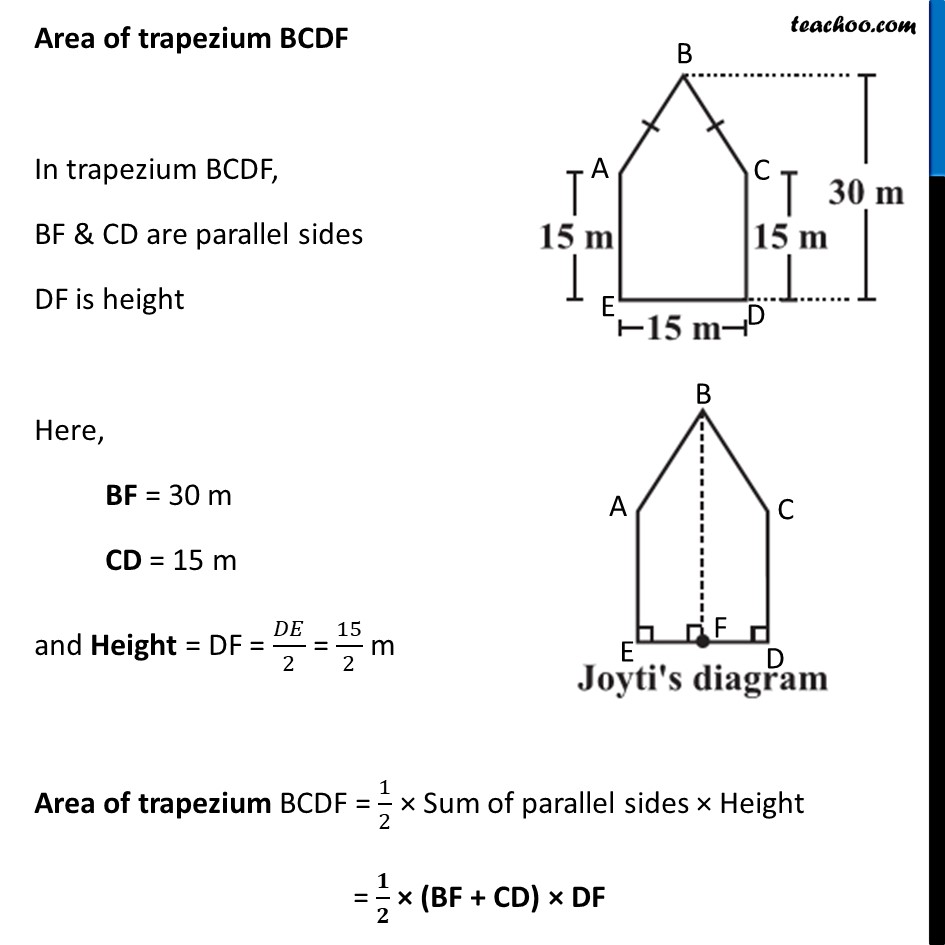
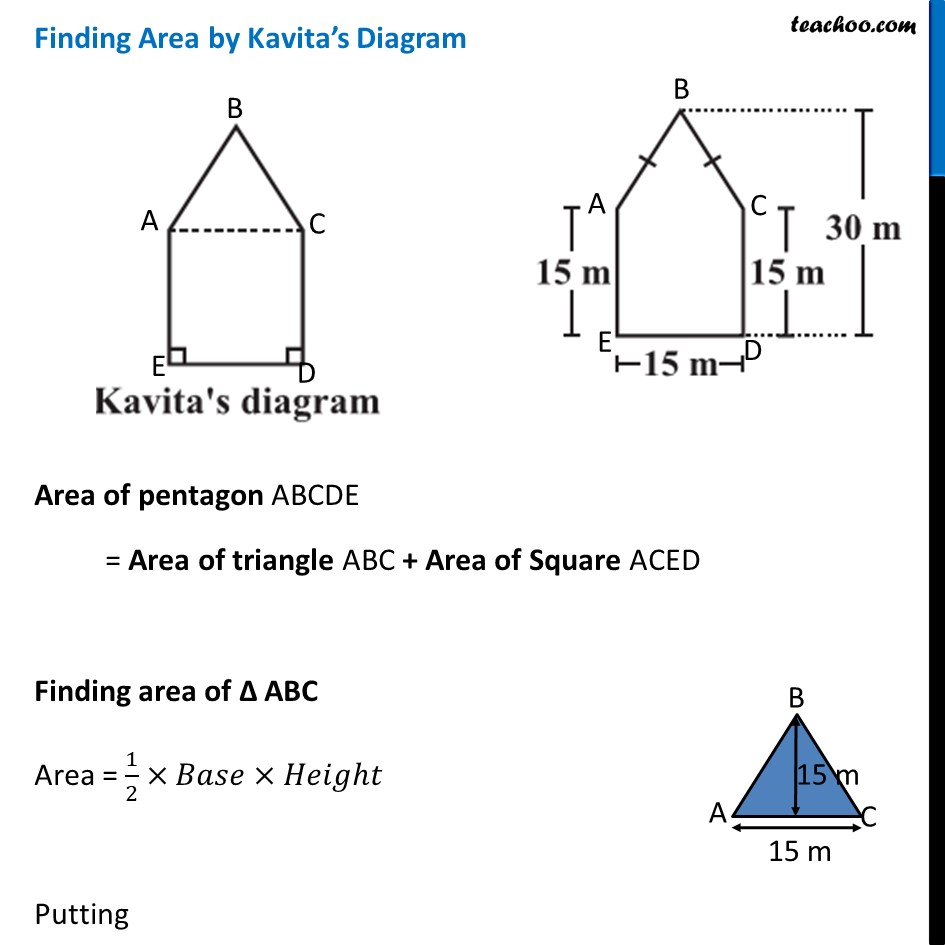
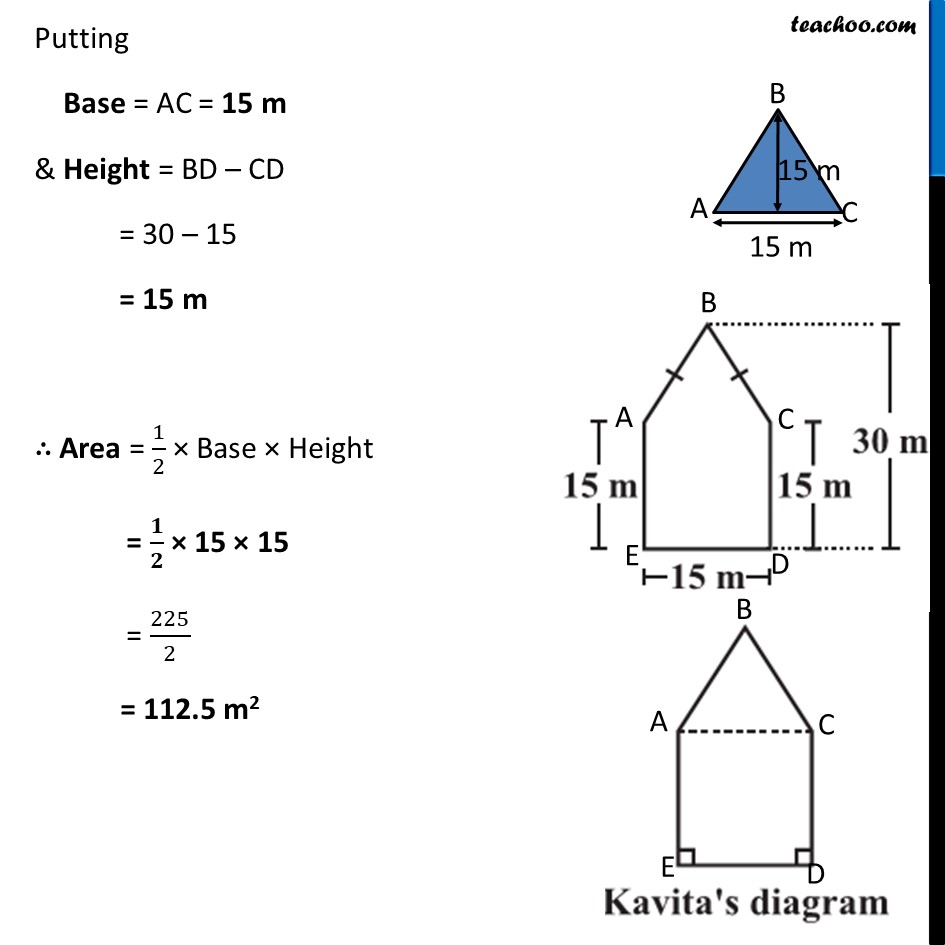
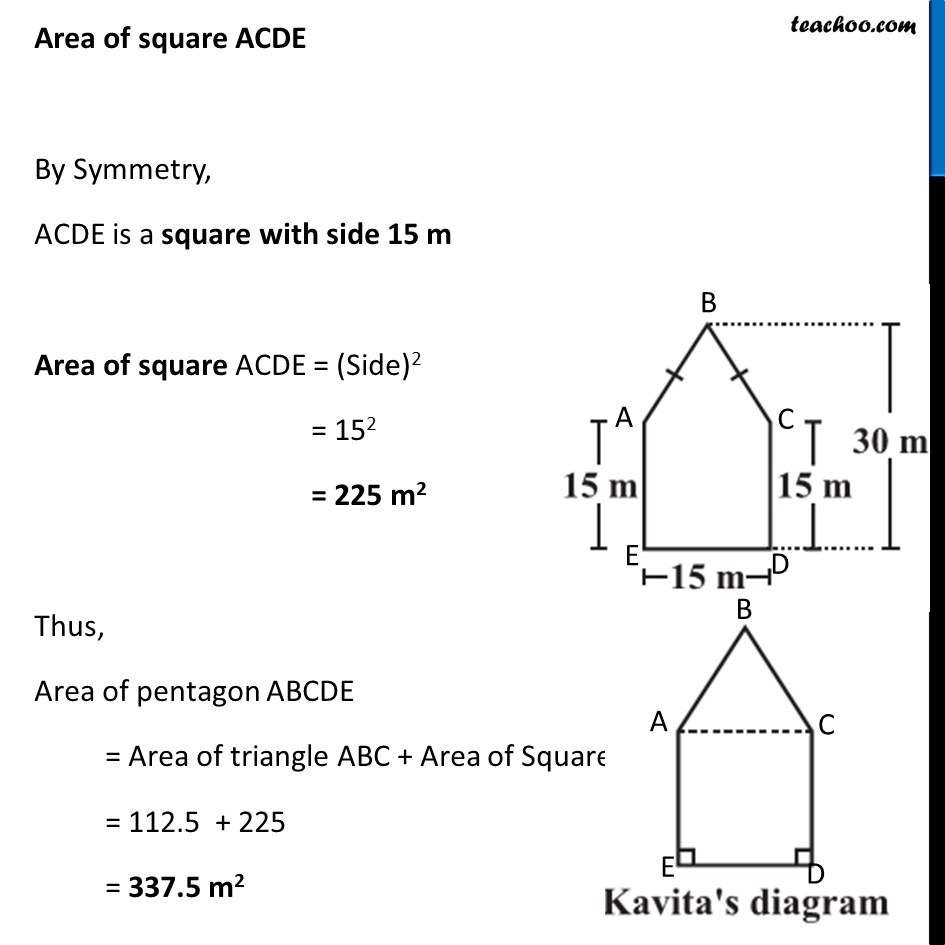
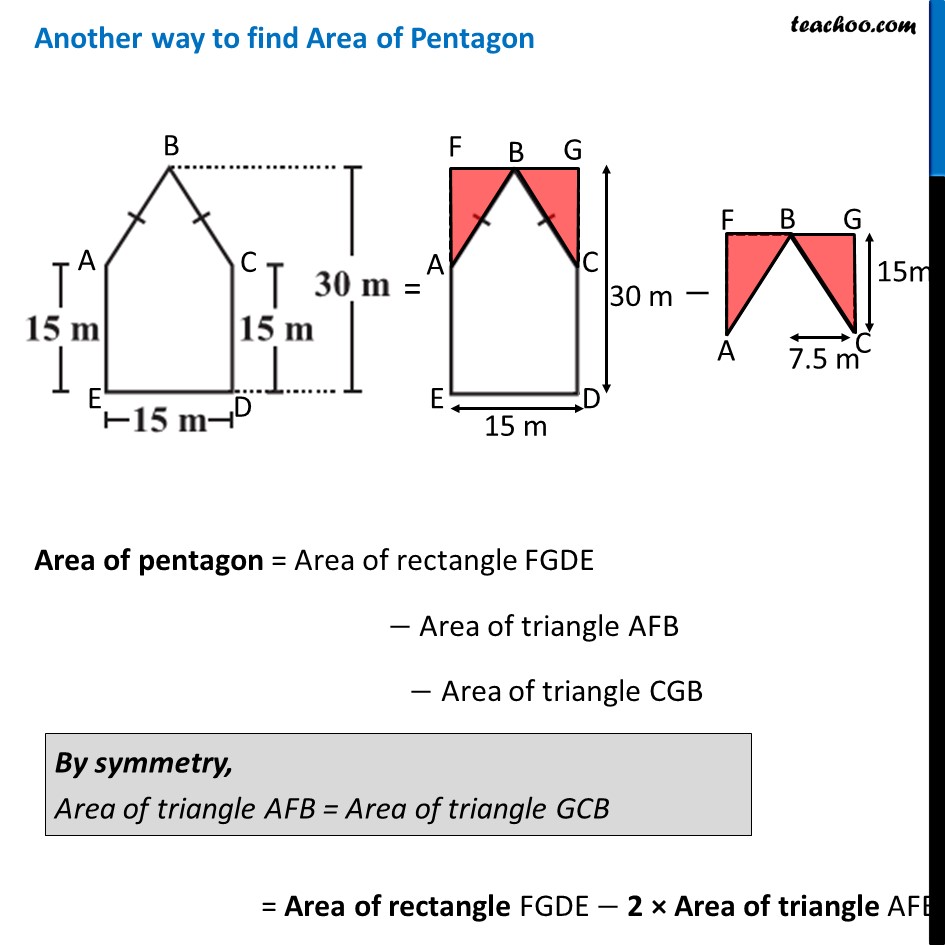
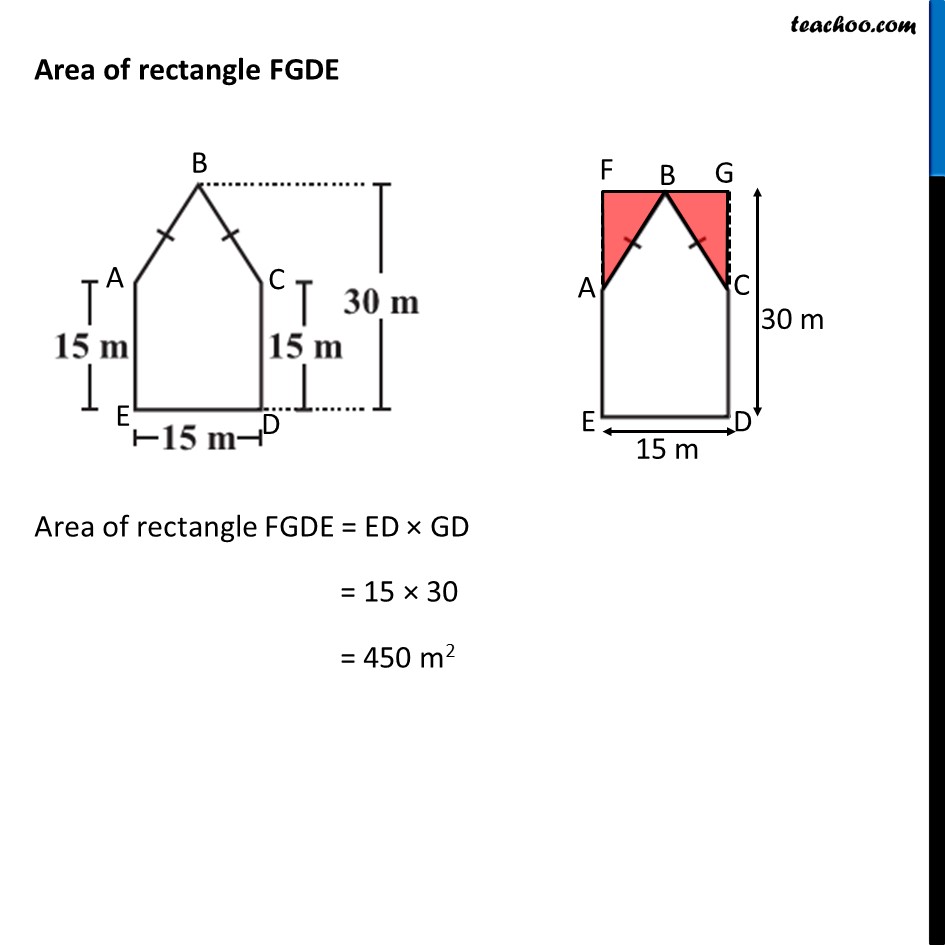
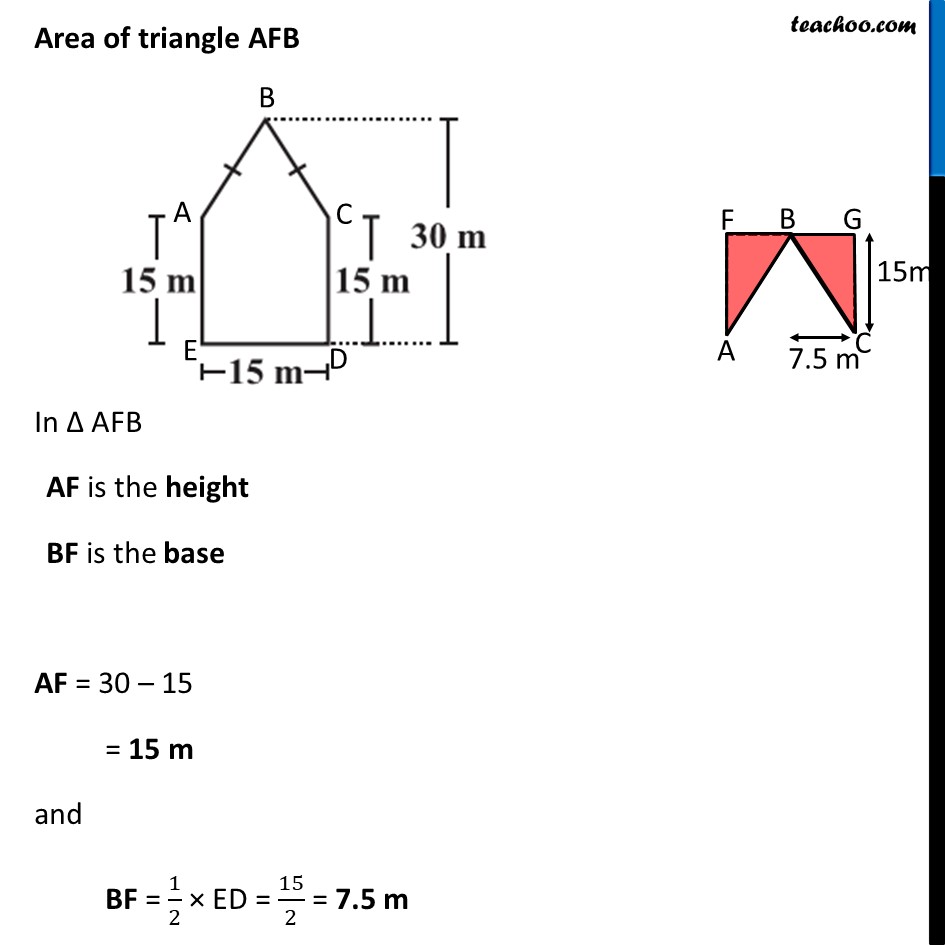
Ex 9.1, 10 There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways. Find the area of this park using both ways. Can you suggest some other way of finding its area? Finding Area by Jyothi’s Diagram Area of pentagon ABCDE = Area of trapezium BCDF + Area of trapezium BAEF = 2 × Area of trapezium BCDF Area of trapezium BCDF In trapezium BCDF, BF & CD are parallel sides DF is height Here, BF = 30 m CD = 15 m and Height = DF = 𝐷𝐸/2 = 15/2 m Area of trapezium BCDF = 1/2 × Sum of parallel sides × Height = 𝟏/𝟐 × (BF + CD) × DF = 1/2 × (30 + 15) × 15/2 = 1/2 × 45 × 15/2 = (45 × 15)/4 Thus, Area of Pentagon ABCDE = 2 × Area of trapezium BCDF = 2 × (45 × 15)/4 = (45 × 15)/2 = 675/2 = 337.5 m2 Finding Area by Kavita’s Diagram Area of pentagon ABCDE = Area of triangle ABC + Area of Square ACED Finding area of ∆ ABC Area = 1/2×𝐵𝑎𝑠𝑒×𝐻𝑒𝑖𝑔ℎ𝑡 Putting Putting Base = AC = 15 m & Height = BD – CD = 30 – 15 = 15 m ∴ Area = 1/2 × Base × Height = 𝟏/𝟐 × 15 × 15 = 225/2 = 112.5 m2 Area of square ACDE By Symmetry, ACDE is a square with side 15 m Area of square ACDE = (Side)2 = 152 = 225 m2 Thus, Area of pentagon ABCDE = Area of triangle ABC + Area of Square ACED = 112.5 + 225 = 337.5 m2 Another way to find Area of Pentagon Area of pentagon = Area of rectangle FGDE − Area of triangle AFB − Area of triangle CGB = Area of rectangle FGDE − 2 × Area of triangle AFB Area of rectangle FGDE Area of rectangle FGDE = ED × GD = 15 × 30 = 450 m2 Area of triangle AFB In Δ AFB AF is the height BF is the base AF = 30 – 15 = 15 m and BF = 1/2 × ED = 15/2 = 7.5 m Area of triangle AFB = 1/2 × BF × AF = 𝟏/𝟐 × 7.5 × 15 Now, Area of pentagon = Area of rectangle FGDE − 2 × Area of triangle AFB = 450 – 2 × 𝟏/𝟐 × 7.5 × 15 = 450 – 7.5 × 15 = 450 – 15/2 × 15 = 450 – 225/2 = 450 – 112.5 = 337.5 m2