

Last updated at December 16, 2024 by Teachoo



Transcript
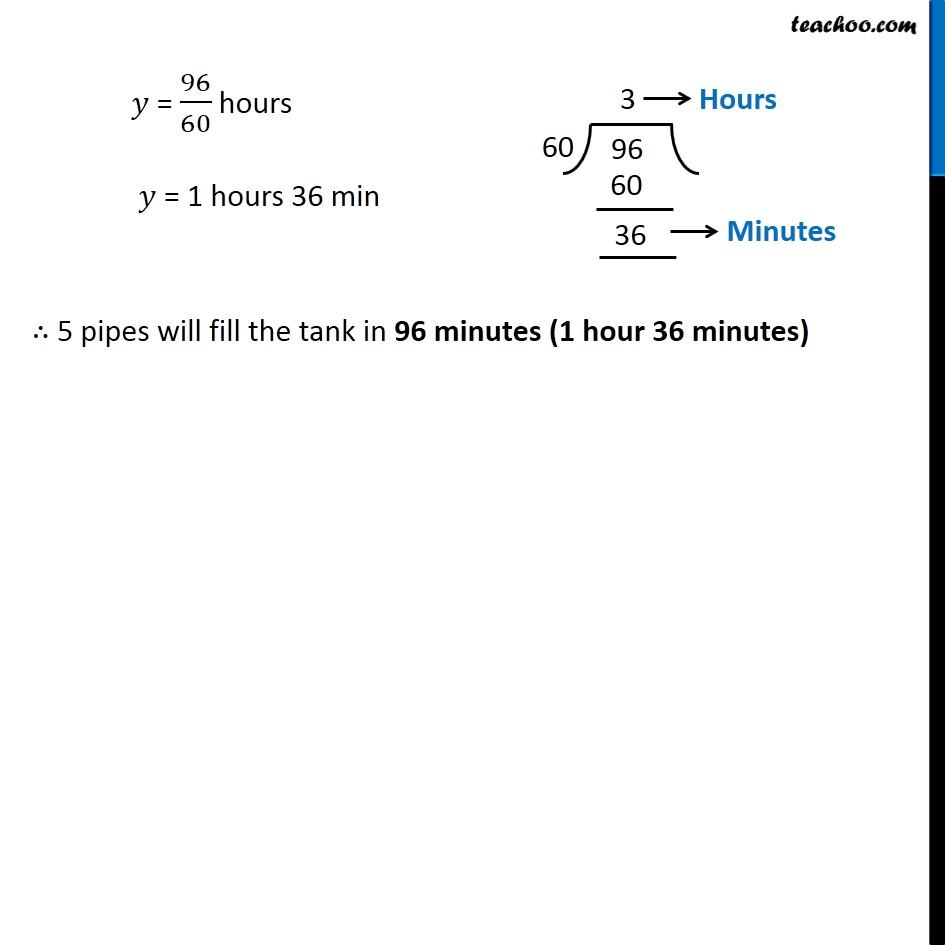
Example 7 6 pipes are required to fill a tank in 1 hour 20 minutes. How long will it take if only 5 pipes of the same type are used? Let’s first convert time into minutes 1 hour 20 minutes = 1 hour + 20 minutes = 60 minutes + 20 minutes = 80 minutes It is given that 6 pipes fill tank in 80 minutes We need to find time taken if 5 pipes are used Let time taken be y minutes Thus, our table looks like As we increase the number of pipes, the time taken to fill the tank decreases ∴ Number of pipes and time taken are in inverse proportion 6 × 80 = 5 × 𝑦 (6 × 80)/5 = 𝑦 6 × 16 = 𝑦 96 = 𝑦 𝑦 = 96 minutes Converting to hours (𝑥1𝑦1=𝑥2𝑦2) 𝑦 = 96/60 hours 𝑦 = 1 hours 36 min ∴ 5 pipes will fill the tank in 96 minutes (1 hour 36 minutes)