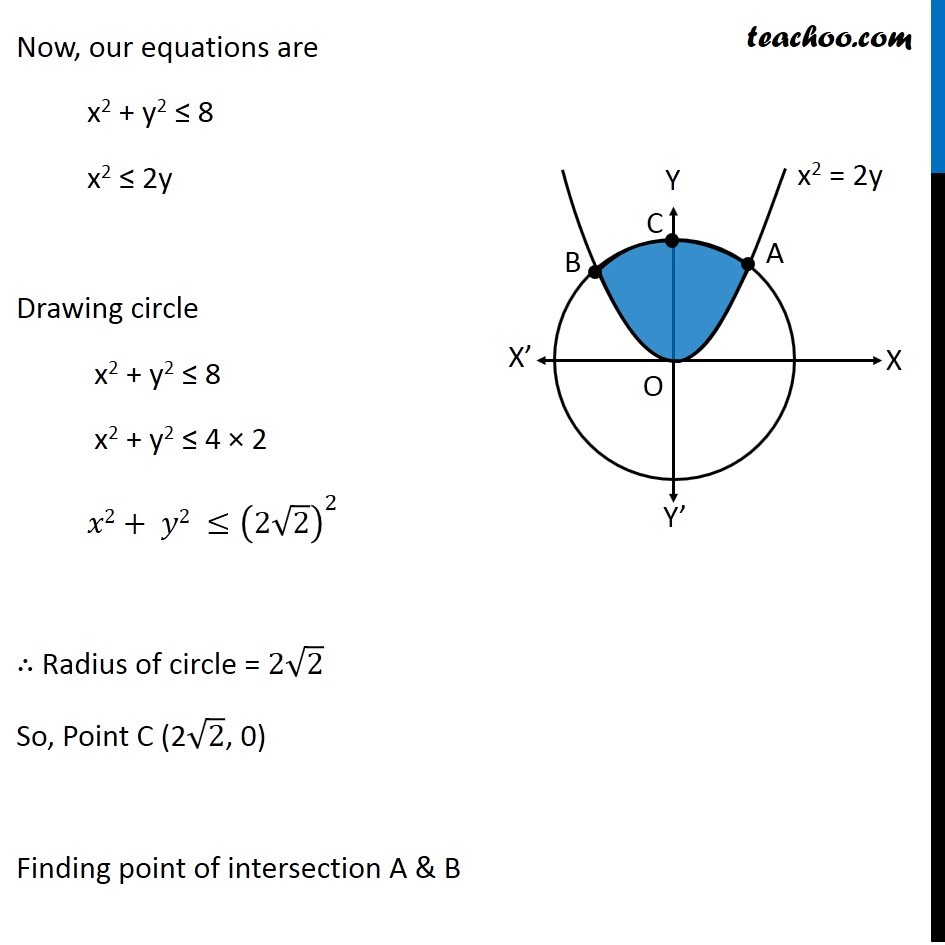
Question 26 (Or 2nd) - CBSE Class 12 Sample Paper for 2019 Boards - Solutions of Sample Papers and Past Year Papers - for Class 12 Boards

Transcript

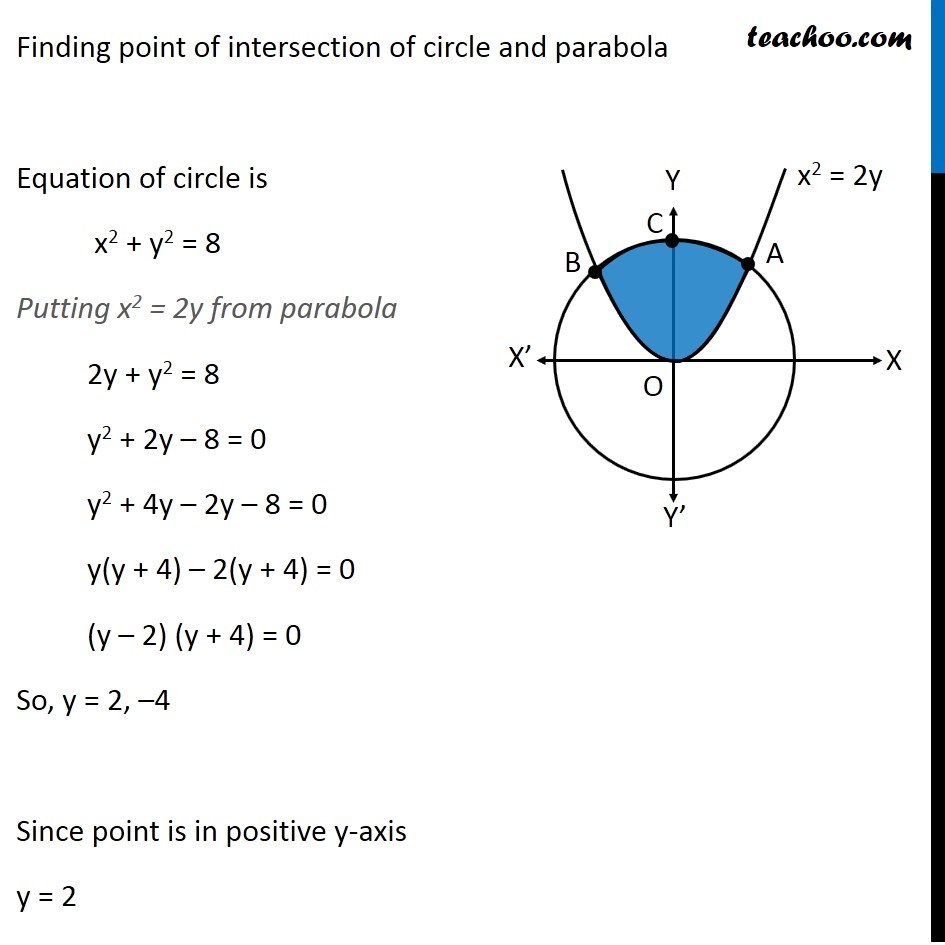
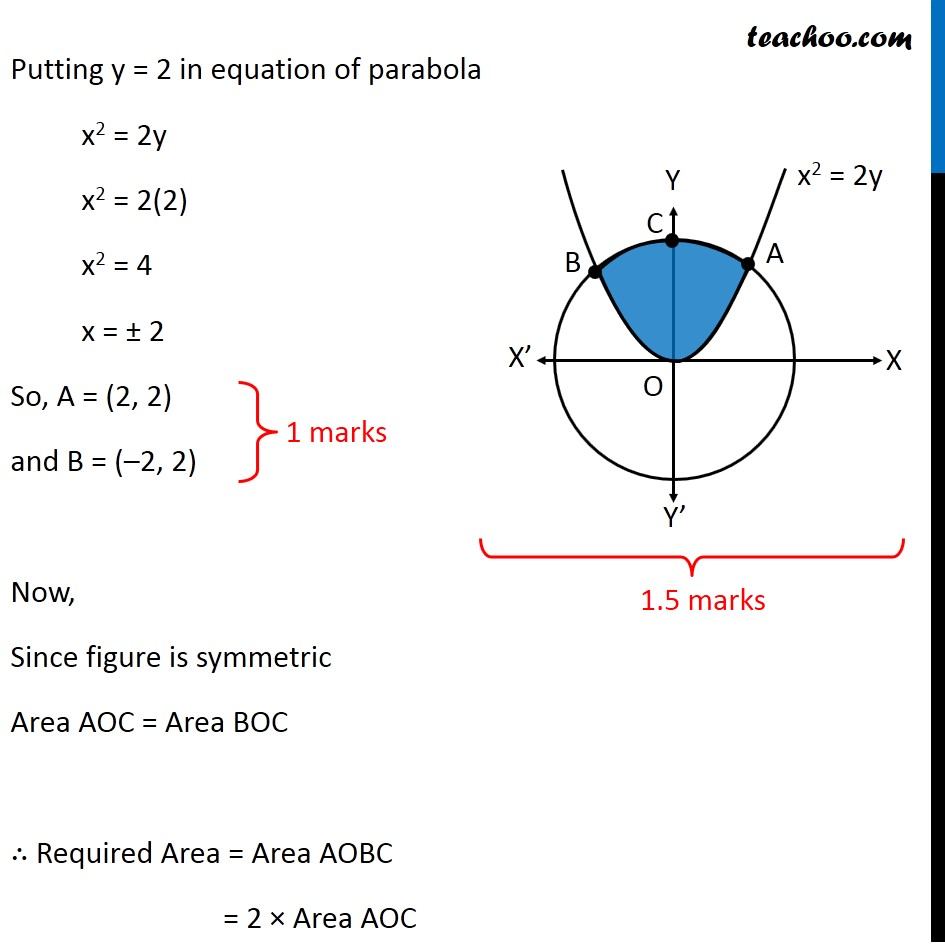
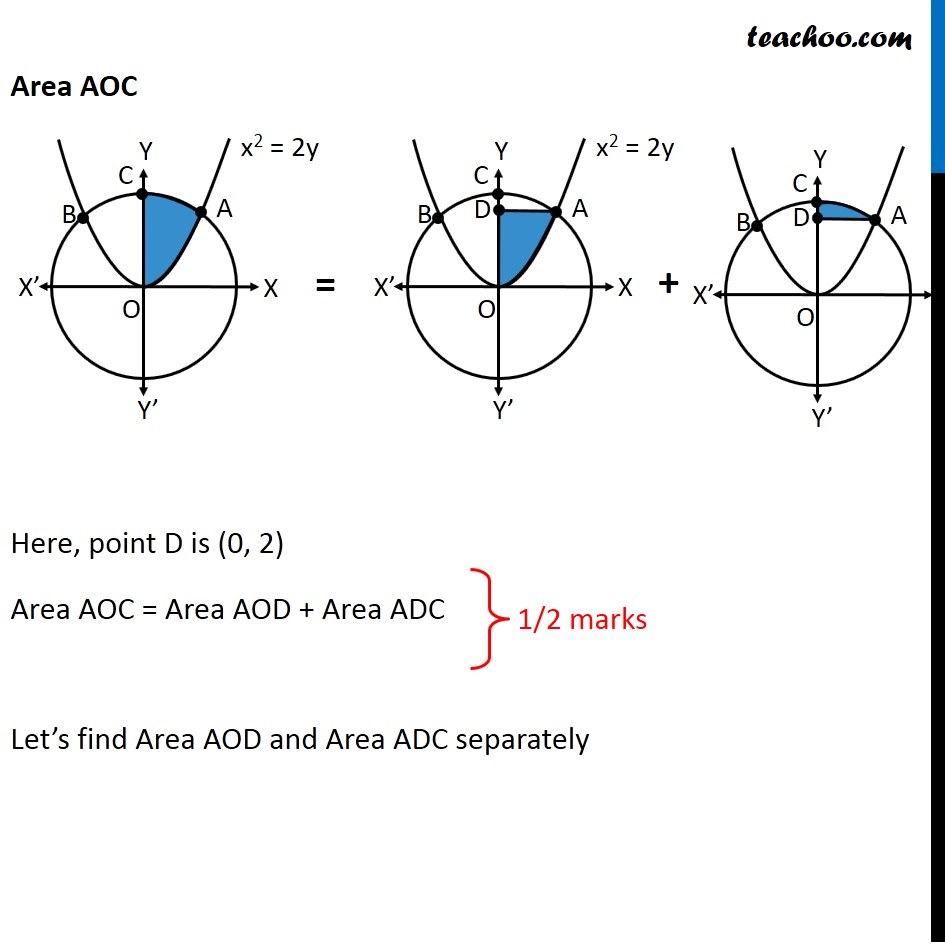
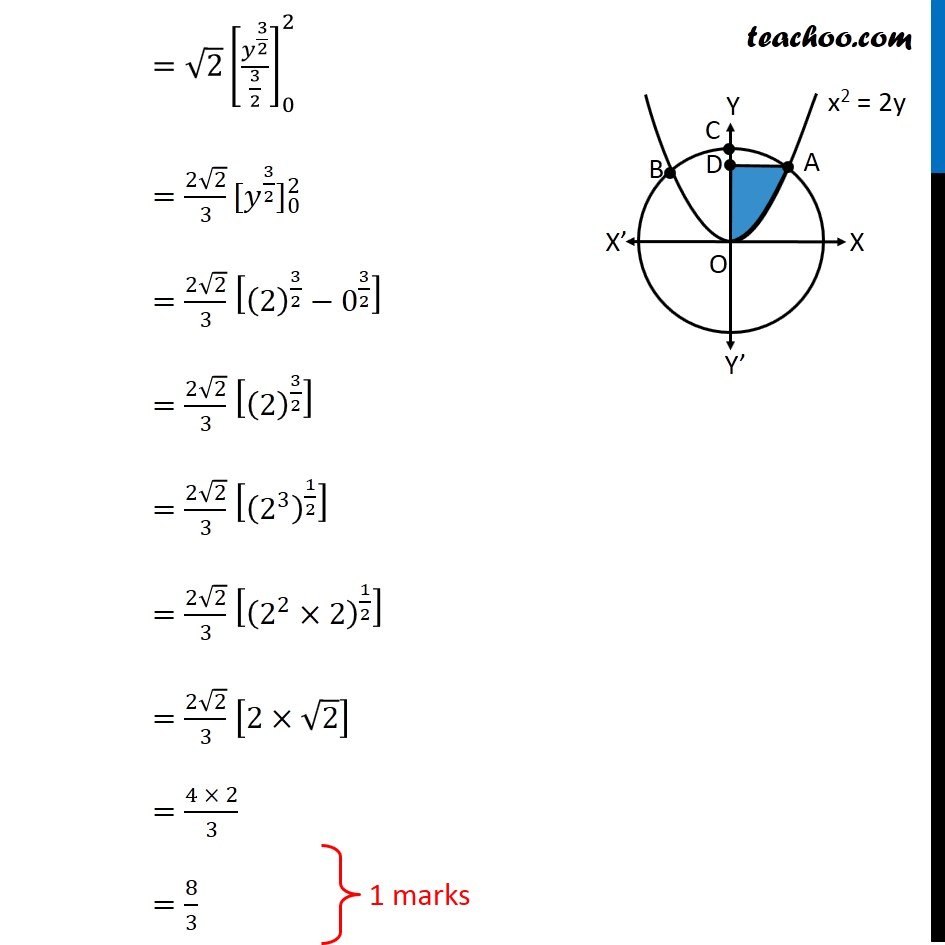
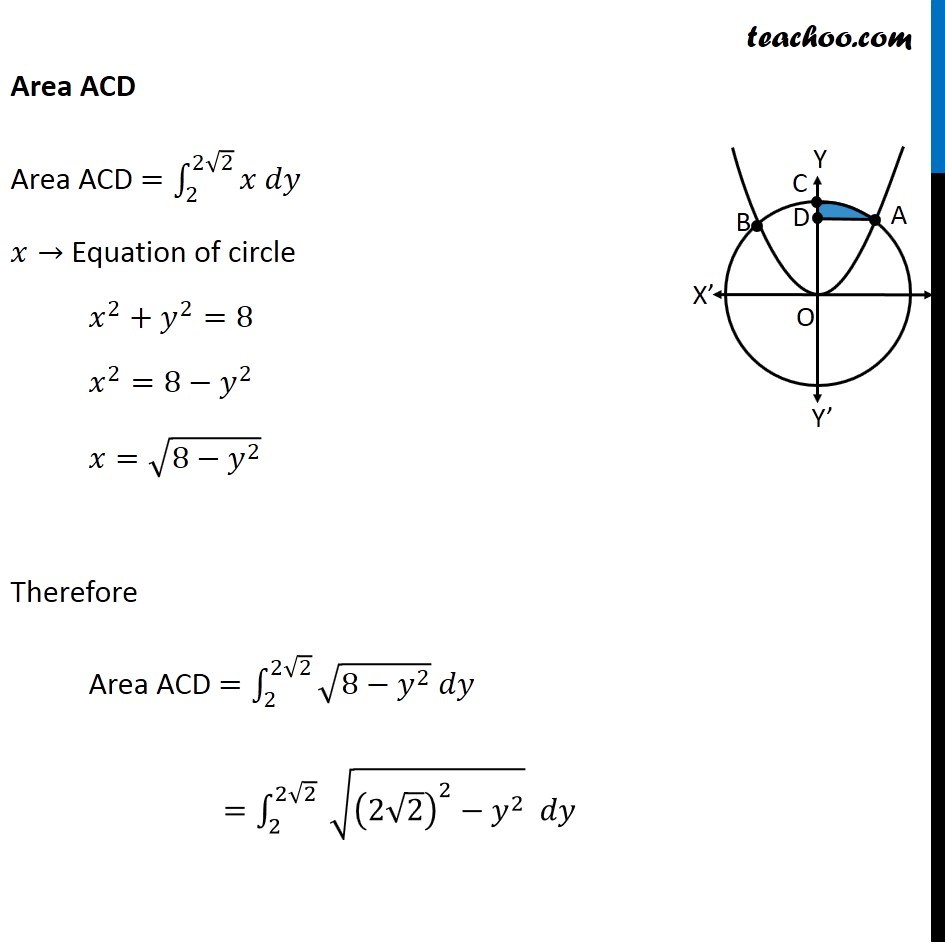
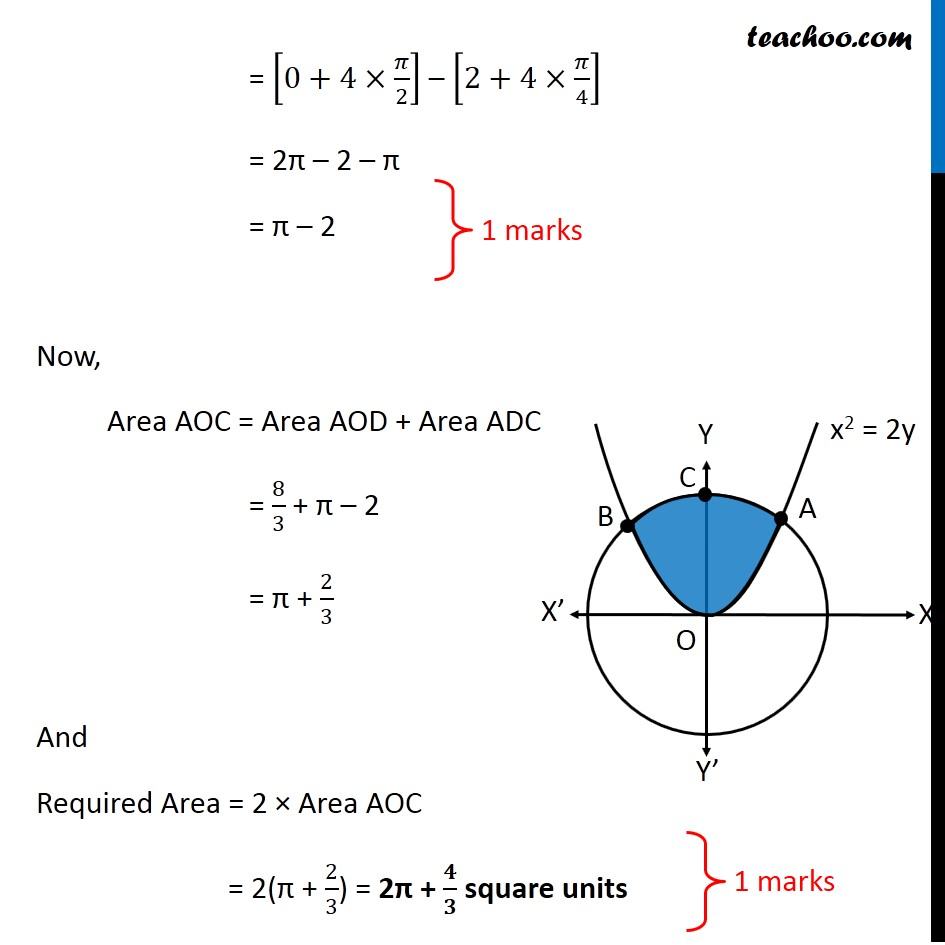
Question 26 (OR 2nd question) Find the area of the region. {(x, y) : x2 + y2 ≤ 8, x2 ≤ 2y} "x2 + y2 ≤ 8" Let’s draw "x2 + y2 = 8" Taking Point (0, 0) "02 + 02 ≤ 8" 0 ≤ 8 Is True So, We Shade inside of graph x2 ≤ 2y Let’s draw x2 = 2y Taking Point (0, 1) 02 ≤ 2 × 1 0 ≤ 2 Is True So, We Shade center of graph Now, our equations are x2 + y2 ≤ 8 x2 ≤ 2y Drawing circle x2 + y2 ≤ 8 x2 + y2 ≤ 4 × 2 𝑥2+ 𝑦2 ≤(2√2)^2 ∴ Radius of circle = 2√2 So, Point C (2√2, 0) Finding point of intersection A & B Finding point of intersection of circle and parallelogram Equation of circle is x2 + y2 = 8 Putting x2 = 2y from parabola 2y + y2 = 8 y2 + 2y – 8 = 0 y2 + 4y – 2y – 8 = 0 y(y + 4) – 2(y + 4) = 0 (y – 2) (y + 4) = 0 So, y = 2, –4 Since point is in positive y-axis y = 2 Putting y = 2 in equation of parabola x2 = 2y x2 = 2(2) x2 = 4 x = ± 2 So, A = (2, 2) and B = (–2, 2) Now, Since figure is symmetric Area AOC = Area BOC ∴ Required Area = Area AOBC = 2 × Area AOC Area AOC Here, point D is (0, 2) Area AOC = Area AOD + Area ADC Let’s find Area AOD and Area ADC separately Area AOD Area AOD =∫_(1/2)^(3/2)▒〖𝑥 𝑑𝑦〗 𝑥→ Equation of parabola 𝑥^2=2𝑦 𝑥=√(2𝑦" " ) Therefore Area AOD =∫_0^2▒〖 √2𝑦 𝑑𝑦〗 =√2 ∫_0^2▒〖 √(𝑦" " ) 𝑑𝑦〗 =√2 ∫_0^2▒〖 𝑦^(1/2) 𝑑𝑥〗 =√2 [𝑦^(3/2)/(3/2)]_0^2 =(2√2)/3 〖[𝑦^(3/2)]〗_0^2 =(2√2)/3 [(2)^(3/2)−0^(3/2) ] =(2√2)/3 [(2)^(3/2) ] =(2√2)/3 [(2^3 )^(1/2) ] =(2√2)/3 [(2^2×2)^(1/2) ] =(2√2)/3 [2×√2] =(4 × 2)/3 =8/3 Area ACD Area ACD =∫_2^(2√2)▒〖𝑥 𝑑𝑦〗 𝑥→ Equation of circle 𝑥^2+𝑦^2=8 𝑥^2=8−𝑦^2 𝑥=√(8−𝑦^2 ) Therefore Area ACD =∫_2^(2√2)▒〖√(8−𝑦^2 ) 𝑑𝑦〗 =∫_2^(2√2)▒〖 √((2√2)^2−𝑦^2 ) 𝑑𝑦〗 It is of form ∫1▒〖√(𝑎^2−𝑥^2 ) 𝑑𝑥=1/2 𝑥√(𝑎^2−𝑥^2 )〗+𝑎^2/2 〖𝑠𝑖𝑛〗^(−1)⁡〖𝑥/𝑎+𝑐〗 Replacing a by 2√2, x with y, we get = [𝑦/2 √((2√2)^2−𝑦^2 )+(2√2)^2/2 sin^(−1)⁡〖𝑦/(2√2)〗 ]_2^(2√2) = [𝑦/2 √(8−𝑦^2 )+8/2 sin^(−1)⁡〖𝑦/(2√2)〗 ]_2^(2√2) = [𝑦/2 √(8−𝑦^2 )+4 sin^(−1)⁡〖𝑦/(2√2)〗 ]_2^(2√2) = [(2√2)/2 √(8−〖(2√2)〗^2 )+4 sin^(−1)⁡〖(2√2)/(2√2)〗 ] – [2/2 √(8−2^2 )+4 sin^(−1)⁡〖2/(2√2)〗 ] = [√2 √(8−8)+4 sin^(−1)⁡1 ] – [√(8−4)+4 sin^(−1)⁡〖1/√2〗 ] = [0+4×𝜋/2] – [2+4×𝜋/4] = 2π – 2 – π = π – 2 Now, Area AOC = Area AOD + Area ADC = 8/3 + π – 2 = π + 2/3 And Required Area = 2 × Area AOC = 2(π + 2/3) = 2π + 𝟒/𝟑 square units