Question 17 (OR 1 st question)
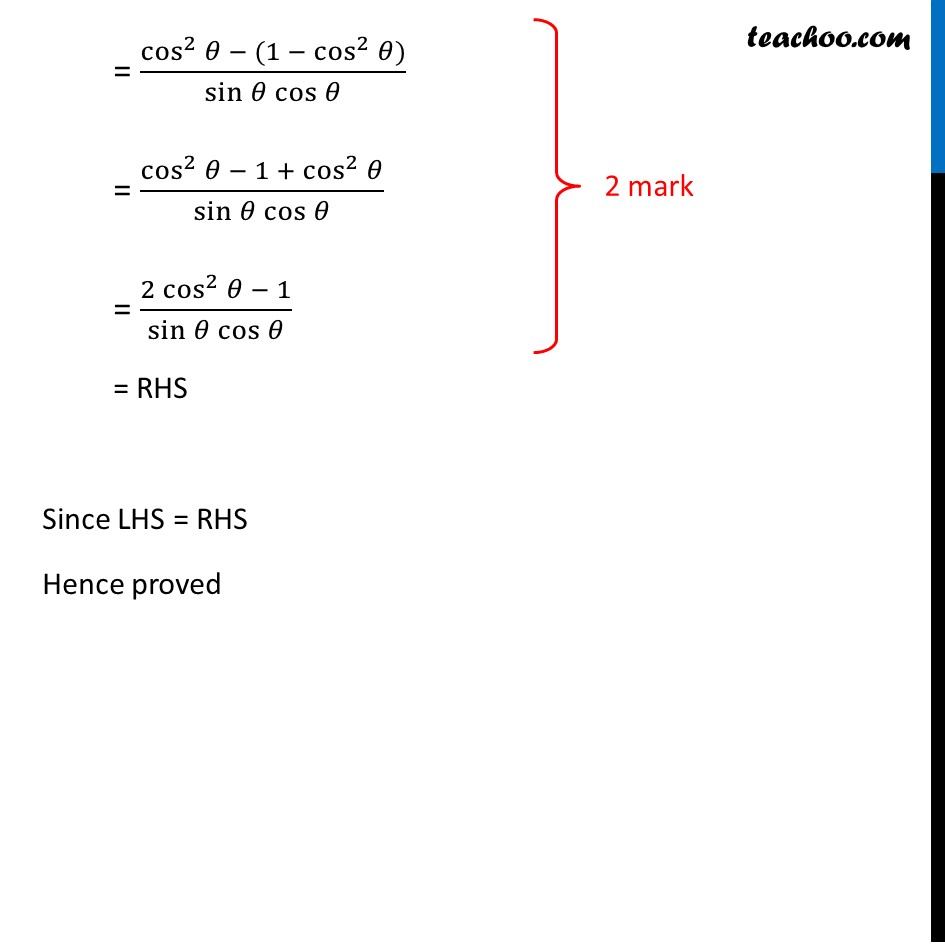
Prove that cot θ - tan θ = (2 cos 2 θ - 1) / (sin θ cos θ)

CBSE Class 10 Sample Paper for 2019 Boards
CBSE Class 10 Sample Paper for 2019 Boards
Last updated at Dec. 16, 2024 by Teachoo
Question 17 (OR 1 st question)
Prove that cot θ - tan θ = (2 cos 2 θ - 1) / (sin θ cos θ)


Transcript
Question 17 (OR 1st question) Prove that cot𝜃−tan𝜃 = (2 cos^2𝜃 − 1)/(sin𝜃 cos𝜃 ) Solving LHS cot𝜃−tan𝜃 = cos𝜃/sin𝜃 −sin𝜃/cos𝜃 = (cos𝜃 × cos𝜃 − sin𝜃 × sin𝜃)/(sin𝜃 cos𝜃 ) = (cos^2𝜃 − sin^2𝜃)/(sin𝜃 cos𝜃 ) Now, sin2 θ + cos2 θ = 1 sin2 θ = 1 – cos2 θ = (cos^2𝜃 − (1 − cos^2𝜃))/(sin𝜃 cos𝜃 ) = (cos^2𝜃 − 1 + cos^2𝜃)/(sin𝜃 cos𝜃 ) = (2 cos^2𝜃 − 1)/(sin𝜃 cos𝜃 ) = RHS Since LHS = RHS Hence proved