Question 4 - Bisector of an angle - Practical Geometry

Transcript

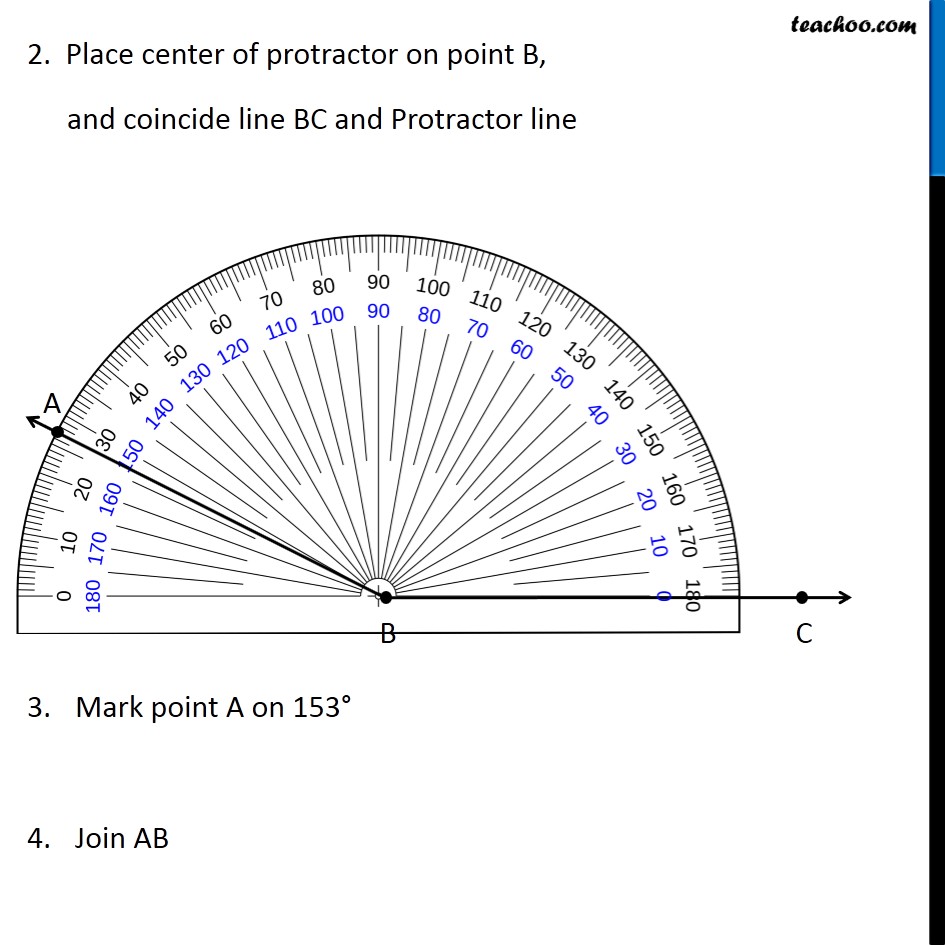
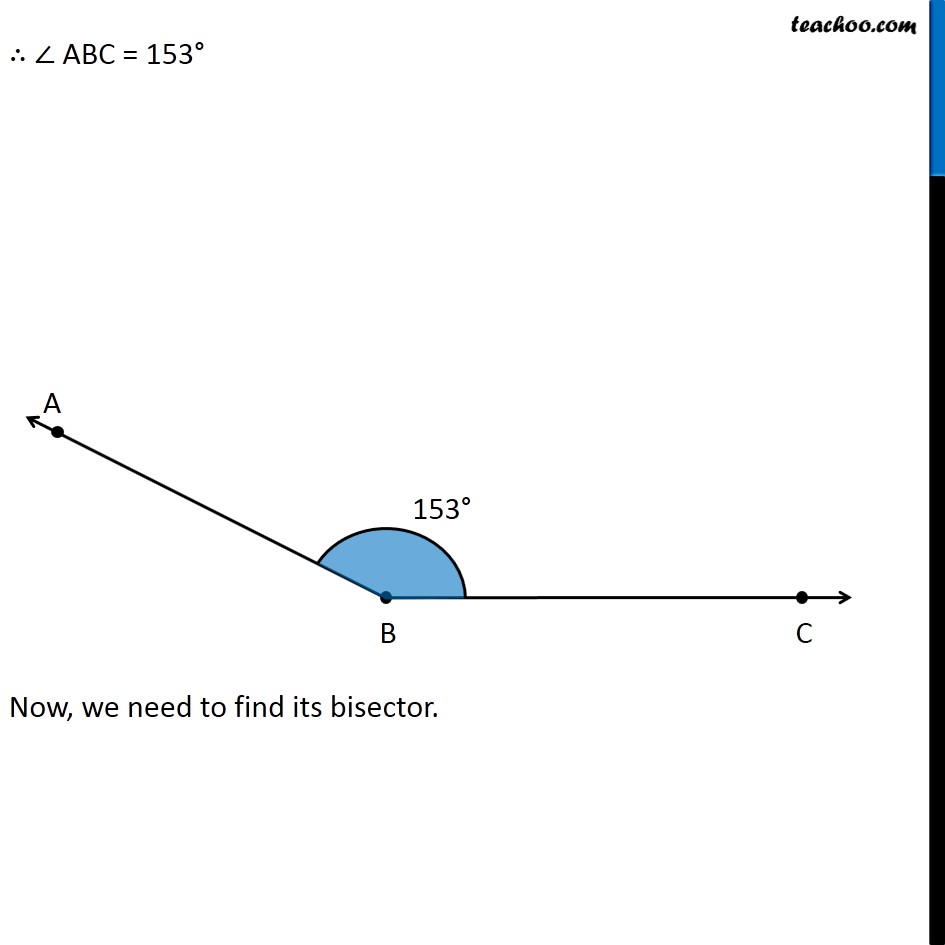
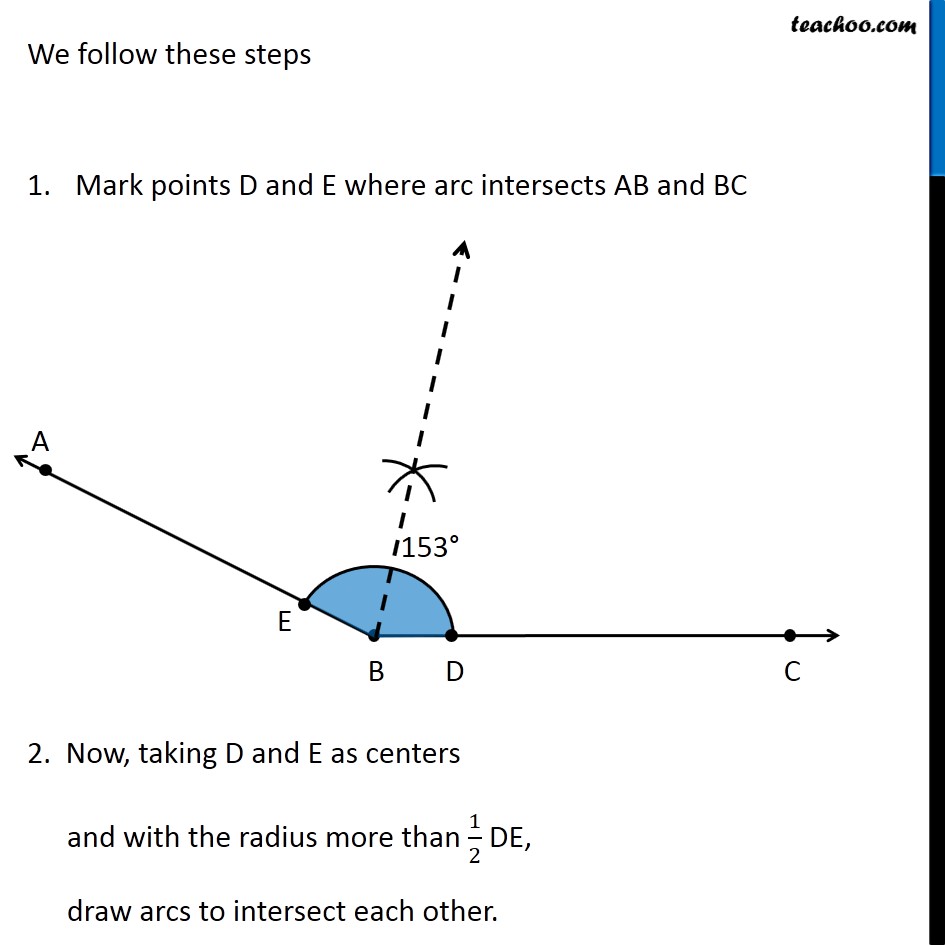
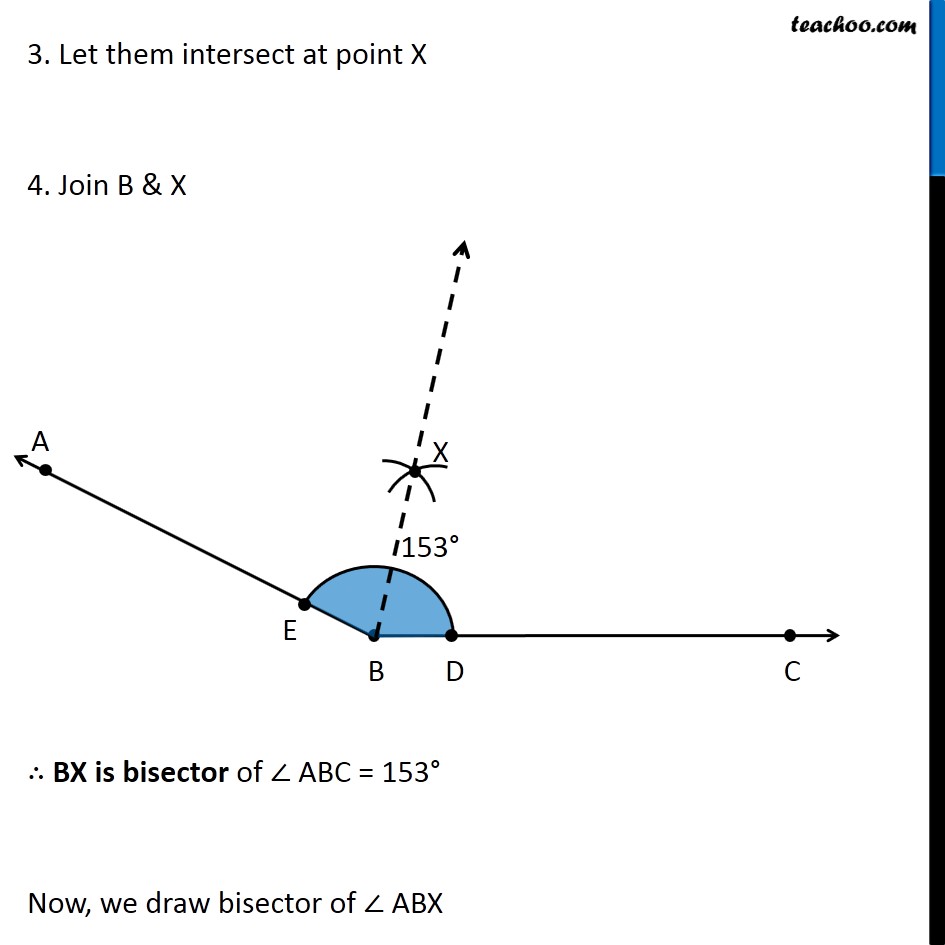
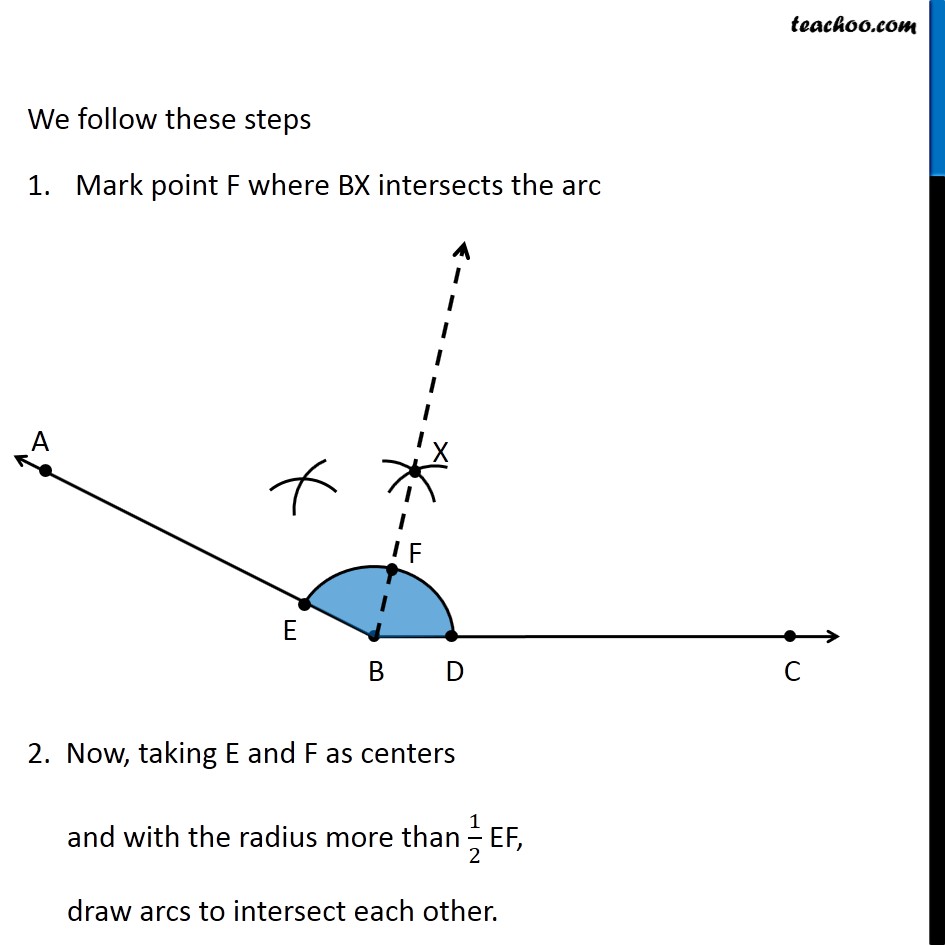
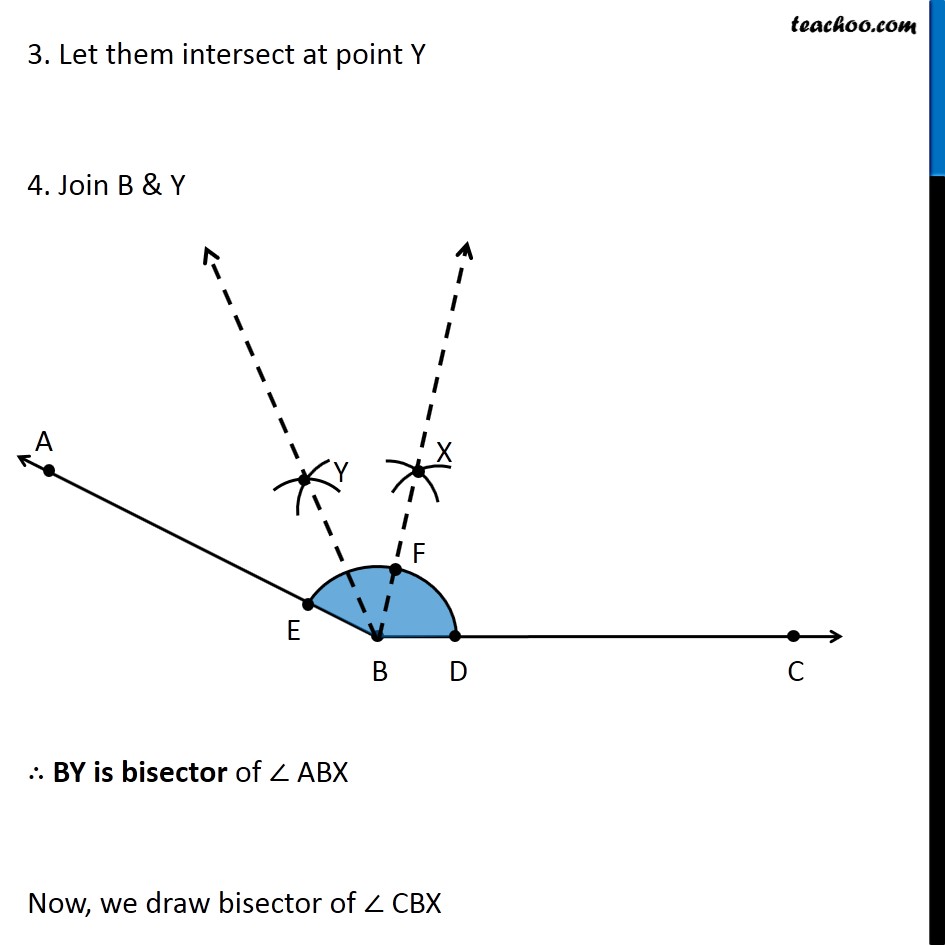
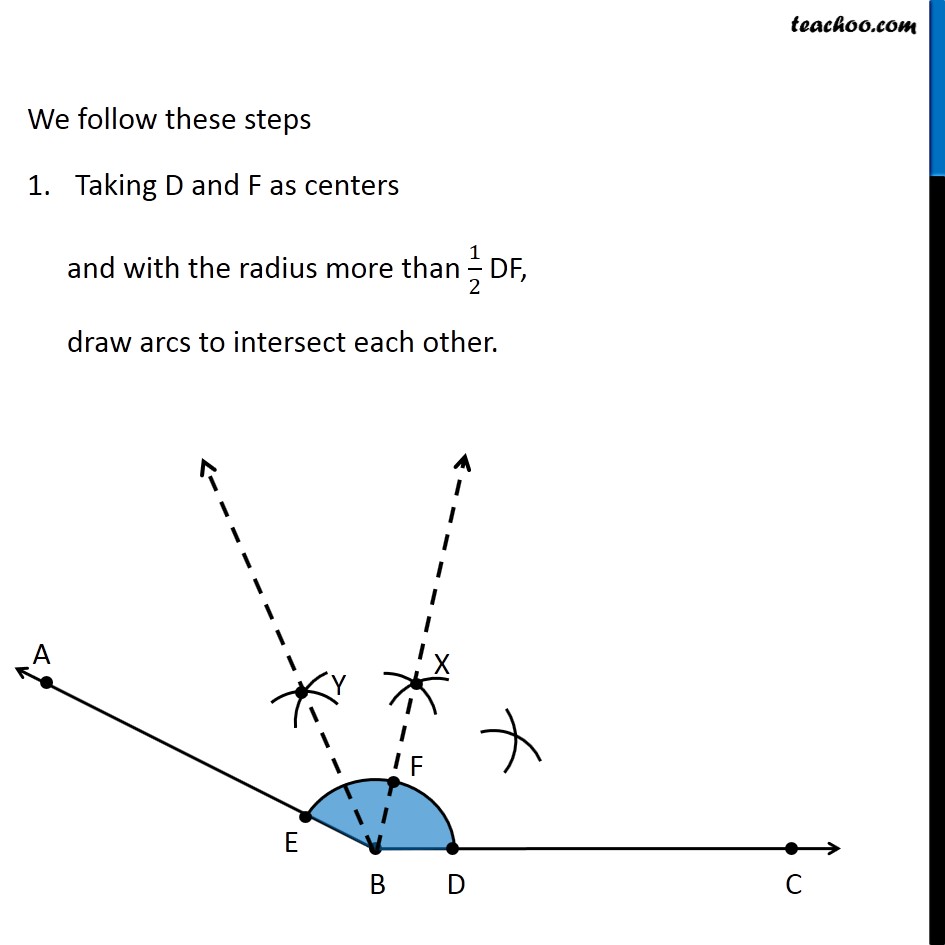
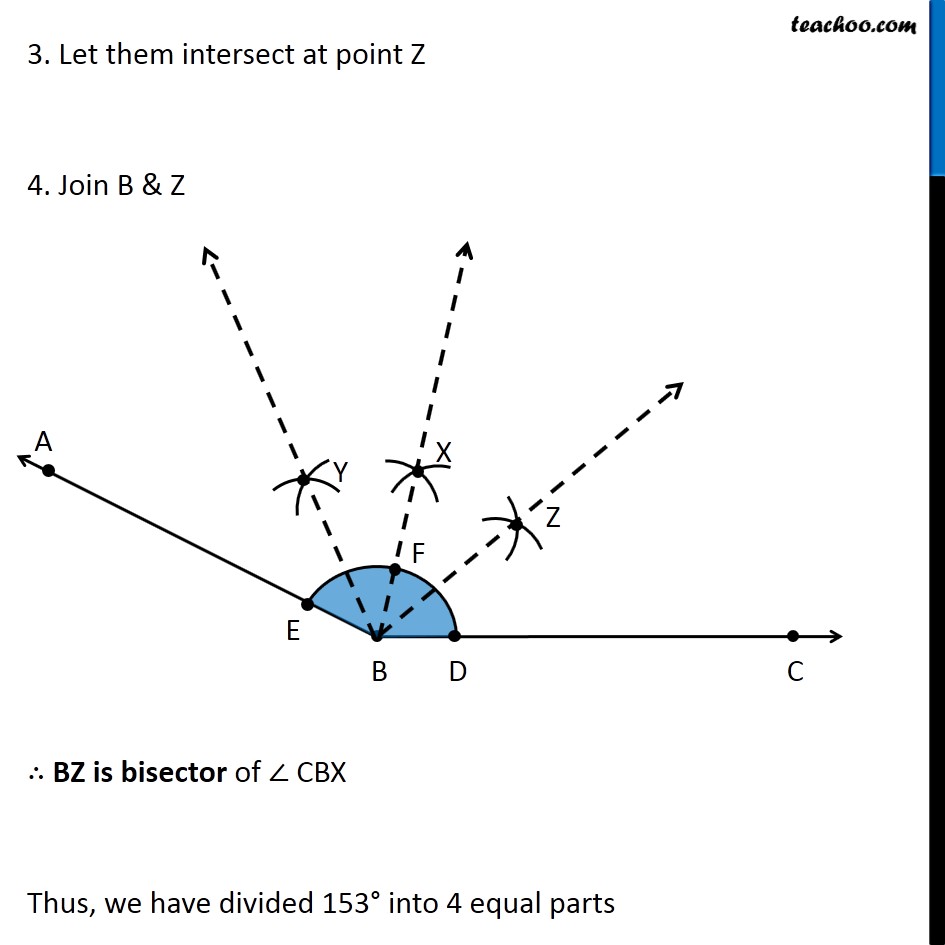
Question 4 Draw an angle of measure 153° and divide it into four equal parts Let’s draw a rough diagram Suppose ∠ ABC = 153° So, first we bisector of ∠ ABC, then bisector of ∠ ABX & then bisector of ∠ CBX Then, ∠ ABC will be divided into 4 equal parts Let’s follow these steps Draw a ray BC 2. Place center of protractor on point B, and coincide line BC and Protractor line Mark point A on 153° Join AB ∴ ∠ ABC = 153° Now, we need to find its bisector. We follow these steps 1. Mark points D and E where arc intersects AB and BC 2. Now, taking D and E as centers and with the radius more than 1/2 DE, draw arcs to intersect each other. 3. Let them intersect at point X 4. Join B & X ∴ BX is bisector of ∠ ABC = 153° Now, we draw bisector of ∠ ABX We follow these steps Mark point F where BX intersects the arc 2. Now, taking E and F as centers and with the radius more than 1/2 EF, draw arcs to intersect each other 3. Let them intersect at point Y 4. Join B & Y ∴ BY is bisector of ∠ ABX Now, we draw bisector of ∠ CBX We follow these steps Taking D and F as centers and with the radius more than 1/2 DF, draw arcs to intersect each other. 3. Let them intersect at point Z 4. Join B & Z ∴ BZ is bisector of ∠ CBX Thus, we have divided 153° into 4 equal parts