Question 8 - Perpendicular bisector of a line segment - Practical Geometry

Transcript

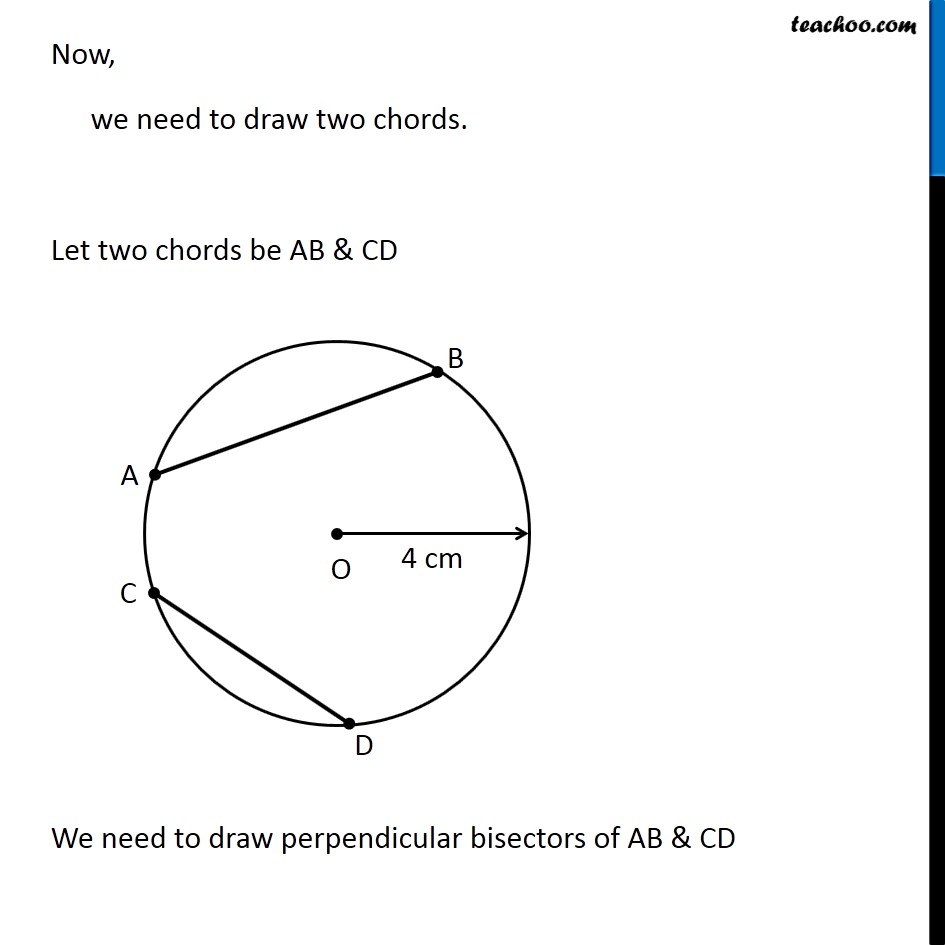
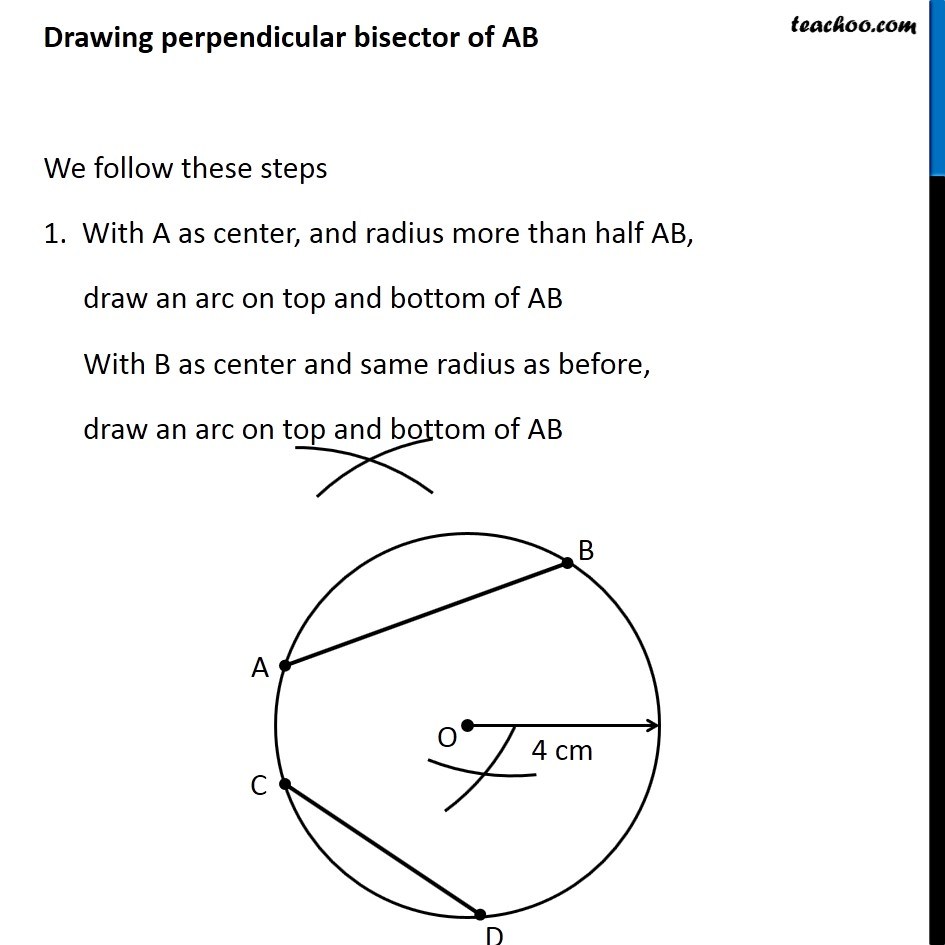
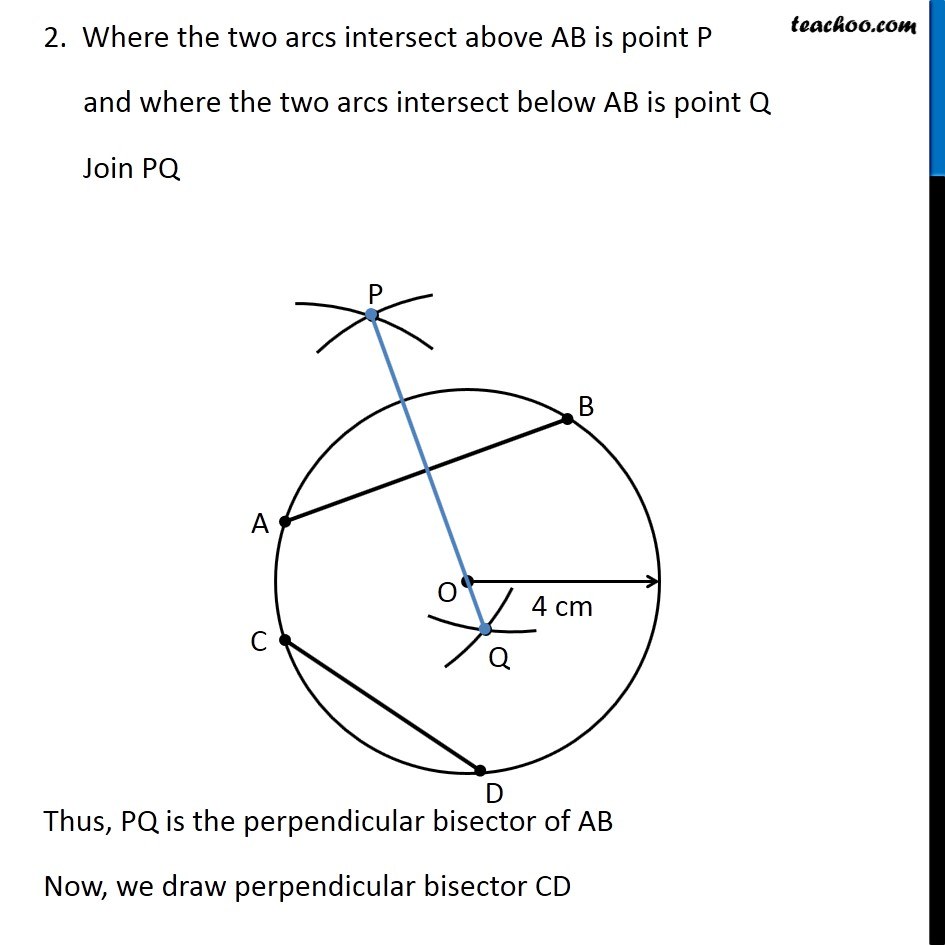
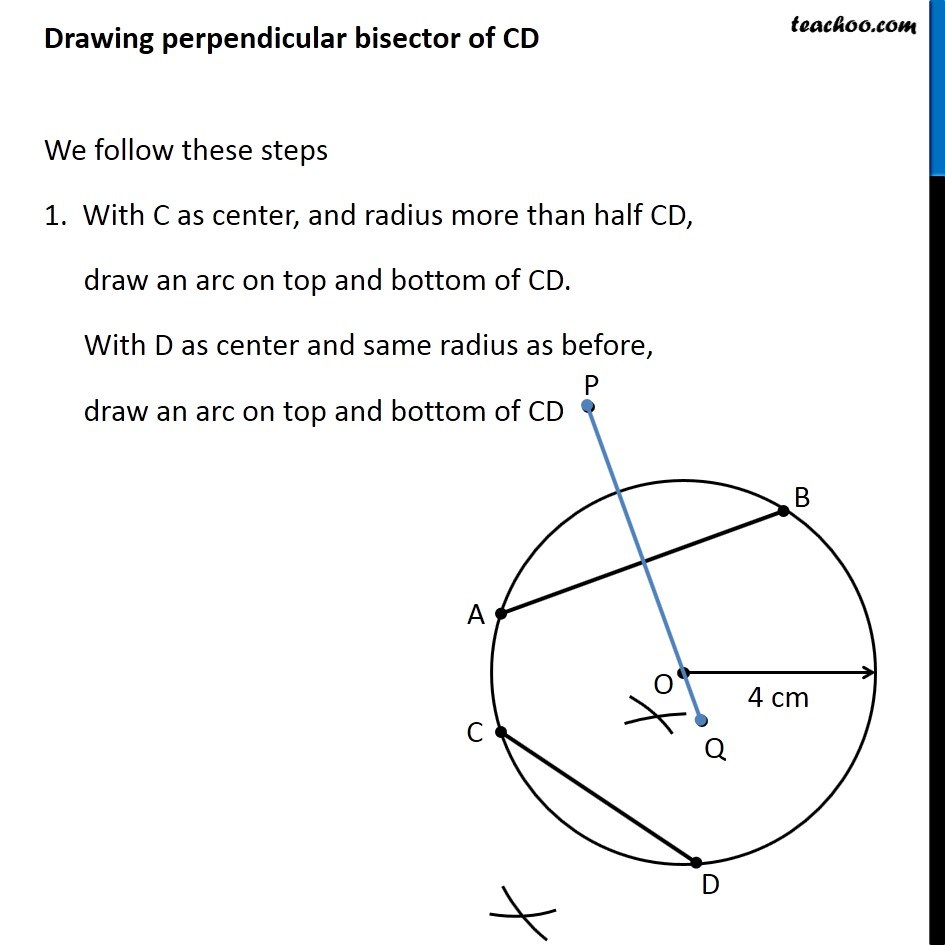
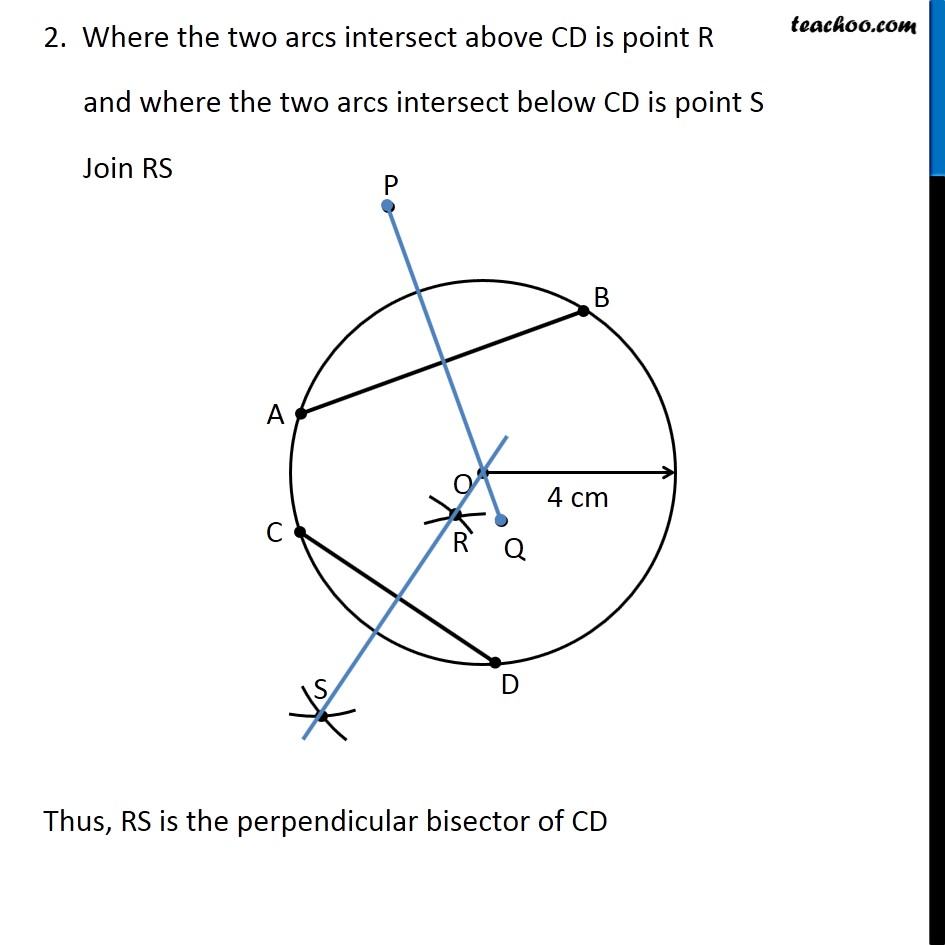
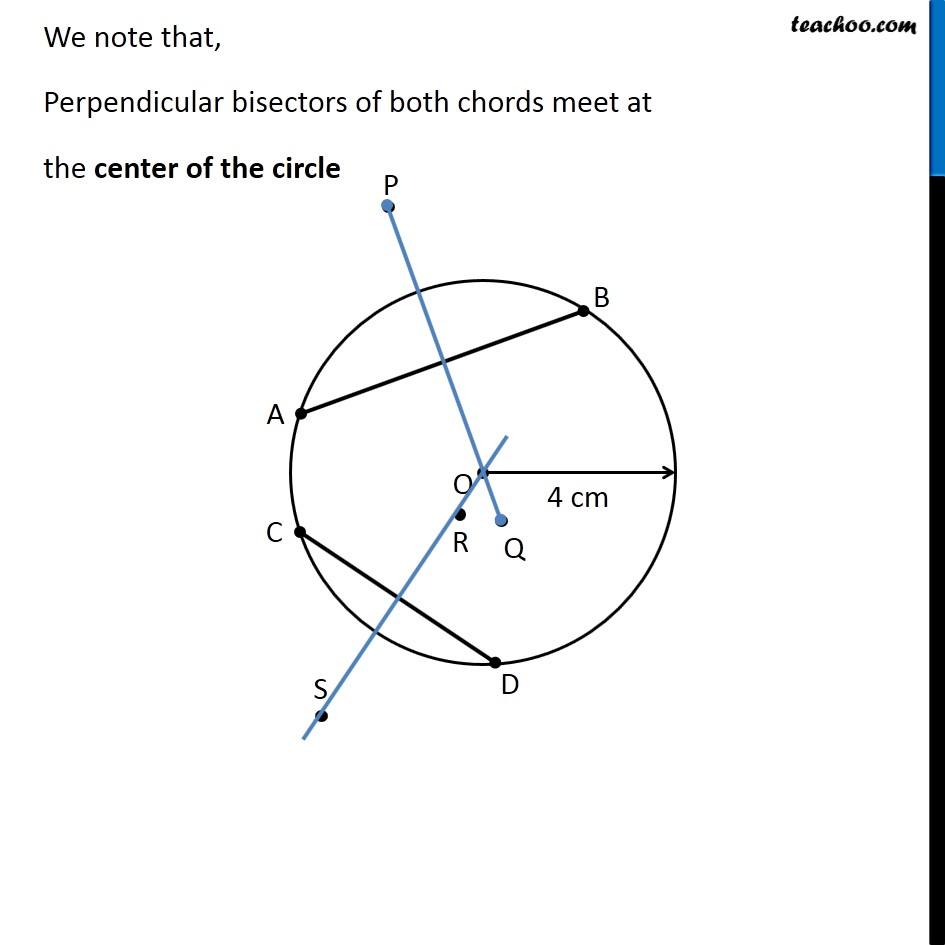
Question 8 Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet? Let’s first draw a circle of radius 3.4 cm We follow these steps 1. Mark point O as center 2. First we make circle of radius 4 cm Since radius is 4 cm, we measure 4 cm using ruler and compass 3. Now keeping compass opened the same length. We keep pointed end at the center, and draw a circle using the pencil end of the compass So, this is the required circle with center O and radius = 4 cm Now, we need to draw two chords. Let two chords be AB & CD We need to draw perpendicular bisectors of AB & CD Drawing perpendicular bisector of AB We follow these steps 1. With A as center, and radius more than half AB, draw an arc on top and bottom of AB With B as center and same radius as before, draw an arc on top and bottom of AB 2. Where the two arcs intersect above AB is point P and where the two arcs intersect below AB is point Q Join PQ Thus, PQ is the perpendicular bisector of AB Now, we draw perpendicular bisector CD Drawing perpendicular bisector of CD We follow these steps 1. With C as center, and radius more than half CD, draw an arc on top and bottom of CD. With D as center and same radius as before, draw an arc on top and bottom of CD 2. Where the two arcs intersect above CD is point R and where the two arcs intersect below CD is point S Join RS Thus, RS is the perpendicular bisector of CD We note that, Perpendicular bisectors of both chords meet at the center of the circle