Question 4 - Perpendicular bisector of a line segment - Practical Geometry

Transcript

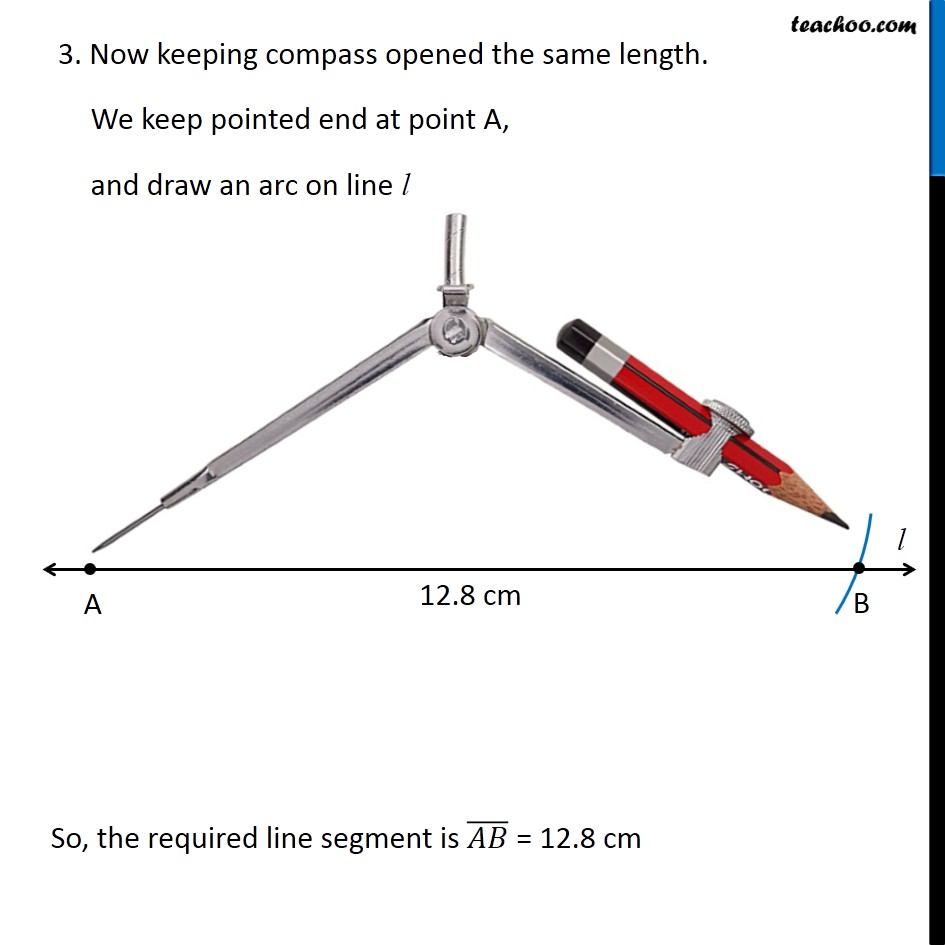
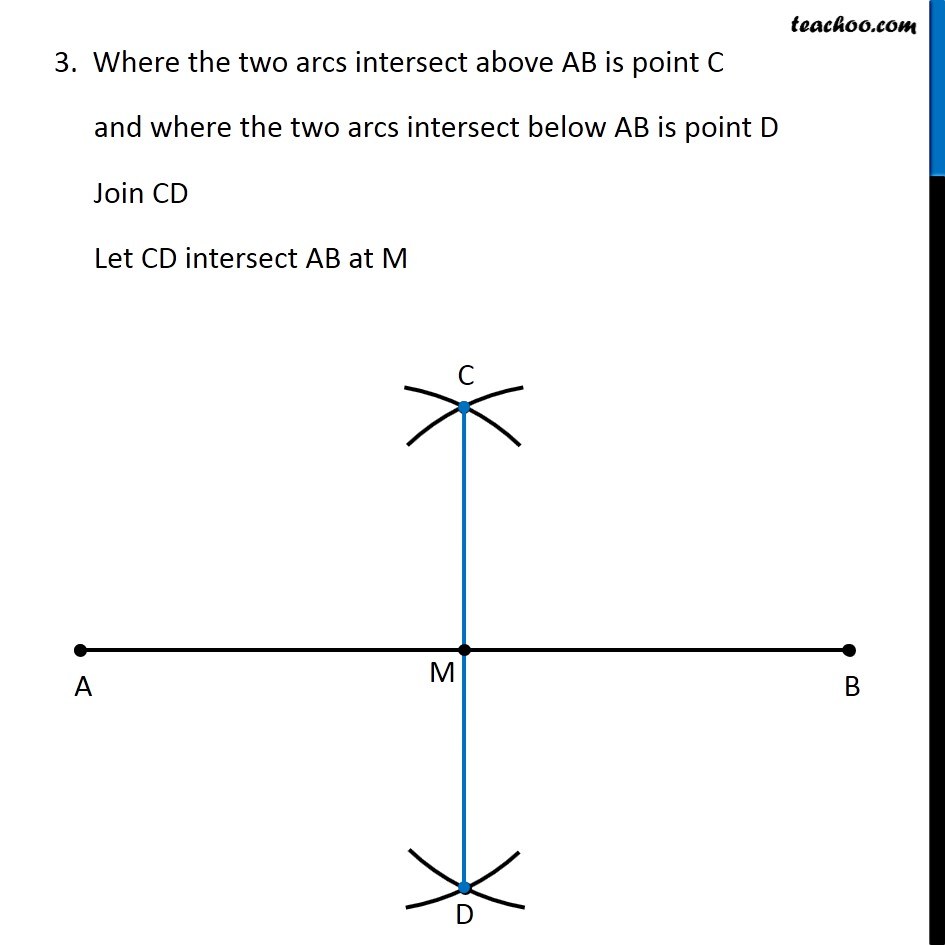
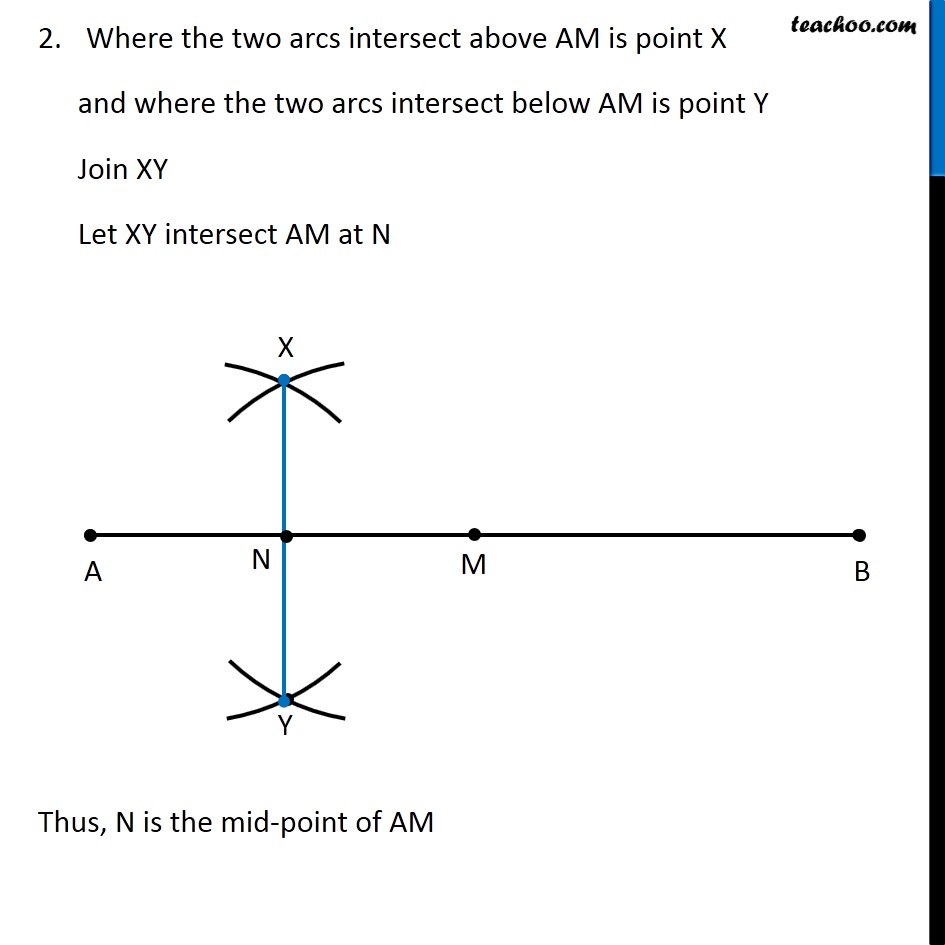
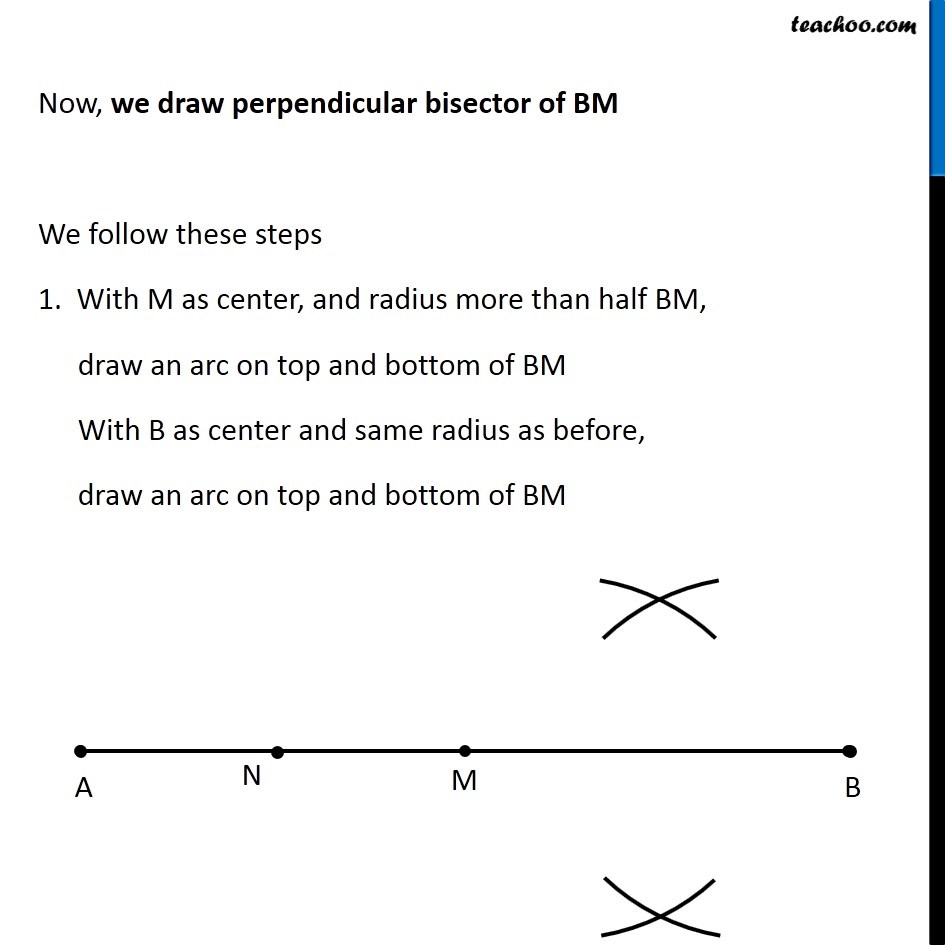
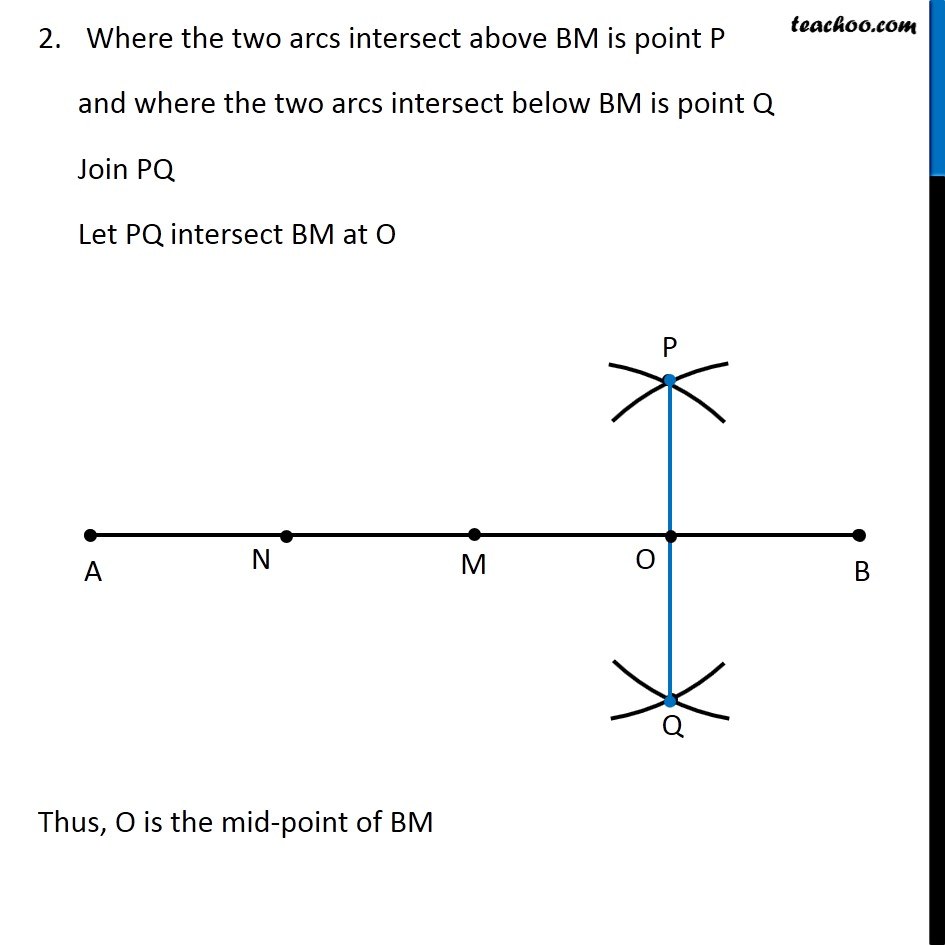
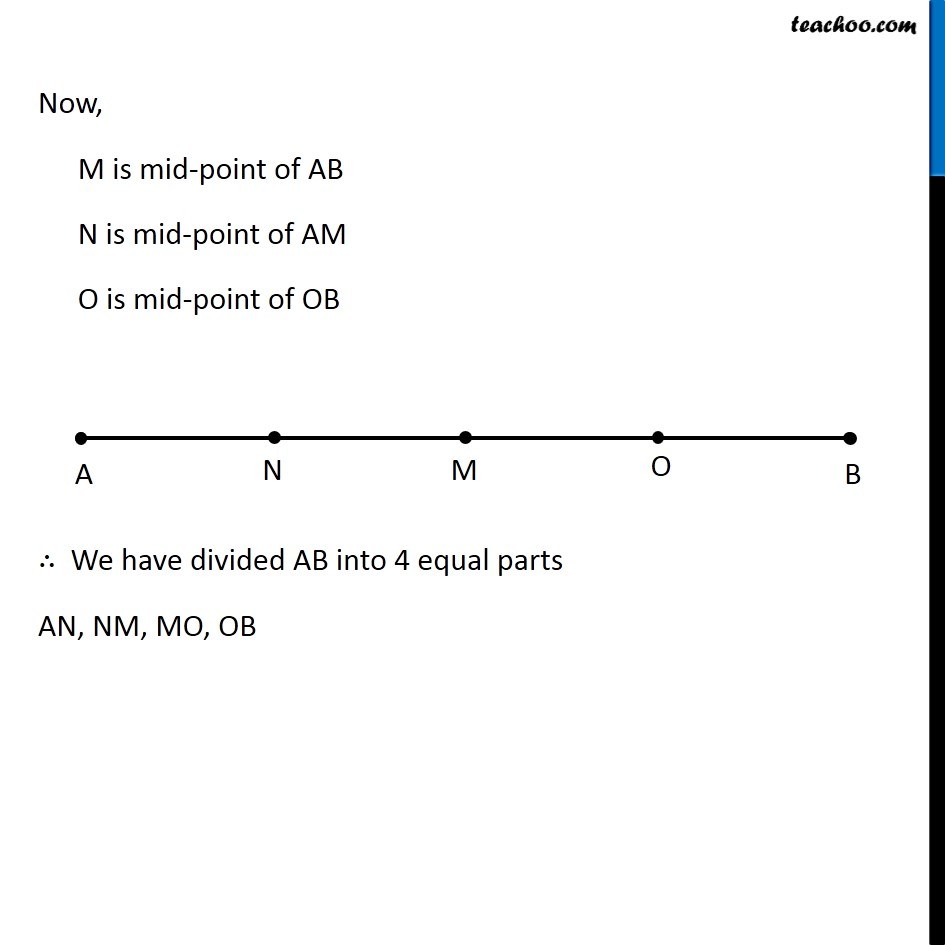
Question 4 Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement. Here, We need to divide a line segment into 4 equal parts So, let’s draw a rough diagram Thus, We make perpendicular bisector of AB, then perpendicular bisector of AM, and then perpendicular bisector of BM Let’s first draw a line segment of 12.8 cm and then draw its perpendicular We follow these steps 1. Draw a line l mark point A on it 2. Since length is 12.8 cm, we measure 12.8 cm using ruler and compass 3. Now keeping compass opened the same length. We keep pointed end at point A, and draw an arc on line l So, the required line segment is (𝐴𝐵) ̅ = 12.8 cm Now, we need to find its perpendicular bisector Let’s follow these steps to make perpendicular bisector of AB 1. Given a line segment AB. Now with A as center, and radius more than half AB, draw an arc on top and bottom of AB With B as center and same radius as before, draw an arc on top and bottom of AB 3. Where the two arcs intersect above AB is point C and where the two arcs intersect below AB is point D Join CD Let CD intersect AB at M Thus, M is the mid-point of AB Now, we draw perpendicular bisector of AM We follow these steps 1. With A as center, and radius more than half AM, draw an arc on top and bottom of AM With M as center and same radius as before, draw an arc on top and bottom of AM Where the two arcs intersect above AM is point X and where the two arcs intersect below AM is point Y Join XY Let XY intersect AM at N Thus, N is the mid-point of AM Now, we draw perpendicular bisector of BM We follow these steps 1. With M as center, and radius more than half BM, draw an arc on top and bottom of BM With B as center and same radius as before, draw an arc on top and bottom of BM Where the two arcs intersect above BM is point P and where the two arcs intersect below BM is point Q Join PQ Let PQ intersect BM at O Thus, O is the mid-point of BM Now, M is mid-point of AB N is mid-point of AM O is mid-point of OB ∴ We have divided AB into 4 equal parts AN, NM, MO, OB