Linear pair is a pair of adjacent angles where non-common side forms a straight line
So, In a linear pair, there are two angles who have
- Common vertex
- Common side
- Non-common side makes a straight line or Sum of angles is 180°

Linear pair
Linear pair is a pair of adjacent angles where non-common side forms a straight line
So, In a linear pair, there are two angles who have
- Common vertex
- Common side
- Non-common side makes a straight line or Sum of angles is 180°

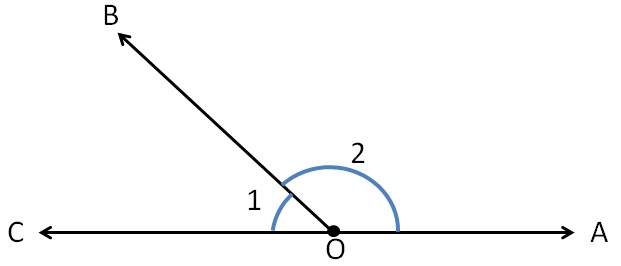
Here, these angles are in linear pair as
- They have common vertex O.
- They have common side OB
-
Non Common side (AC) is a straight line.
Here,
∠1 + ∠2 = 180°
Sum of linear pair = 180°
Let’s take this figure

In this figure
∠1 & ∠2 are linear pair
∠2 & ∠3 are linear pair
∠3 & ∠4 are linear pair
∠4 & ∠1 are linear pair

So,
∠1 + ∠2 = 180°
∠2 + ∠3 = 180°
∠3 + ∠4 = 180°
∠4 + ∠1 = 180°
Let’s take some more examples.
Do the angles form a linear pair?

Here,
Angles have a common vertex O,
They have a common side OB
Now,
Sum of angles = 40° + 140°
= 180°
∴ Non-common sides from a line
Hence, angles form a linear pair.
Do the angles form a linear pair?

Here,
Angles have a common vertex O,
They have a common side OB
But,
Non-common side of ∠1 and ∠2
Do not form a line
∴ They do not form a linear pair
Do the angles form a linear pair?

Here,
Angles have a common vertex O,
They have a common side OQ
Now,
Sum of angles = 60° + 90°
= 150°
≠ 180°
∴ Non-common sides do not form a line
Hence, angle do not form a linear pair
Do the angles form a linear pair?

Here,
Angle do not have common vertex
∴ They do not form a linear pair
Do the angles form a linear pair?

Here,
Angles have a common vertex O,
They have a common base OB
Now,
Sum of angles = 65° + 115° = 180°
Since sum of angles is 180°
∴ They form a linear pair
