Question 1 - Finding cube root by estimation - Chapter 6 Class 8 Cubes and Cube Roots

Last updated at Dec. 16, 2024 by

Ex 7.2, 3 - You are told that 1,331 is a perfect cube. Can you guess

Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 2
Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 3
Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 4
Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 5 Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 6 Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 7 Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 8 Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 9 Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 10 Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 11 Ex 7.2, 3 - Chapter 7 Class 8 Cubes and Cube Roots - Part 12

Go Ad-free

Transcript

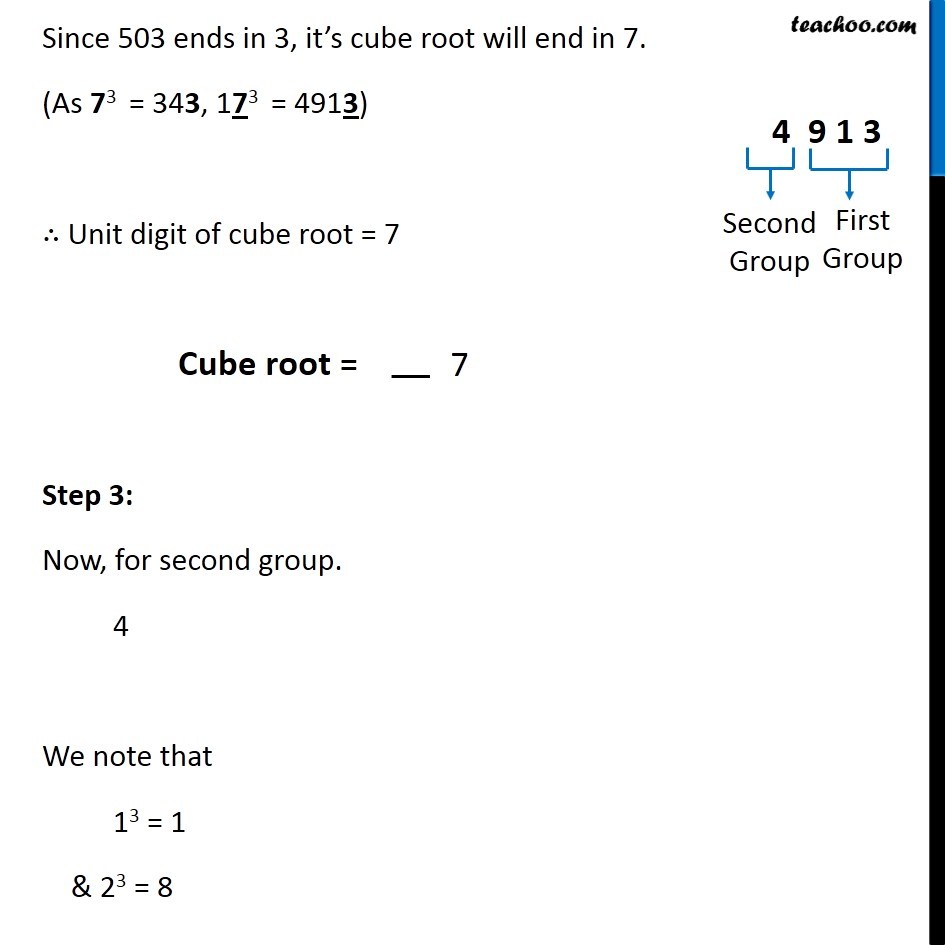
Question 1 You are told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768. Step 1: Make group of 3 digit, starting from right Step 2: The unit digit of cube root will be Unit digit of cube root of 1331 = Unit digit of cube root of 331 Since 331 ends in 1, it’s cube root will end in 1. (As 13 = 1, 113 = 1331) ∴ Unit digit of cube root = 1 Step 3: Now, for second group. 1 We note that 13 = 1 So, We put 1 in ten’s place of cube root. ∴ Cube root of 1331 = 11 Find cube root of 4913. Step 1: Make group of 3 digit, starting from right Step 2: The unit digit of cube root will be Unit digit of cube root of 4913 = Unit digit of cube root of 913 Since 503 ends in 3, it’s cube root will end in 7. (As 73 = 343, 173 = 4913) ∴ Unit digit of cube root = 7 Step 3: Now, for second group. 4 We note that 13 = 1 & 23 = 8 So, 1 < 4 < 8 13 < 4 < 23 ∴ We take smaller number So, 1 We put 1 in ten’s place of cube root. ∴ Cube root of 4913 = 17 Find cube root of 12167. Step 1: Make group of 3 digit, starting from right Step 2: The unit digit of cube root will be Unit digit of cube root of 12167 = Unit digit of cube root of 167 Since 617 ends in 7, it’s cube root will end in 3. (As 33 = 27, 133 = 2797) ∴ Unit digit of cube root = 3 Step 3: Now, for second group. 12 We note that 23 = 8 & 33 =27 So, 8 < 12 < 27 23 < 12 < 33 ∴ We take smaller number So, 2 We put 2 in ten’s place of cube root. ∴ Cube root of 12167 = 23 Find cube root of 32768. Step 1: Make group of 3 digit, starting from right Step 2: The unit digit of cube root will be Unit digit of cube root of 32768 = Unit digit of cube root of 768 Since 768 ends in 8, it’s cube root will end in 3. (As 23 = 8, 123 = 1728) ∴ Unit digit of cube root = 2 Step 3: Now, for second group. 32 We note that 33 = 27 & 43 = 64 So, 27 < 32 < 64 33 < 22 < 43 ∴ We take smaller number So, 3 We put 3 in ten’s place of cube root. ∴ Cube root of 32678 = 32

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo