You are here
Ex 5.4, 7 - Chapter 5 Class 8 Squares and Square Roots
Last updated at April 16, 2024 by Teachoo
Chapter 5 Class 8 Squares and Square Roots
Concept wise
- Square numbers
- Properties of square numbers
- Sum of consecutive odd numbers
- Numbers between square numbers
- Pattern Solving
- Finding square of large numbers
- Pythagorean triplets
- Square root
- Finding Square root through repeated subtraction
- Finding Square root through prime factorisation
- Checking if perfect square by prime factorisation
- Smallest number multiplied to get perfect square
- Smallest number divided to get perfect square
- Smallest square number divisible by numbers
- Finding number of digits in square root (without calculation)
- Finding square root by division method - Integers
- Least number subtracted to get a perfect square
- Least number added to get a perfect square
- Finding square root by division method - Decimals
-
Statement Questions
Transcript
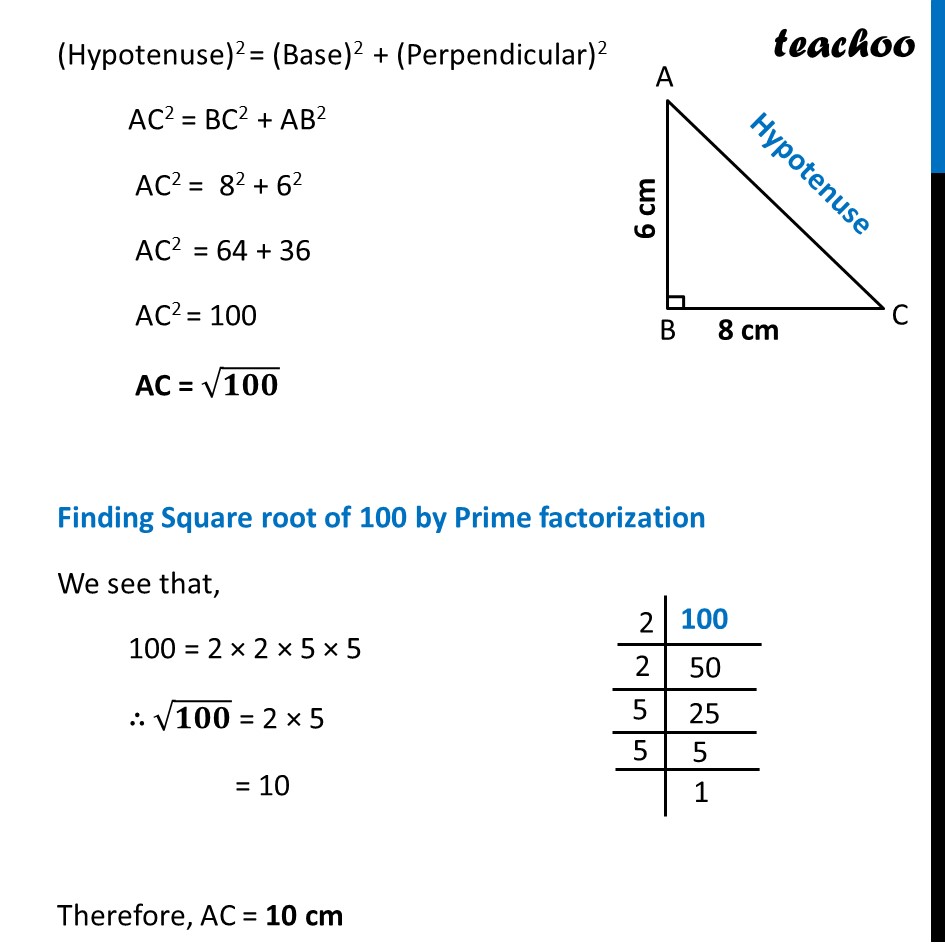
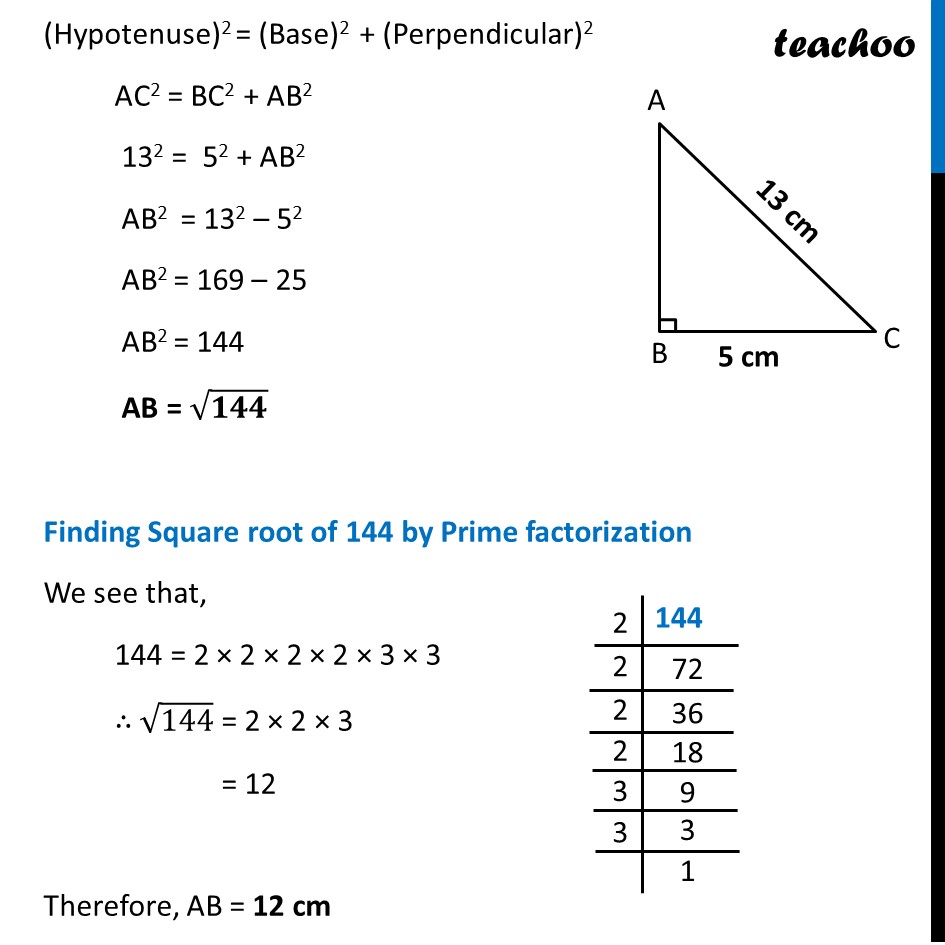
Ex 5.4, 7 In a right triangle ABC, ∠B = 90°. (a) If AB = 6 cm, BC = 8 cm, find AC Given, ∠B = 90° AB = 6 cm BC = 8 cm In right angled triangle ∆ABC, Using Pythagoras theorem, Hypotenuse is the side opposite to right angle. (Hypotenuse)2 = (Base)2 + (Perpendicular)2 AC2 = BC2 + AB2 AC2 = 82 + 62 AC2 = 64 + 36 AC2 = 100 AC = √𝟏𝟎𝟎 Finding Square root of 100 by Prime factorization We see that, 100 = 2 × 2 × 5 × 5 ∴ √𝟏𝟎𝟎 = 2 × 5 = 10 Therefore, AC = 10 cm Ex 5.4, 7 In a right triangle ABC, ∠B = 90°. (b) If AC = 13 cm, BC = 5 cm, find AB Given, ∠B = 90° AC = 13 cm BC = 5 cm In right angled triangle ∆ABC, Using Pythagoras theorem, (Hypotenuse)2 = (Base)2 + (Perpendicular)2 AC2 = BC2 + AB2 132 = 52 + AB2 AB2 = 132 – 52 AB2 = 169 – 25 AB2 = 144 AB = √𝟏𝟒𝟒 Finding Square root of 144 by Prime factorization We see that, 144 = 2 × 2 × 2 × 2 × 3 × 3 ∴ √144 = 2 × 2 × 3 = 12 Therefore, AB = 12 cm
