You are here
Question 3 - Forming Linear Equations - Perimeter and Area - Chapter 2 Class 8 Linear Equations in One Variable
Last updated at Dec. 16, 2024 by Teachoo
Forming Linear Equations - Perimeter and Area
Chapter 2 Class 8 Linear Equations in One Variable
Concept wise
- Definitions
- Solving Linear Equations - Variables on 1 side
- Solving Linear Equations - Variables on both sides
- Solving Linear Equations - Making equation simpler and then solving
-
Forming Linear Equations - Perimeter and Area
- Forming Linear Equations - Fraction - Denominator & Numerator
- Forming Linear Equations - Cost, Sale, Profit
- Forming Linear Equations - Consecutive Numbers
- Forming Linear Equations - Consecutive Multiples
- Forming Linear Equations - Coins and Currency Notes
- Forming Linear Equations - Adding subtracting numbers
- Forming Linear Equations - Two digit number
- Forming Linear Equations - Age
Transcript
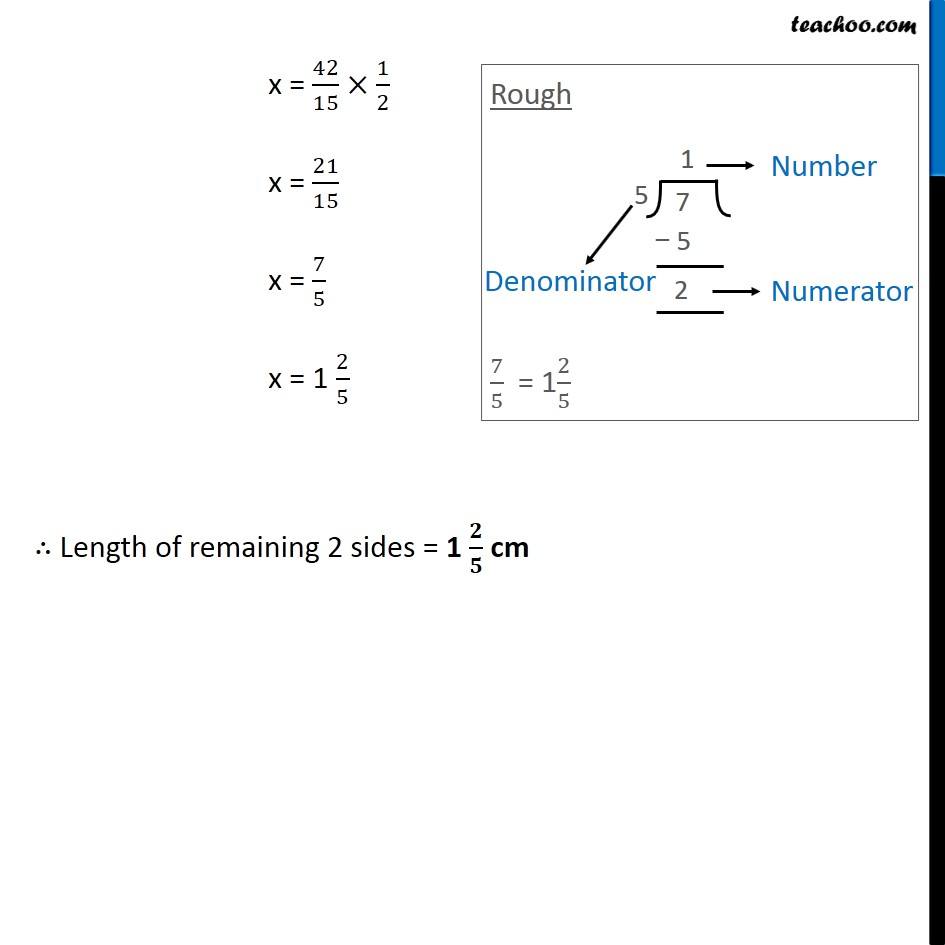
Question 3 The base of an isosceles triangle is 4/3 cm. The perimeter of the triangle is 4 2/15 cm. What is the length of either of the remaining equal sides? Let Δ ABC be an isosceles triangle Base = BC = 4/3 cm Let AB = x So BC = x (Two sides of an isosceles triangle are equal) Given, Perimeter = 4 2/15 cm = (4 × 15 + 2)/15 = (60 + 2)/15 = 62/15 Also, Perimeter = Sum of sides 62/15= AB + AC + BC 62/15= x + x + 4/3 62/15= 2x + 4/3 2x + 4/3 = 62/15 2x = 62/15− 4/3 2x = (62 − 4 × 5 )/15 2x = (62 − 20)/15 2x = 42/15 x = 42/15×1/2 x = 21/15 x = 7/5 x = 1 2/5 ∴ Length of remaining 2 sides = 1 𝟐/𝟓 cm Rough Converting 7/5 into mixed fraction 7/5 = 1 2/5
