Question 7 - Important Questions on Surface Area and Volume - Chapter 12 Class 10 Surface Areas and Volumes

Transcript

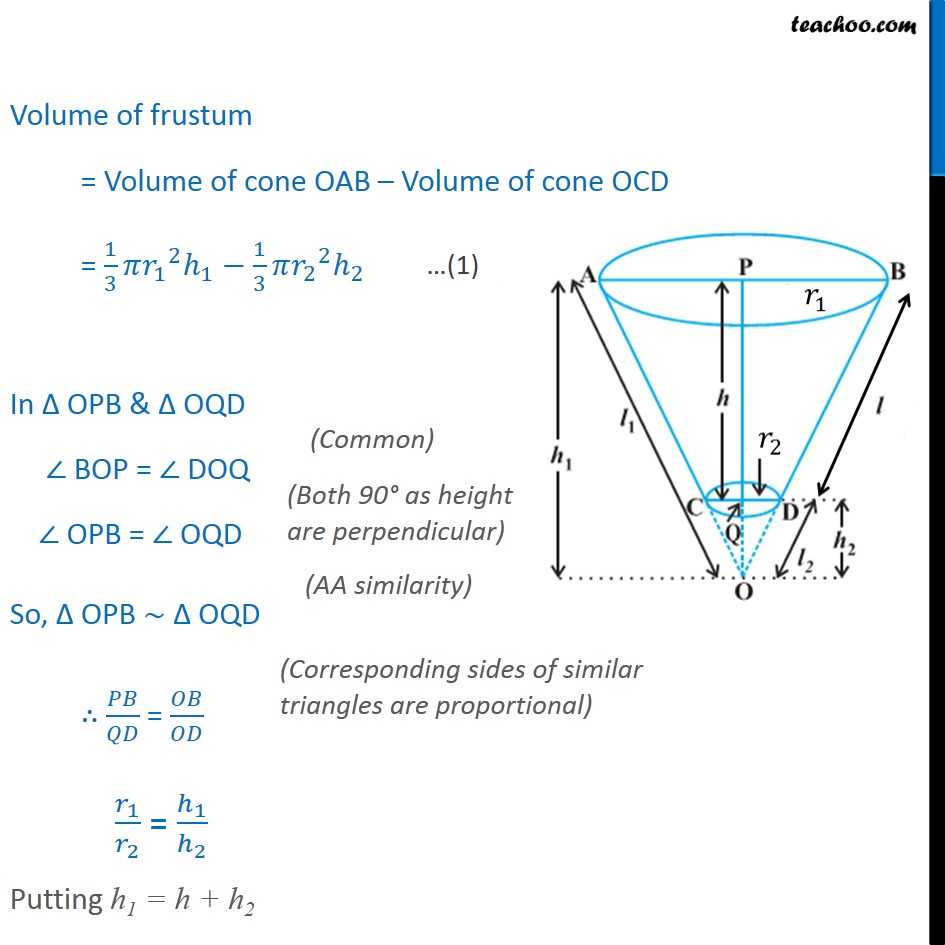
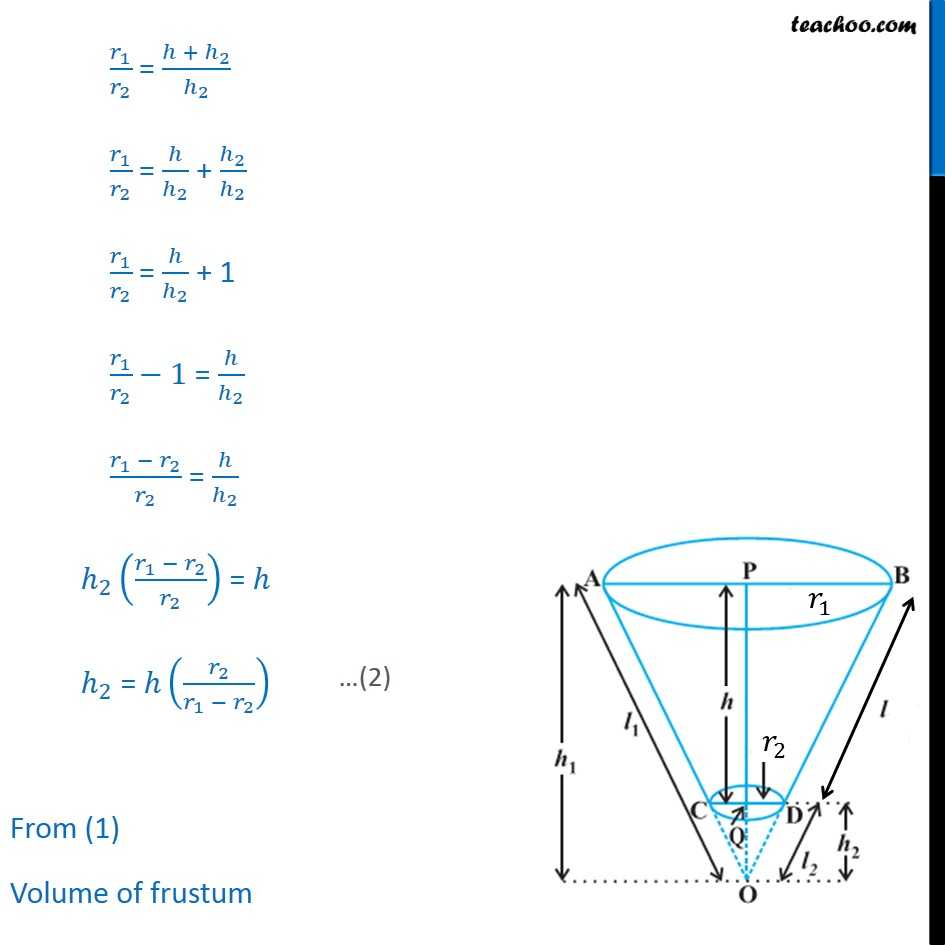
Question 7 Derive the formula for the volume of the frustum of a cone, given to you in Section 13.5, using the symbols as explained. There are two cones OCD & OAB We are given Height of frustum = h Slant height of frustum = l Radius PB = r1 Radius QD = r2 We need to find Curved Surface Area & Total Surface Area Here, We need to write h1, l1, h2, l2 in terms of h and l Volume of frustum = Volume of cone OAB Volume of cone OCD = 1/3 _1 ^2 _1 1/3 _2 ^2 _2 In OPB & OQD BOP = DOQ OPB = OQD So, OPB OQD / = / _1/ _2 = _1/ _2 Putting h1 = h + h2 _1/ _2 = ( + _2)/ _2 _1/ _2 = / _2 + _2/ _2 _1/ _2 = / _2 + 1 _1/ _2 1 = / _2 ( _1 _2)/ _2 = / _2 _2 (( _1 _2)/ _2 ) = _2 = ( _2/( _1 _2 )) From (1) Volume of frustum = 1/3 _1 ^2 _1 1/3 _2 ^2 _2 Putting h1 = h + h2 = 1/3 _1 ^2 ( + _2) 1/3 _2 ^2 _2 From (2): Putting _2 = ( _2/( _1 _2 )) = 1/3 _1 ^2 ( + ( _2/( _1 _2 ))) 1/3 _2 ^2 ( _2/( _1 _2 )) = 1/3 _1 ^2 (1+( _2/( _1 _2 ))) 1/3 _2 ^2 ( _2/( _1 _2 )) = 1/3 _1 ^2 (( _1 _2 + _2)/( _1 _2 )) 1/3 _2 ^2 ( _2/( _1 _2 )) = 1/3 _1 ^2 ( _1/( _1 _2 )) 1/3 _2 ^2 ( _2/( _1 _2 )) = 1/3 ( _1 ^3/( _1 _2 )) 1/3 ( _2 ^3/( _1 _2 )) = 1/3 (( _1 ^3 _2 ^3)/( _1 _2 )) Using a3 b3 = (a b) (a2 + b2 + ab) = 1/3 (( _1 _2 )( _1 ^2+ _2 ^2 + _1 _2 )/( _1 _2 )) = 1/3 ( _1 ^2+ _2 ^2 + _1 _2 ) Volume of frustum = 1/3 ( _1 ^2+ _2 ^2 + _1 _2 )