Law of Cosine (Cosine Law)

Transcript

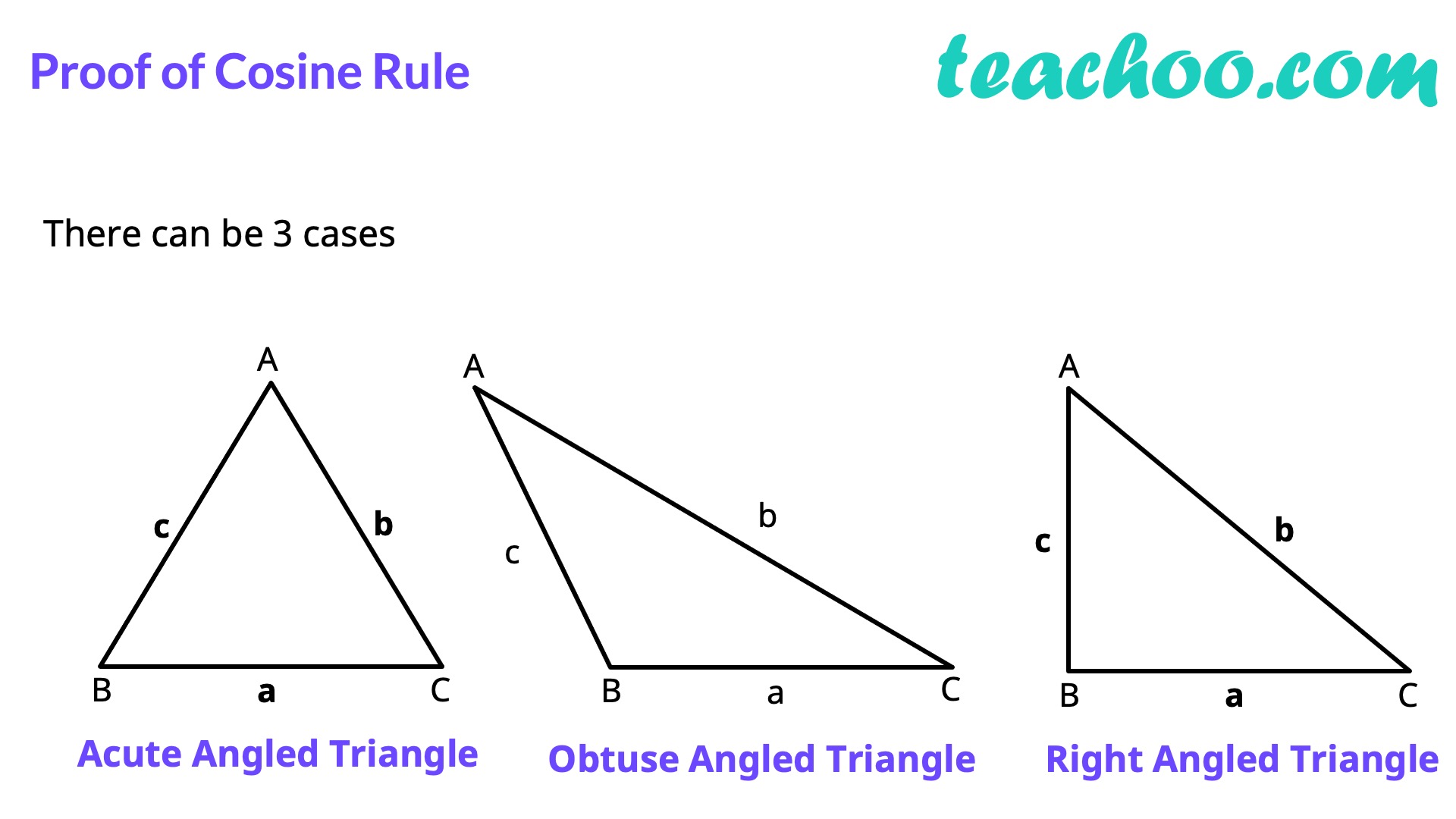
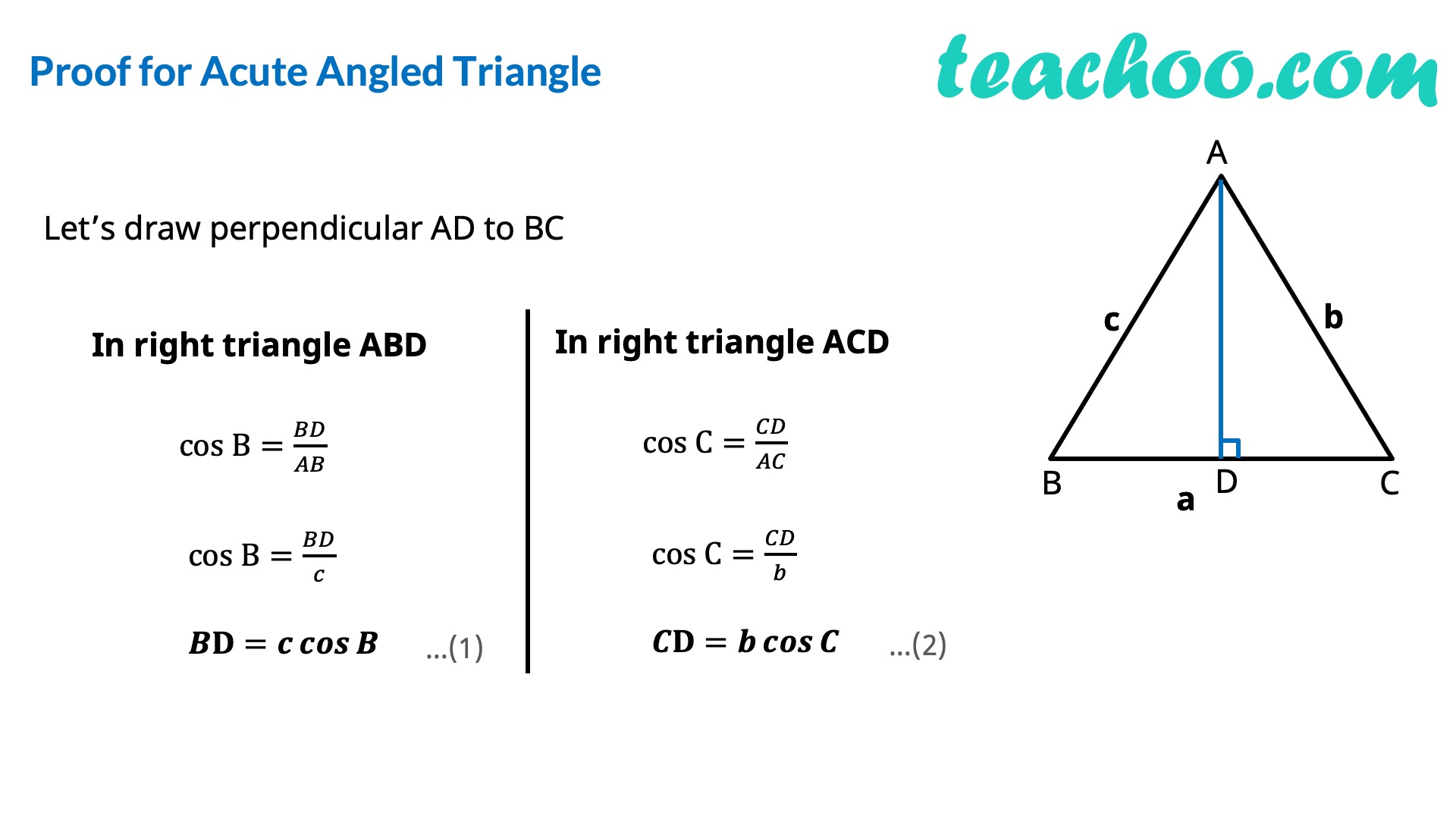
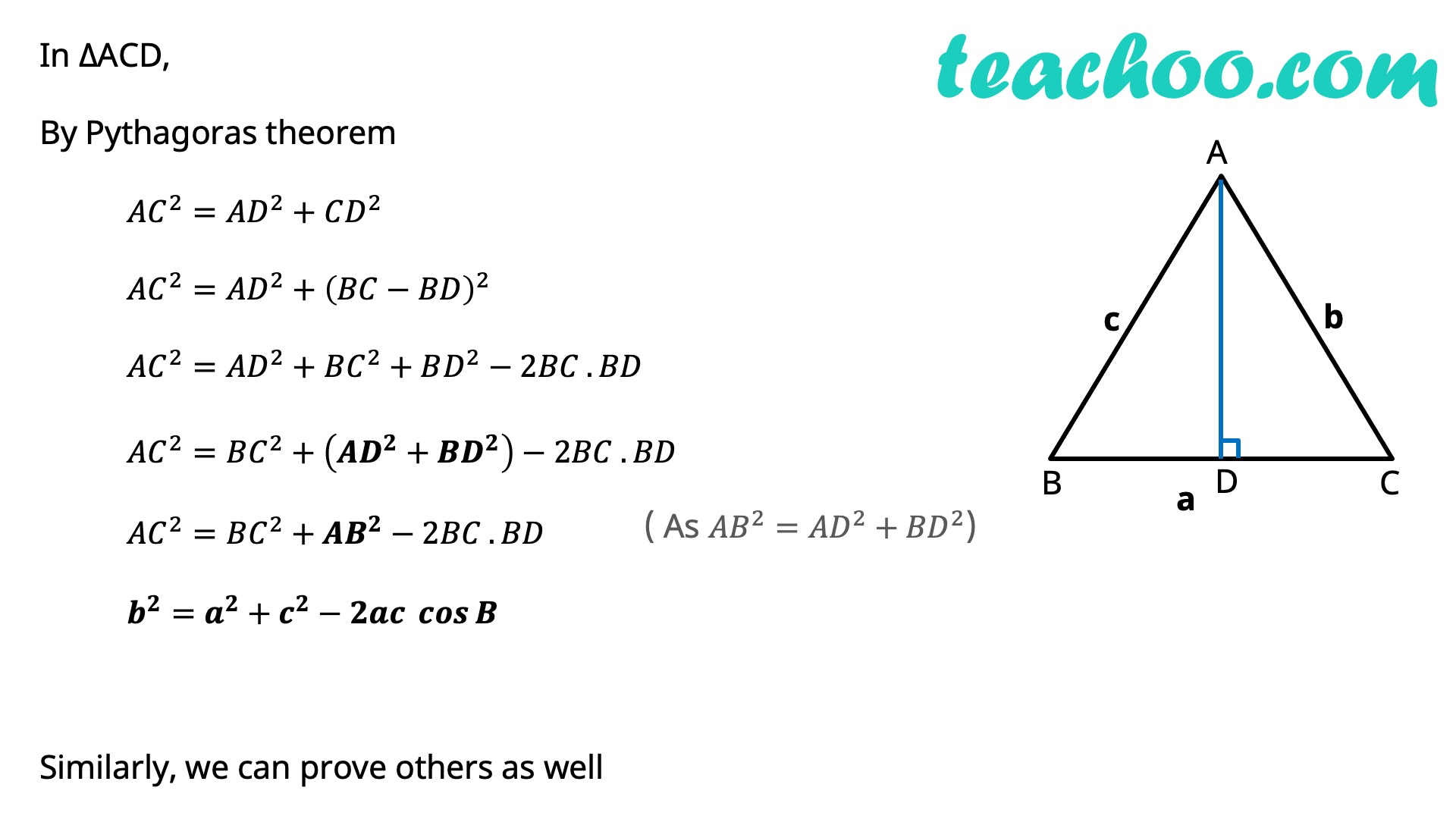
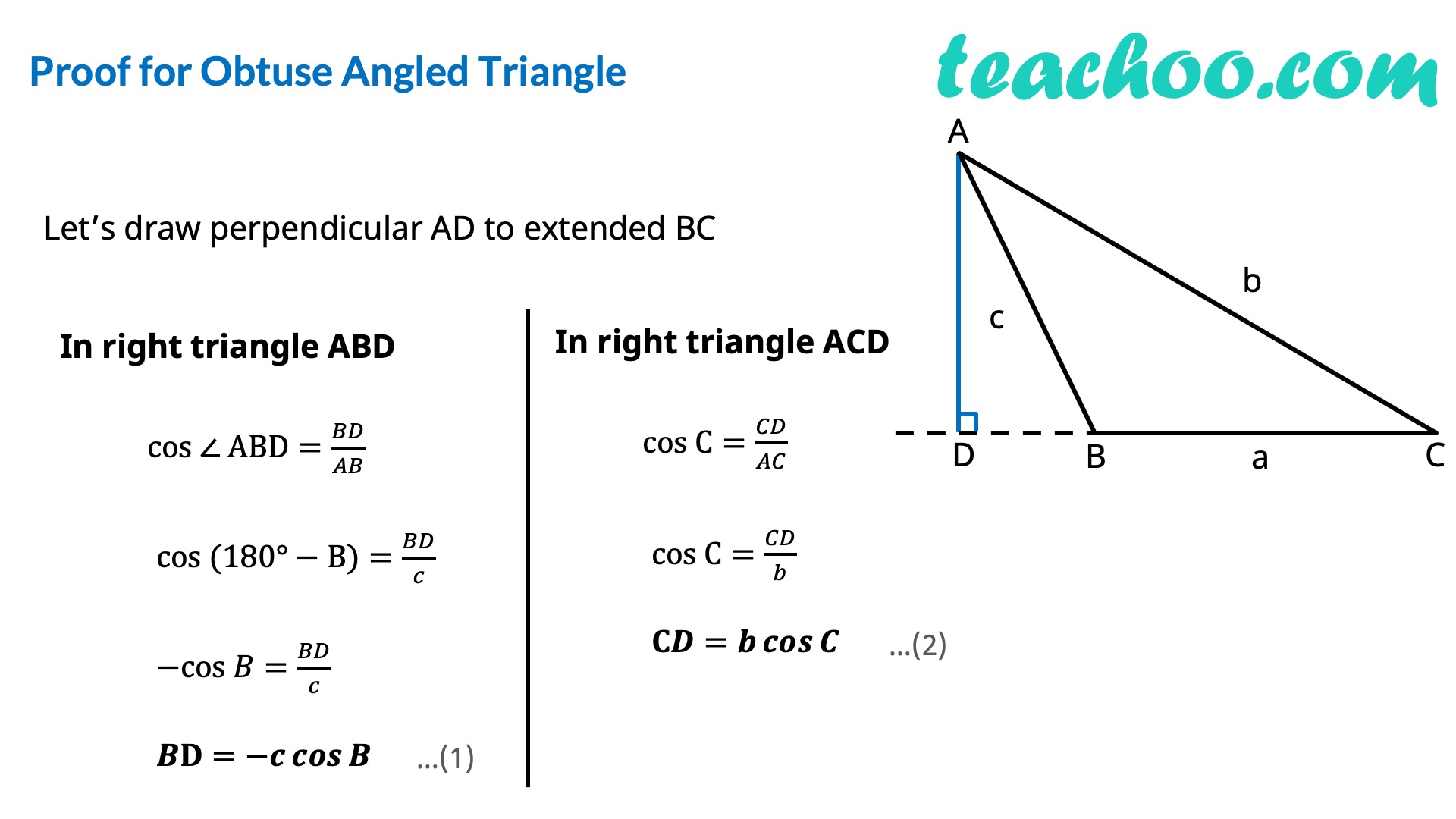
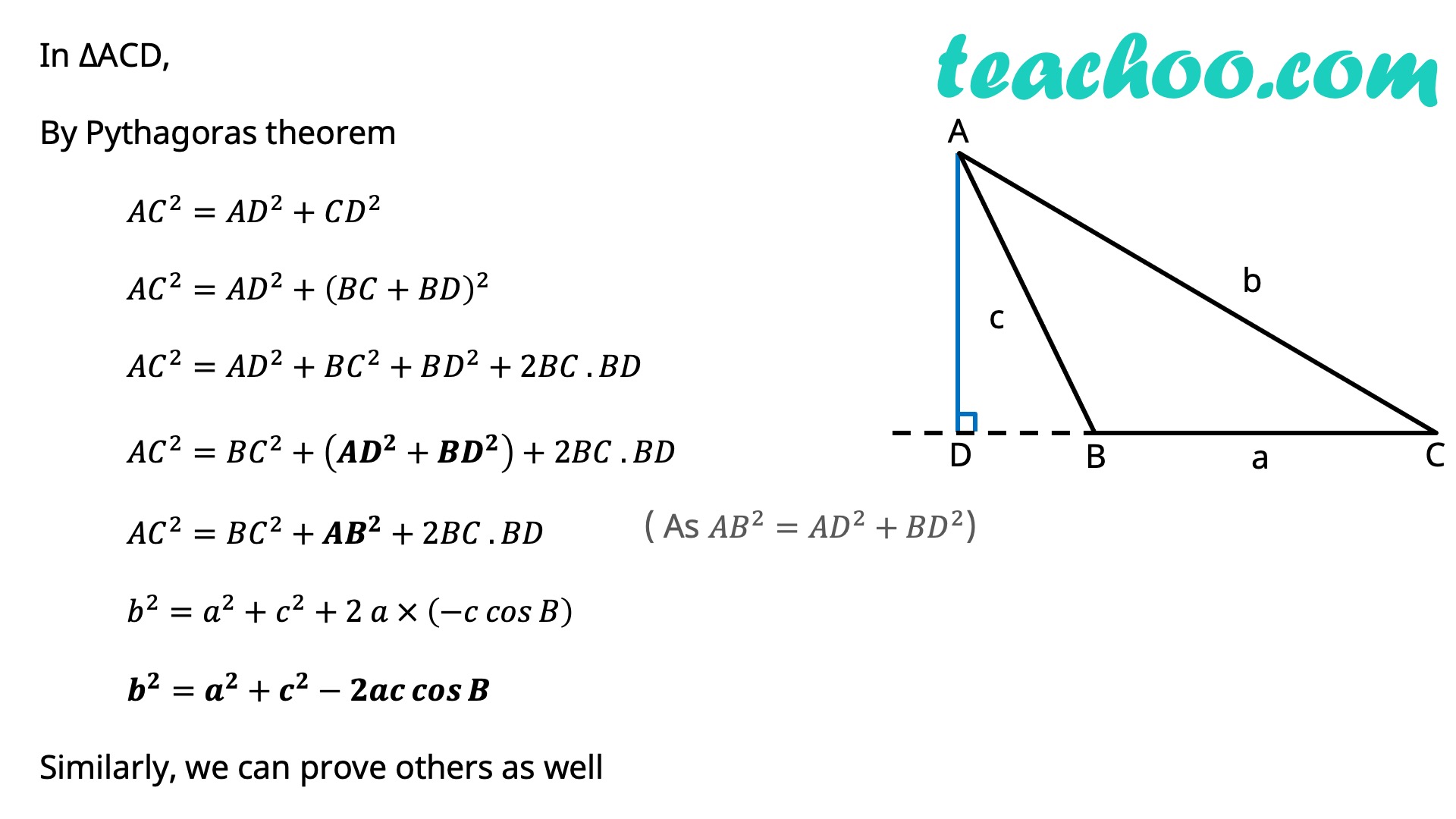
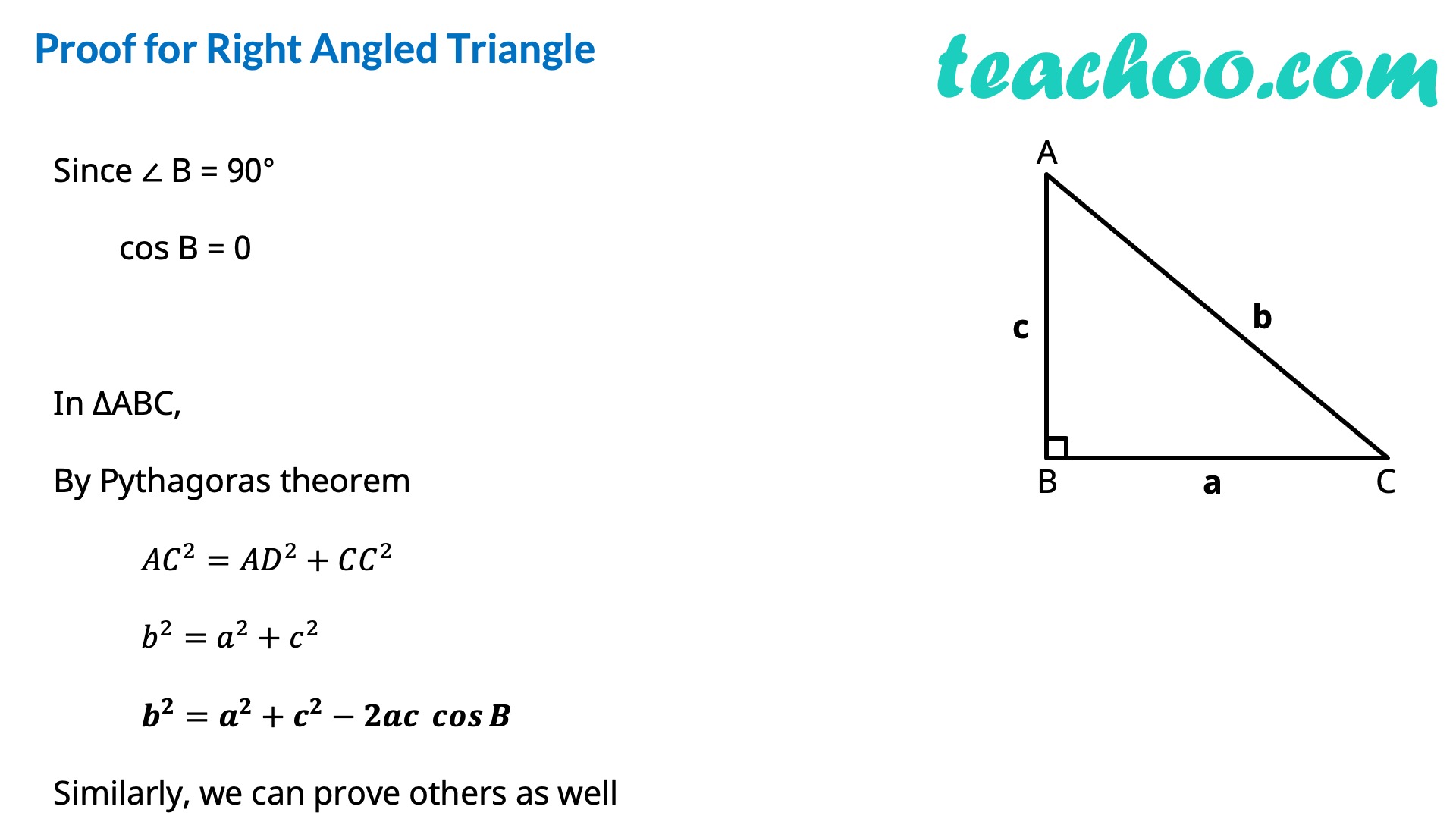
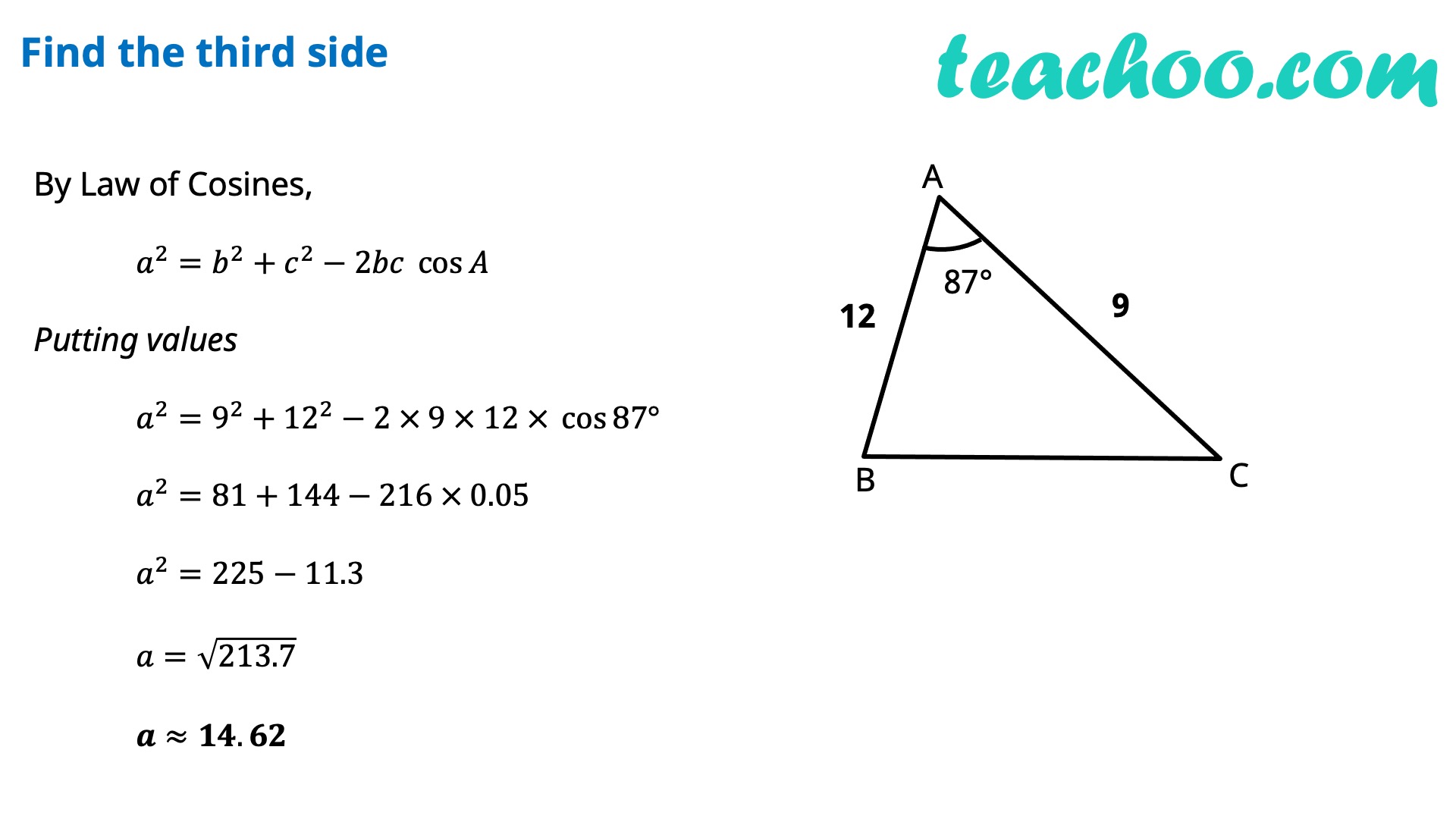
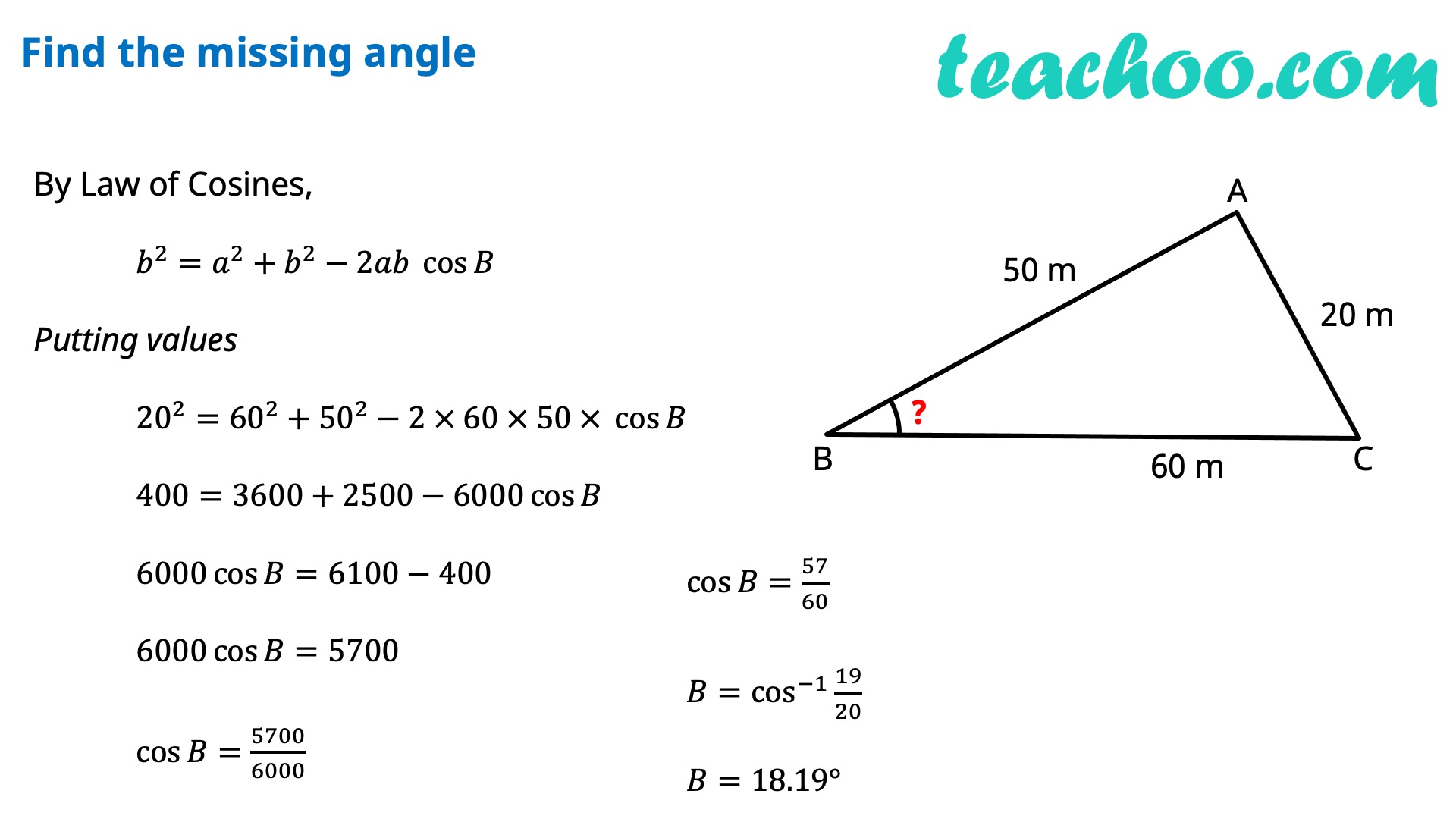
In any ∆ABC, we have 𝑎^2=𝑏^2+𝑐^2−2𝑏𝑐 cos⁡𝐴 or cos⁡𝐴=(𝑏^2 + 𝑐^2 − 𝑎^2)/2𝑏𝑐 𝑏^2=𝑐^2+𝑎^2−2𝑎𝑐 cos⁡𝐵 or cos⁡𝐵=(𝑎^2 + 𝑐^2 − 𝑏^2)/2𝑎𝑐 𝑐^2=𝑎^2+𝑏^2−2𝑎𝑏 cos⁡𝐶 or cos⁡𝐶=(𝑎^2 + 𝑏^2 − 𝑐^2)/2𝑎𝑏 Proof of Cosine Rule There can be 3 cases - Acute Angled Triangle, Obtuse Angled Triangle, Right Angled Triangle Proof for Acute Angled Triangle Let’s draw perpendicular AD to BC In right triangle ABD cos B=𝐵𝐷/𝐴𝐵 cos B=𝐵𝐷/𝑐 𝑩𝐃=𝒄 𝒄𝒐𝒔⁡𝑩 In right triangle ACD cos C=𝐶𝐷/𝐴𝐶 cos C=𝐶𝐷/𝑏 𝑪𝐃=𝒃 𝒄𝒐𝒔⁡𝑪 In ∆ACD, By Pythagoras theorem 〖𝐴𝐶〗^2=𝐴𝐷^2+𝐶𝐷^2 〖𝐴𝐶〗^2=𝐴𝐷^2+(𝐵𝐶−𝐵𝐷)^2 〖𝐴𝐶〗^2=𝐴𝐷^2+𝐵𝐶^2+𝐵𝐷^2−2𝐵𝐶 . 𝐵𝐷 〖𝐴𝐶〗^2=𝐵𝐶^2+(𝑨𝑫^𝟐+𝑩𝑫^𝟐 )−2𝐵𝐶 . 𝐵𝐷 〖𝐴𝐶〗^2=𝐵𝐶^2+𝑨𝑩^𝟐−2𝐵𝐶 . 𝐵𝐷 𝒃^𝟐=𝒂^𝟐+𝒄^𝟐−𝟐𝒂𝒄 〖 𝒄𝒐𝒔〗⁡𝑩 Similarly, we can prove others as well Proof for Obtuse Angled Triangle Let’s draw perpendicular AD to extended BC In right triangle ABD cos ∠ ABD=𝐵𝐷/𝐴𝐵 cos (180°−B)=𝐵𝐷/𝑐 −cos 𝐵=𝐵𝐷/𝑐 𝑩𝐃=−𝒄 𝒄𝒐𝒔⁡𝑩 In right triangle ACD cos C=𝐶𝐷/𝐴𝐶 cos C=𝐶𝐷/𝑏 𝐂𝑫=𝒃 𝒄𝒐𝒔⁡𝑪 In ∆ACD, By Pythagoras theorem 〖𝐴𝐶〗^2=𝐴𝐷^2+𝐶𝐷^2 〖𝐴𝐶〗^2=𝐴𝐷^2+(𝐵𝐶+𝐵𝐷)^2 〖𝐴𝐶〗^2=𝐴𝐷^2+𝐵𝐶^2+𝐵𝐷^2+2𝐵𝐶 . 𝐵𝐷 〖𝐴𝐶〗^2=𝐵𝐶^2+(𝑨𝑫^𝟐+𝑩𝑫^𝟐 )+2𝐵𝐶 . 𝐵𝐷 〖𝐴𝐶〗^2=𝐵𝐶^2+𝑨𝑩^𝟐+2𝐵𝐶 . 𝐵𝐷 𝑏^2=𝑎^2+𝑐^2+2 𝑎 × (−𝑐 𝑐𝑜𝑠⁡𝐵 ) 𝒃^𝟐=𝒂^𝟐+𝒄^𝟐−𝟐𝒂𝒄 𝒄𝒐𝒔⁡𝑩 Similarly, we can prove others as well Proof for Right Angled TriangleSince ∠ B = 90° cos B = 0 In ∆ABC, By Pythagoras theorem 〖𝐴𝐶〗^2=𝐴𝐷^2+𝐶𝐶^2 𝑏^2=𝑎^2+𝑐^2 𝒃^𝟐=𝒂^𝟐+𝒄^𝟐−𝟐𝒂𝒄 𝒄𝒐𝒔⁡𝑩 Similarly, we can prove others as well Let’s do some Examples!! Find the third side By Law of Cosines, 𝑎^2=𝑏^2+𝑐^2−2𝑏𝑐 cos⁡𝐴 Putting values 𝑎^2=9^2+12^2−2 × 9 × 12 × cos⁡〖87°〗 𝑎^2=81+144−216 × 0.05 𝑎^2=225−11.3 𝑎=√213.7 𝒂≈𝟏𝟒.𝟔𝟐 One more Example ! Find the missing angle By Law of Cosines, 𝑏^2=𝑎^2+𝑏^2−2𝑎𝑏 cos⁡𝐵 Putting values 20^2=60^2+50^2−2 × 60 × 50 × cos⁡𝐵 400=3600+2500−6000 cos⁡𝐵 6000 cos⁡𝐵=6100−400 6000 cos⁡𝐵=5700 cos⁡𝐵=5700/6000 cos⁡𝐵=57/60 𝐵=cos^(−1)⁡〖19/20〗 𝐵=18.19° When to use Sine and Cosine Rule?Sine Rule is used when we are given 2 Angles and 1 Side (ASA) 2 Sides and 1 non-included angle (SSA) Cosine Rule is used when we are given 2 Sides and 1 included angle (SAS) 3 Sides (SSS)