Question 7 - Important Coordinate Geometry Questions - Chapter 7 Class 10 Coordinate Geometry

Transcript

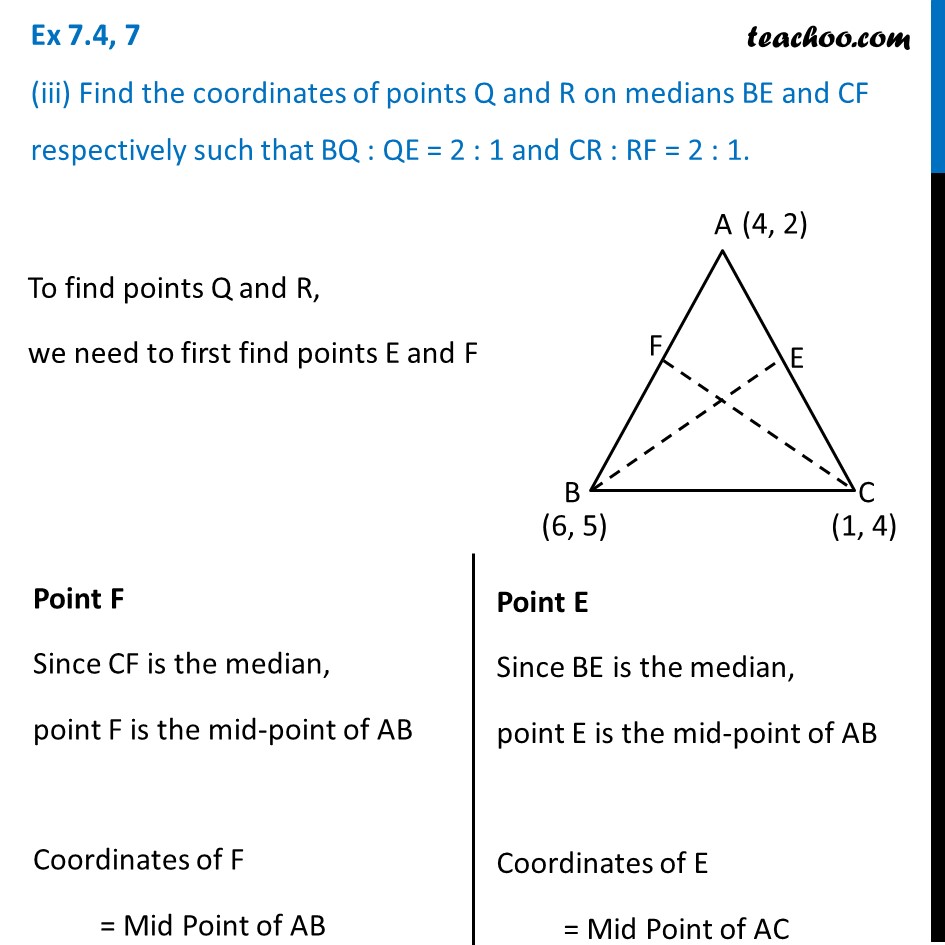
Question 7 Let A (4, 2), B(6, 5) and C(1, 4) be the vertices of Δ ABC. (i) The median from A meets BC at D. Find the coordinates of the point D. Since Median is AD D is the mid-point of BC Coordinates of D = Coordinates of mid-point of BC = ((𝑥_1 + 𝑥_2)/2, (𝑦_1 + 𝑦_2)/2) Here 𝑥_1=6 𝑦_1=5 𝑥_2=1 𝑦_2=4 Coordinates of D = ((𝑥_1 + 𝑥_2)/2, (𝑦_1 + 𝑦_2)/2) = ((6 + 1)/2, (5 + 7)/2) = (𝟕/𝟐,𝟗/𝟐) Question 7 (ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1 Point P divides AD in the ratio 2 : 1 Applying section formula, Coordinates of P are ((𝑚_1 𝑥_2 + 𝑚_2 𝑥_1)/(𝑚_1 + 𝑚_2 ), (𝑚_1 𝑦_2+ 𝑚_2 𝑦_1)/(𝑚_1 + 𝑚_2 )) Put 𝑚_1=2 𝑚_2=1 𝑥_1=4 𝑥_2=7/2 𝑦_1=2 𝑦_2=9/2 Coordinates of Point P = ((2 (7/2) + 1(4))/(2 + 1), (2 (9/2) + 1 (2))/(2 + 1)) = ((7 + 4)/3,(9 + 2)/3) = (𝟏𝟏/𝟑,𝟏𝟏/𝟑) Question 7 (iii) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1. To find points Q and R, we need to first find points E and F Point F Since CF is the median, point F is the mid-point of AB Coordinates of F = Mid Point of AB Point E Since BE is the median, point E is the mid-point of AB Coordinates of E = Mid Point of AC = ((𝑥_1 + 𝑥_2)/2, (𝑦_1 + 𝑦_2)/2) Here, 𝑥_1=4 𝑥_2=6 𝑦_1=2 𝑦_2=5 Coordinates of F = ((4 + 6)/2,(2 + 5)/2) = (10/2,7/2) = (5, 7/2) = ((𝑥_1 + 𝑥_2)/2, (𝑦_1 + 𝑦_2)/2) Here, 𝑥_1=4 𝑥_2=1 𝑦_1=2 𝑦_2=4 Coordinates of E = ((4 + 1)/2,(2 + 4)/2) = (5/2,6/2) = (5/2, 3) Now finding Points Q & R Point R Applying section formula, Coordinates of R = ((𝑚_1 𝑥_2 + 𝑚_2 𝑥_1)/(𝑚_1 + 𝑚_2 ), (𝑚_1 𝑦_2+ 𝑚_2 𝑦_1)/(𝑚_1 + 𝑚_2 )) Put 𝑚_1=2 𝑚_2=1 𝑥_1=1 𝑥_2=5 𝑦_1=4 𝑦_2=7/2 Point Q Applying section formula, Coordinates of Q = ((𝑚_1 𝑥_2 + 𝑚_2 𝑥_1)/(𝑚_1 + 𝑚_2 ), (𝑚_1 𝑦_2+ 𝑚_2 𝑦_1)/(𝑚_1 + 𝑚_2 )) Put 𝑚_1=2 𝑚_2=1 𝑥_1=6 𝑥_2=5/2 𝑦_1=5 𝑦_2=3 Coordinates of R = ((2(5)+ 1(1))/(2 + 1), (2 (7/2) + 1(4))/(2 + 1)) = ((10 + 1)/3,(7 + 4)/3) = (𝟏𝟏/𝟑,𝟏𝟏/𝟑) Coordinates of Q = (((2) (5/2)+ (1) (6))/(2 + 1), (2 (3) + 1(5))/(2 + 1)) = ((5 + 6)/3,(6 + 5)/3) = (𝟏𝟏/𝟑,𝟏𝟏/𝟑) Thus, coordinates of Q and R are (𝟏𝟏/𝟑,𝟏𝟏/𝟑) Question 7 (iv) What do you observe? [Note : The point which is common to all the three medians is called the centroid and this point divides each median in the ratio 2 : 1.] Coordinates of P, Q, and R are same, thus it is a common point to all the medians. Since Centroid of a triangle divides each median in ratio 2 : 1. So, point (11/2 ", " 11/2) is called centroid of triangle Question 7 (v) If A (𝑥_1, 𝑦_1), B (𝑥_2, 𝑦_2) and C (𝑥_3, 𝑦_3) are the vertices of Δ ABC, find the coordinates of the centroid of the triangle. Centroid of a triangle divides each median in ratio 2 : 1 Let us draw median AD Let O be the point which divides AD in the ratio 2 : 1 So, O is the centroid. Finding coordinates of point D Since AD is the median, D is the mid-point of BC Coordinates of D = ((𝑥_2 +〖 𝑥〗_3)/2, (𝑦_2 + 𝑦_3)/2) Now, O divides AD in the ratio 2 : 1 Using Section Formula, Coordinates of O are ((𝑚_1 𝑎_2 + 𝑚_2 𝑎_1)/(𝑚_1 + 𝑚_2 ), (𝑚_1 𝑏_2 + 𝑚_2 𝑏_1)/(𝑚_1 + 𝑚_2 )) Where A (𝑎_1, 𝑏_1) and D (𝑎_2, 𝑏_2) Here 𝑎_1=𝑥_1 𝑏_1= 𝑦_1 𝑎_2=(𝑥_2 + 𝑥_3)/2 𝑏_2=(𝑦_2 + 𝑦_3)/2 𝑚_1=2 𝑚_2=1 Coordinates of O = (((2) ((𝑥_2 + 𝑥_3)/2) + (1) (𝑥_1 ))/(2 + 1),((2) ((𝑦_2 + 𝑦_3)/2) + (1) (𝑦_1 ))/(2 + 1)) =((𝑥_2 +〖 𝑥〗_3 + 𝑥_1)/3, (𝑦_2 + 𝑦_3 + 𝑦_1)/3) = ((𝒙_𝟏 +〖 𝒙〗_𝟐 + 𝒙_𝟑)/𝟑, (𝒚_𝟏 + 𝒚_𝟐 + 𝒚_𝟑)/𝟑) Note :- If we would have used section formula in CF or BE, we would have got the same result.