Question 6 - Important Coordinate Geometry Questions - Chapter 7 Class 10 Coordinate Geometry

Transcript

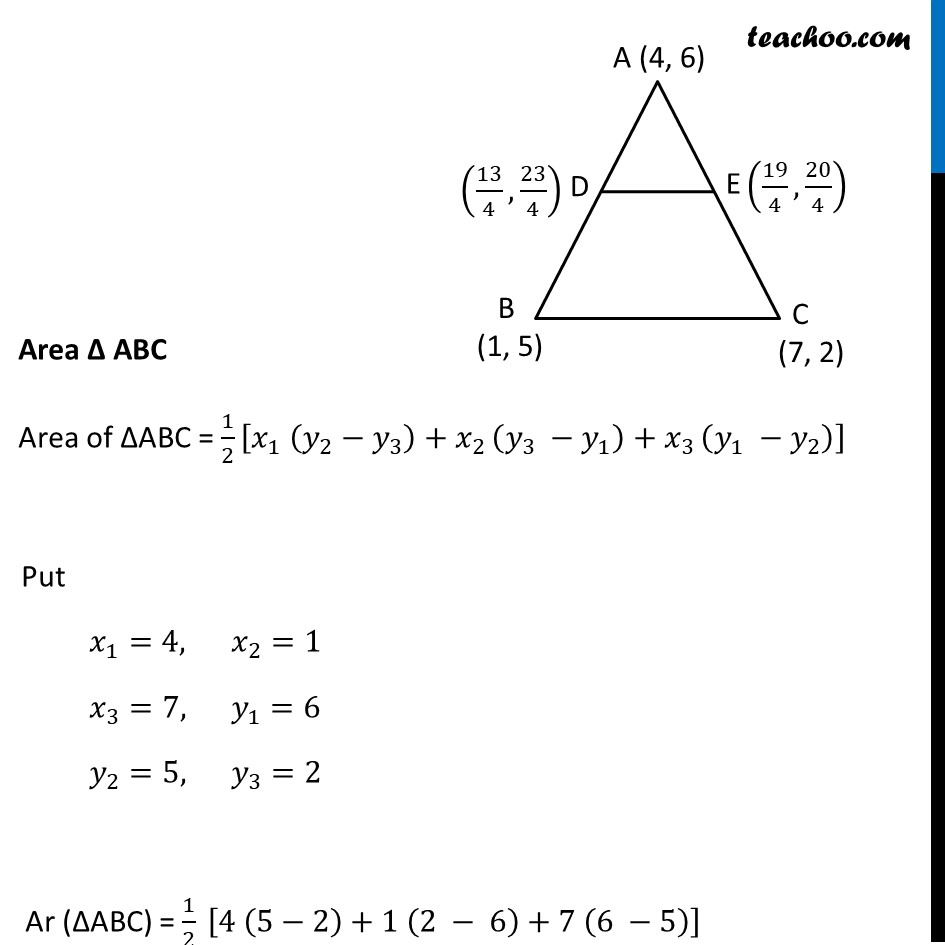
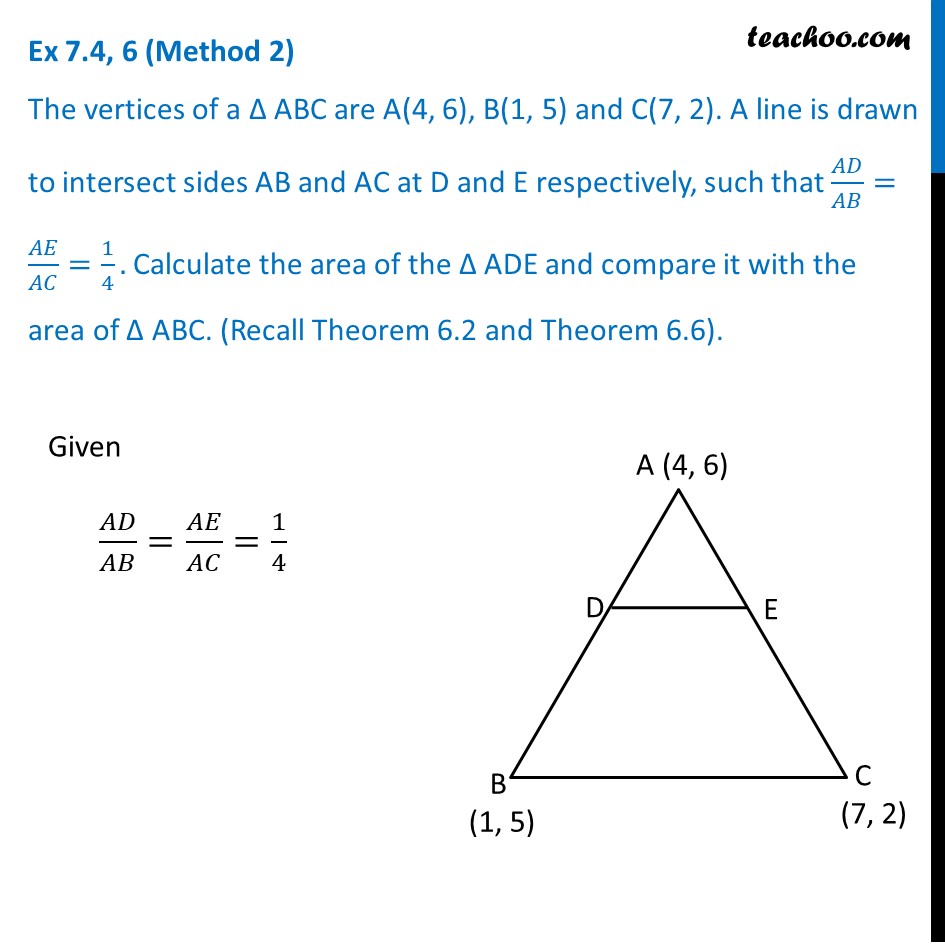
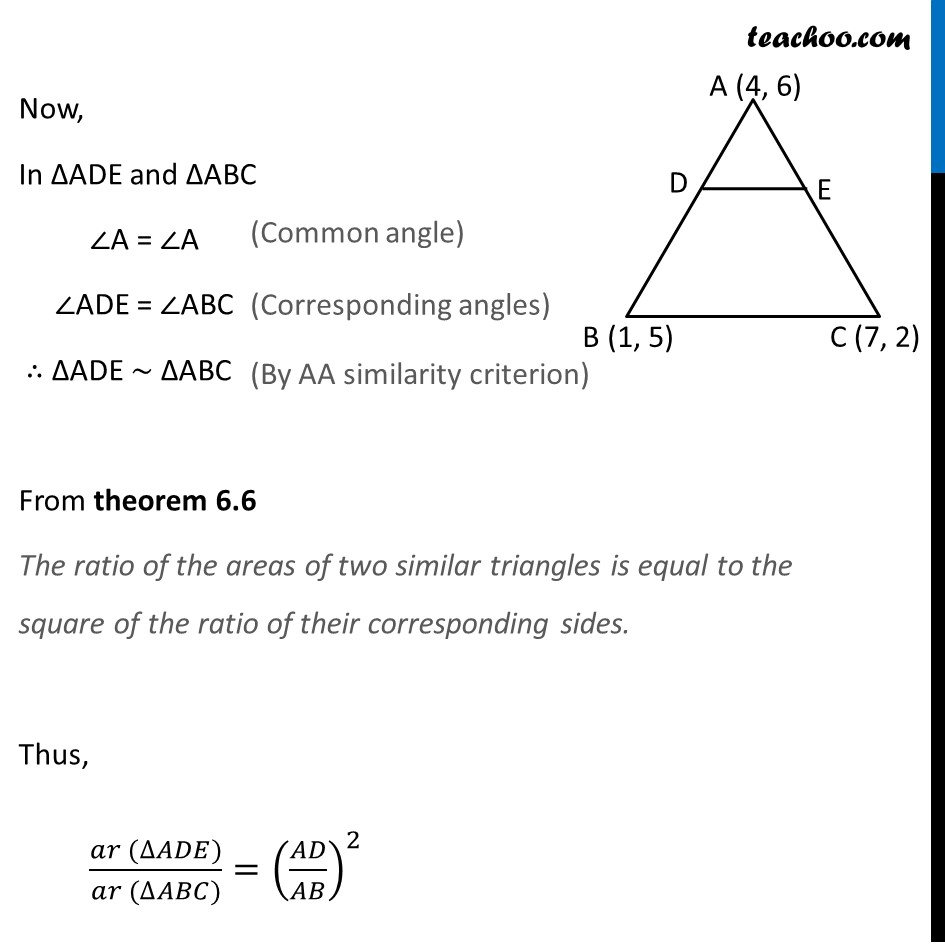
Question 6 (Method 1) The vertices of a Δ ABC are A(4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that 𝐴𝐷/𝐴𝐵=𝐴𝐸/𝐴𝐶=1/4. Calculate the area of the Δ ADE and compare it with the area of Δ ABC. (Recall Theorem 6.2 and Theorem 6.6). Given 𝐴𝐷/𝐴𝐵=𝐴𝐸/𝐴𝐶=1/4 𝑨𝑫/𝑨𝑩=𝟏/𝟒 𝑨𝑬/𝑨𝑪=𝟏/𝟒 4 AD = AB 4 AD = AD + BD 4 AD − AD = BD 3 AD = BD 𝐴𝐷/𝐵𝐷=1/3 Thus point D divides AB in the ratio 1 : 3. Using section formula, coordinates of D are ((𝑚_1 𝑥_2 + 𝑚_2 𝑥_1)/(𝑚_1 + 𝑚_2 ),(𝑚_1 𝑦_2 + 𝑚_2 𝑦_1)/(𝑚_1 + 𝑚_2 )) 4 AE = AC 4 AE = AE + CE 4 AE − AE = CE 3 AE = CE 𝐴𝐸/𝐶𝐸=1/3 Thus point E divides AC in the ratio 1 : 3. Using section formula, coordinates of E are ((𝑚_1 𝑥_2 + 𝑚_2 𝑥_1)/(𝑚_1 + 𝑚_2 ),(𝑚_1 𝑦_2 + 𝑚_2 𝑦_1)/(𝑚_1 + 𝑚_2 )) Put 𝑚_1=1, 𝑚_2=3 𝑥_1=4, 𝑥_2=1 𝑦_1=6, 𝑦_2=5 Point D = ((1(1) + (3)(4))/(1 + 3), (1(5) + 3(6))/(1 + 3)) = ((1 + 12)/4,(5 + 18)/4) = (13/4,23/4) Put 𝑚_1=1, 𝑚_2=3 𝑥_1=4, 𝑥_2=7 𝑦_1=6, 𝑦_2=2 Point E = ((1(7) + (3)(4))/(1 + 3), (1(2) + 3(6))/(1 + 3)) = ((7 + 12)/4,(2 + 18)/4) = (19/4,20/4) Now, finding Area of Δ ADE and Δ ABC Area Δ ADE Area of ∆ADE = 1/2 [𝑥_1 (𝑦_2−𝑦_3 )+𝑥_(2 ) (𝑦_3 −𝑦_1 )+𝑥_(3 ) (𝑦_1 −𝑦_2 )] Put 𝑥_1=4, 𝑥_2=13/4 𝑥_3=19/4, 𝑦_1=6 𝑦_2=23/4, 𝑦_3=20/4 𝑦_2=23/4, 𝑦_3=20/4 Ar (∆ADE) = 1/2 [4 (23/4−20/4)+13/4 (20/4−6)+19/4 (6 −23/4)] = 1/2 [4 (3/4)+13/4 ((20 − 24)/4)+19/4 ((24 − 23)/4)] = 1/2 [4 (3/4)+13/4 ((−4)/4)+19/4 (1/4)] = 1/2 [12/4−52/16+19/16] = 1/2 [(48 − 52 + 19)/16] = 𝟏𝟓/𝟑𝟐 sq. units. Area Δ ABC Area of ∆ABC = 1/2 [𝑥_1 (𝑦_2−𝑦_3 )+𝑥_(2 ) (𝑦_3 −𝑦_1 )+𝑥_(3 ) (𝑦_1 −𝑦_2 )] Put 𝑥_1=4, 𝑥_2=1 𝑥_3=7, 𝑦_1=6 𝑦_2=5, 𝑦_3=2 Ar (∆ABC) = 1/2 [4 (5−2)+1 (2 − 6)+7 (6 −5)] = 1/2 [4 (3)+1 (−4)+7 (1)] = 1/2 [12 − 4+7] = 15/2 sq. units. Thus, (𝑎𝑟 (∆𝐴𝐷𝐸))/(𝑎𝑟 (∆𝐴𝐵𝐶))=(15/32)/(15/2) = 15/32×2/15 = 1/16 Thus, area of ∆ADE is 𝟏𝟓/𝟑𝟐 sq. units and (𝑎𝑟 (∆𝐴𝐷𝐸))/(𝑎𝑟 (∆𝐴𝐵𝐶))=𝟏/𝟏𝟔 Question 6 (Method 2) The vertices of a Δ ABC are A(4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that 𝐴𝐷/𝐴𝐵=𝐴𝐸/𝐴𝐶=1/4. Calculate the area of the Δ ADE and compare it with the area of Δ ABC. (Recall Theorem 6.2 and Theorem 6.6). Given 𝐴𝐷/𝐴𝐵=𝐴𝐸/𝐴𝐶=1/4 𝑨𝑫/𝑨𝑩=𝟏/𝟒 4 AD = AB 4 AD = AD + BD 4 AD − AD = BD 3 AD = BD 𝐴𝐷/𝐵𝐷=1/3 𝑨𝑬/𝑨𝑪=𝟏/𝟒 4 AE = AC 4 AE = AE + CE 4 AE − AE = CE 3 AE = CE 𝐴𝐸/𝐶𝐸=1/3 Thus, 𝐴𝐷/𝐴𝐵=𝐴𝐸/𝐴𝐶=1/3 ∴ DE divides AB and AC in the ratio 1 : 3 Applying theorem 6.2, DE ∥ BC From theorem 6.2 If a line divides any two sides of a triangle in the same ratio, then it is parallel to the third side. Now, In ∆ADE and ∆ABC ∠A = ∠A ∠ADE = ∠ABC ∴ ∆ADE ~ ∆ABC From theorem 6.6 The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Thus, (𝑎𝑟 (∆𝐴𝐷𝐸))/(𝑎𝑟 (∆𝐴𝐵𝐶))=(𝐴𝐷/𝐴𝐵)^2 (Common angle) (Corresponding angles) (By AA similarity criterion) (𝑎𝑟 (∆𝐴𝐷𝐸))/(𝑎𝑟 (∆𝐴𝐵𝐶))=(1/4)^2=1/16 𝑎𝑟 (∆𝐴𝐷𝐸)=1/16 𝑎𝑟 (∆𝐴𝐵𝐶) Now, Finding Area Δ ABC 𝑎𝑟 (∆𝐴𝐵𝐶)=1/2 [𝑥_1 (𝑦_2−𝑦_3 ) + 𝑥_2 (𝑦_3−𝑦_1 ) + 𝑥_3 (𝑦_1−𝑦_2 )] Put 𝑥_1=4, 𝑦_1=6 𝑥_2=1, 𝑦_2=5 𝑥_3=7, 𝑦_3=2 Ar (∆ABC) = 1/2 [4 (5−2)+1 (2 − 6)+7 (6 −5)] = 1/2 [4 (3)+1 (−4)+7 (1)] = 1/2 [12 − 4+7] = 15/2 sq. units. Thus, From (1) ar (∆ADE) = 1/16 ar (∆ABC) = 1/16×15/2=15/32 sq. units. Thus, area of ∆ADE is 𝟏𝟓/𝟑𝟐 sq. units and (𝑎𝑟 (∆𝐴𝐷𝐸))/(𝑎𝑟 (∆𝐴𝐵𝐶))=𝟏/𝟏𝟔