You are here
Question 9 - Important questions of Triangle (in Geometry) - Chapter 6 Class 10 Triangles
Last updated at August 8, 2026 by Teachoo
Important questions of Triangle (in Geometry)
Chapter 6 Class 10 Triangles
Serial order wise
- Ex 6.1
- Ex 6.2
- Ex 6.3
- Examples
- Theorems
- Case Based Questions (MCQ)
- NCERT Exemplar - MCQ
- Ratio of Area of Similar Triangles
- Pythagoras Theorem and it's important questions
-
Important questions of Triangle (in Geometry)
Take a fresh quiz. Then take another.
Every attempt is a new AI-adaptive Teachoo quiz with 3 questions, selected from your answers, mistakes, and progress.
Transcript
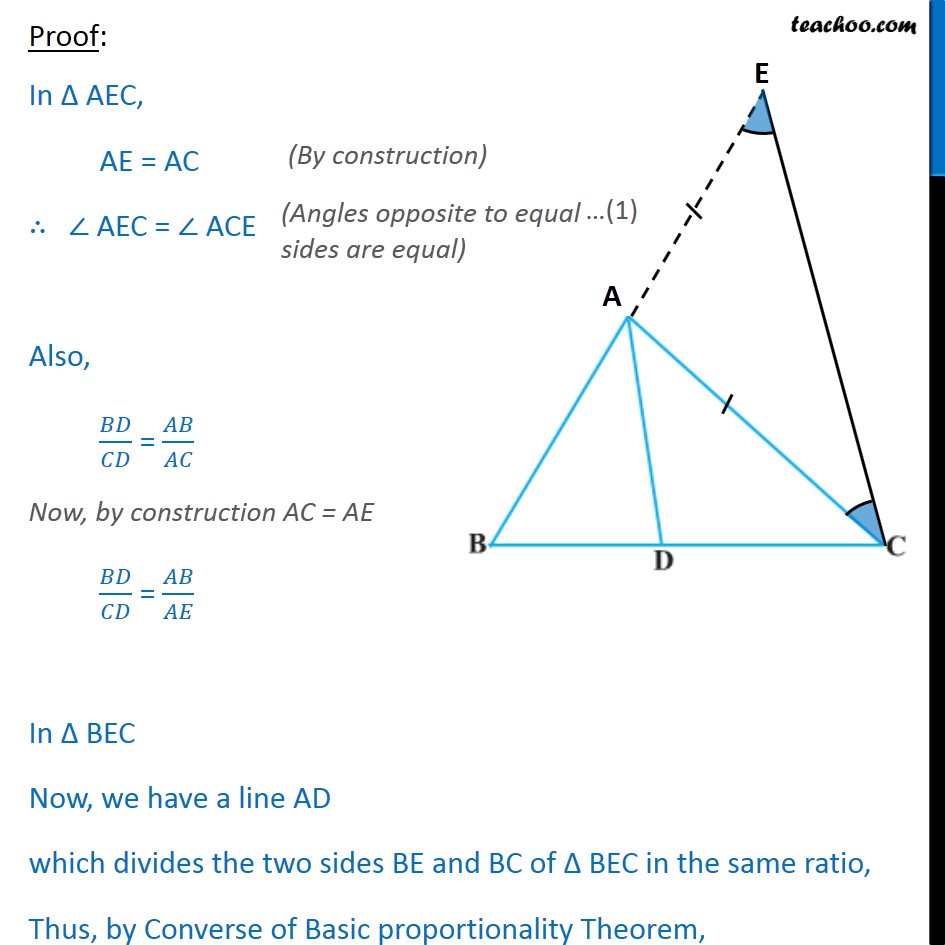
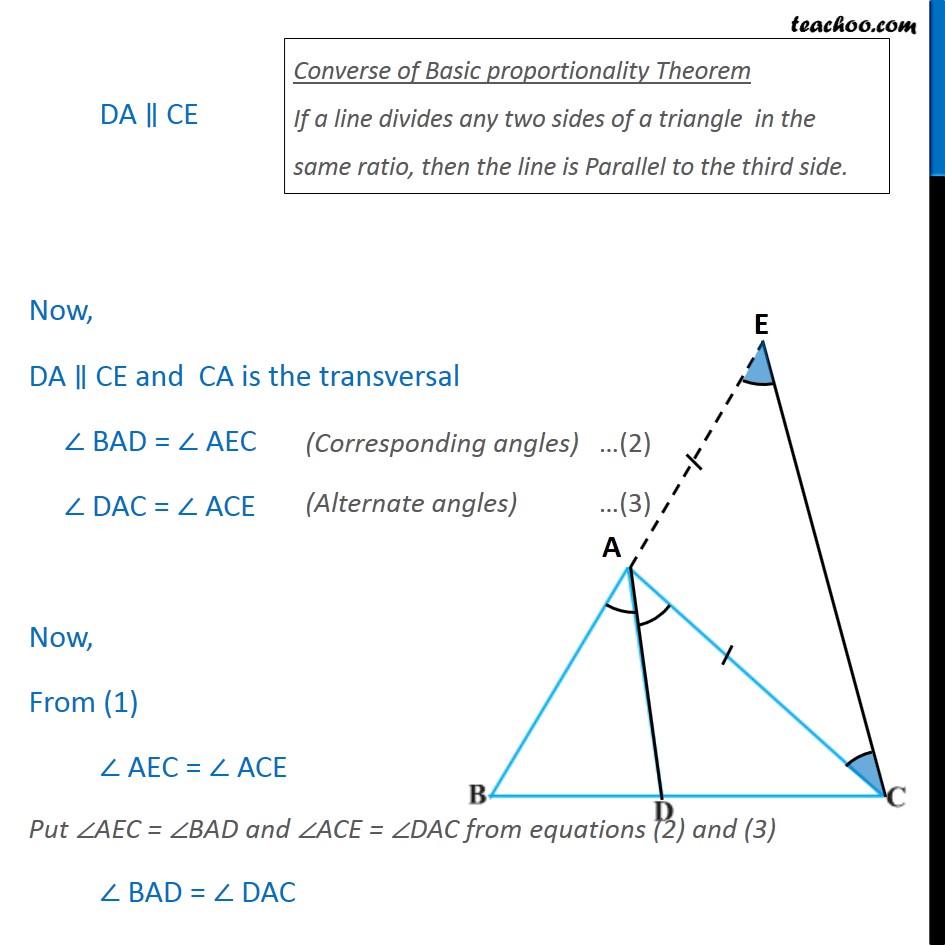
Question 9 In Fig. 6.63, D is a point on side BC of ABC such that / = / Prove that AD is the bisector of BAC. Given : A ABC Where / = / To Prove: AD is the bisector of BAC i.e. BAD = DAC Construction : Produce BA to E such that AE = AC. Now join CE. Proof: In AEC, AE = AC AEC = ACE Also, / = / Now, by construction AC = AE / = / In BEC Now, we have a line AD which divides the two sides BE and BC of BEC in the same ratio, Thus, by Converse of Basic proportionality Theorem,DA CE Now, DA CE and CA is the transversal BAD = AEC DAC = ACE Now, From (1) AEC = ACE Put AEC = BAD and ACE = DAC from equations (2) and (3) BAD = DAC Converse of Basic proportionality Theorem If a line divides any two sides of a triangle in the same ratio, then the line is Parallel to the third side. Thus, AD is the bisector of BAC Hence proved
