Question 6 - Important questions of Triangle (in Geometry) - Chapter 6 Class 10 Triangles

Transcript

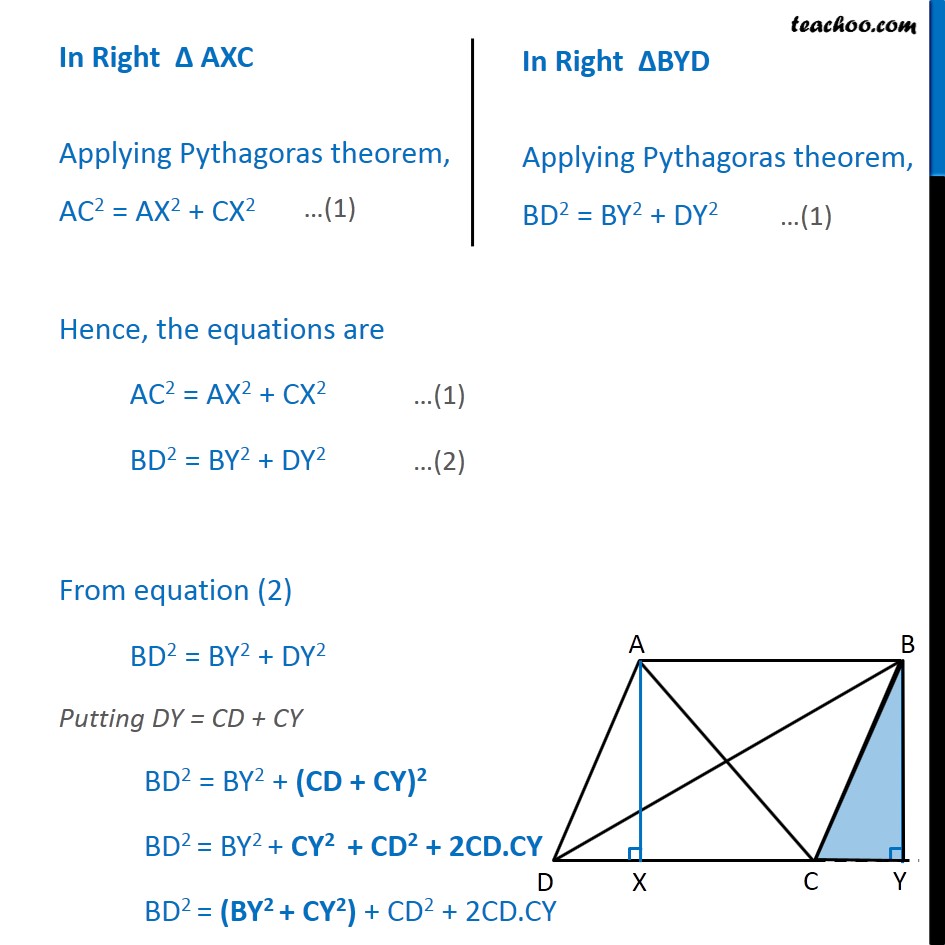
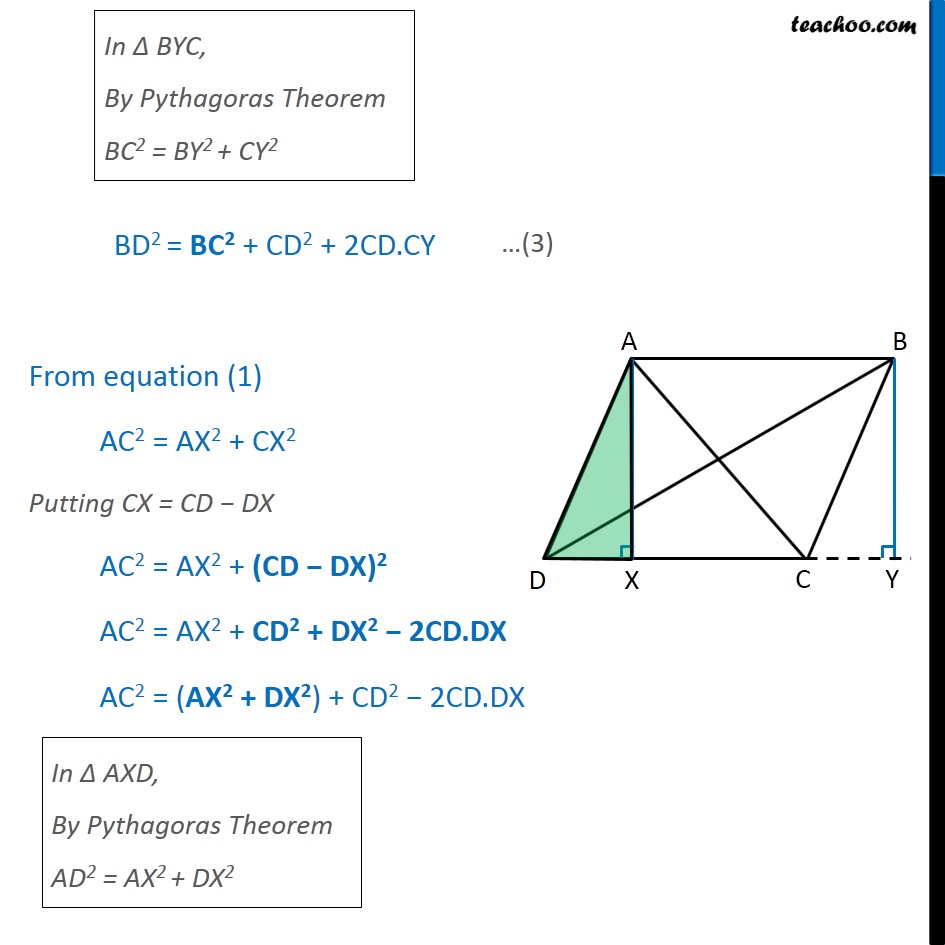
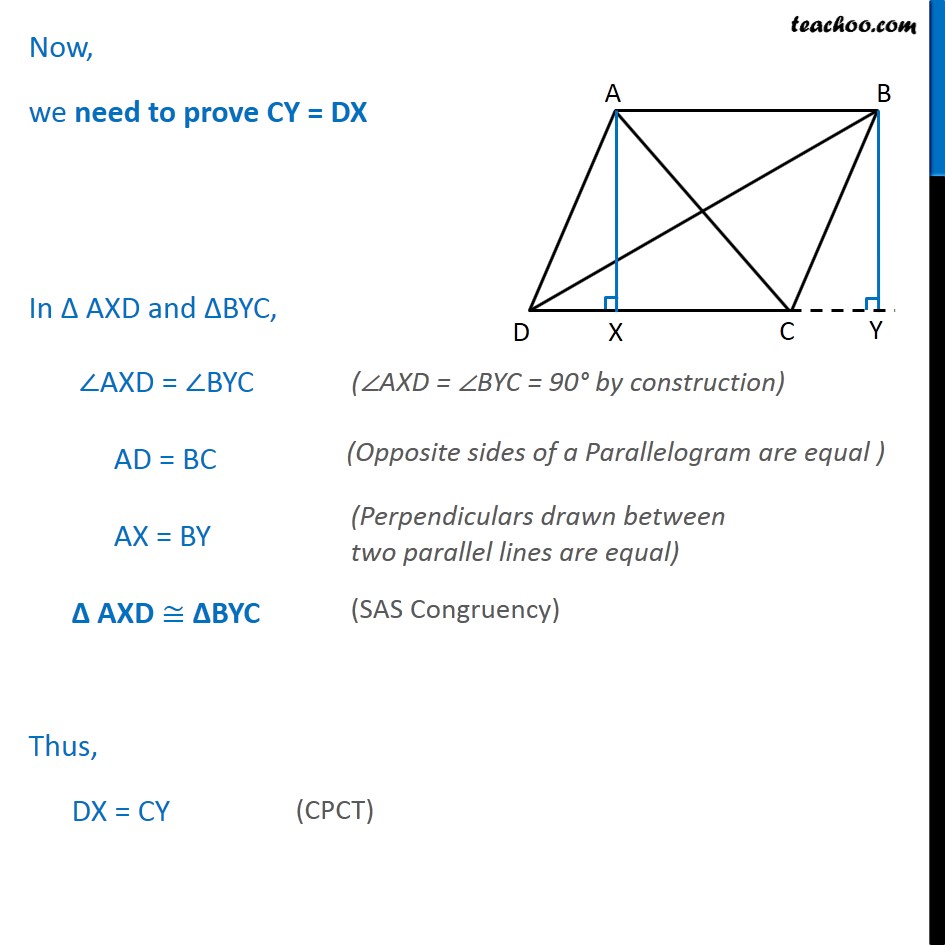
Question 6 Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides. Given: ABCD is a parallelogram To Prove: Sum of squares of diagonals = Sum of squares of its sides AC2 + BD2 = AB2 + BC + CD2 + DA2 Construction: Draw AX CD and BY DC extended to Y. Proof: In Right AXC Applying Pythagoras theorem, AC2 = AX2 + CX2 In Right BYD Applying Pythagoras theorem, BD2 = BY2 + DY2 In BYC, By Pythagoras Theorem BC2 = BY2 + CY2 BD2 = BC2 + CD2 + 2CD.CY From equation (1) AC2 = AX2 + CX2 Putting CX = CD DX AC2 = AX2 + (CD DX)2 AC2 = AX2 + CD2 + DX2 2CD.DX AC2 = (AX2 + DX2) + CD2 2CD.DX In AXD, By Pythagoras Theorem AD2 = AX2 + DX2 In parallelogram ABCD, Opposite sides of parallelogram are equal CD = AB AC2 = AD2 + CD2 2CD.DX AC2 = AD2 + AB2 2CD.DX Hence, the equations are BD2 = BC2 + CD2 + 2CD.CY (3) AC2 = AD2 + AB2 2CD.DX (4) Adding equations (3) and (4) BD2 + AC2 = BC2 + CD2 + 2CD.CY + AD2 + AB2 2CD.DX BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD(CY DX) Now, we need to prove CY = DX In AXD and BYC, AXD = BYC AD = BC AX = BY AXD BYC Thus, DX = CY Putting CY = DX in equation (5) BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (CY DX) BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD (DX DX) BD2 + AC2 = BC2 + CD2 + AD2 + AB2 + 2CD 0 BD2 + AC2 = BC2 + CD2 + AD2 + AB2 Hence Proved