Example 5 (Optional) - Chapter 2 Class 10 Polynomials

Transcript

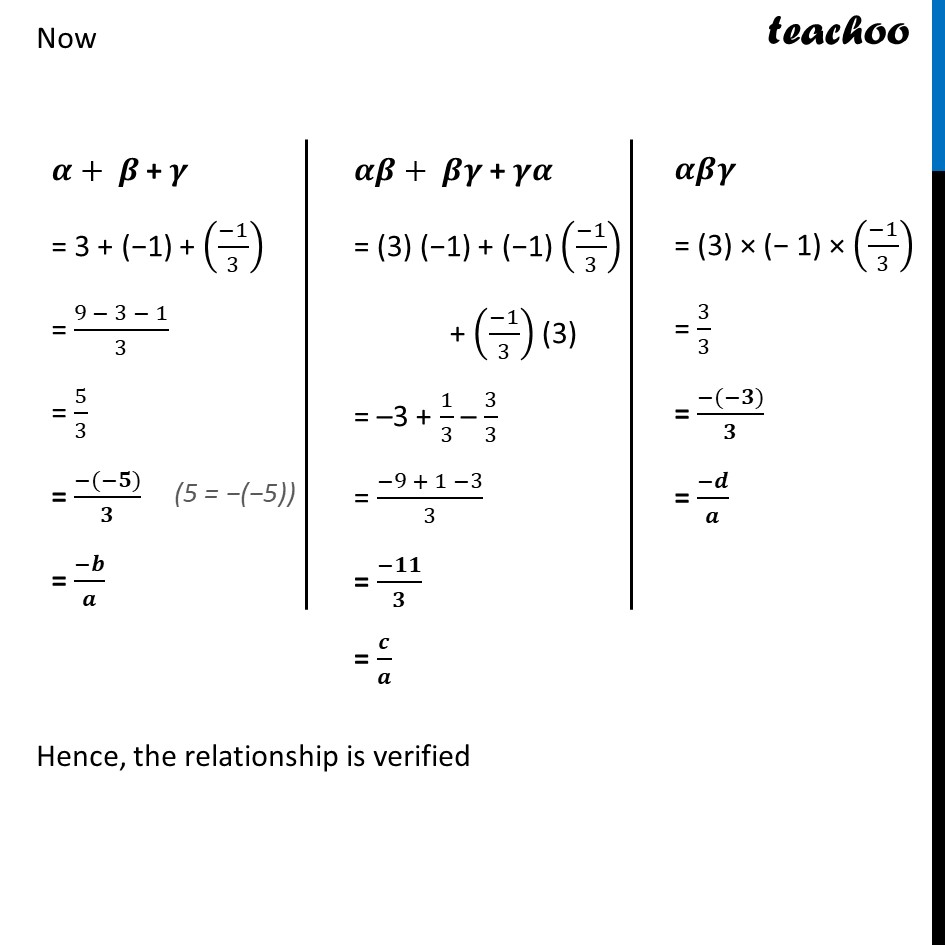
Example 5 Verify that 3, –1, (−1)/3 are the zeroes of the cubic polynomial p(x) = 3x3 – 5x2 – 11x – 3, and then verify the relationship between the zeroes and the coefficients. p(x) = 3x3 − 5x2 − 11x − 3 Verifying zeroes At x = 3, p(3) = 3 (3)3 − 5(3)2 − 11(3) − 3 = 81 − 45 − 33 − 3 = 0 Since p(3) = 0 Hence, 3 is a zero of p(x) At x = −1, p(−1) = 3 (-1)3 − 5(-1)2 − 11 (-1) − 3 = −3 − 5 + 11 − 3 = 0 Since p(−1) = 0 Hence, −1 is a zero of p(x) At x = (−𝟏)/𝟑 p((−1)/3) = 3((−1)/3)^3− 5((−1)/3)^2 − 11 ((−1)/3) − 3 = (−1)/9 − 5/9 + 11/3 − 3 = (−1 − 5 + 33 − 27)/9 = (−33+33)/9 = 0 Since p((−𝟏)/𝟑) = 0. Hence, (−𝟏)/𝟑 is a zero of P (x) Verifying relationship between zeroes and coefficients. For p(x) = 3x3 − 5x2 − 11x − 3, a = 3, b = −5, c = −11 and d = −3 And zeroes are 𝜶 = 3, 𝛽 = −1 and 𝜸 = (−𝟏)/𝟑 For a cubic Polynomial p(x) = ax3 + bx2 + cx + d With zeroes α, 𝛽 and γ We have α + 𝛽 + γ = (−𝑏)/𝑎 α"𝛽" + 𝛽γ + γα = 𝑐/𝑎 α"𝛽" γ= (−𝑑)/𝑎 𝜶+ 𝜷 + 𝜸 = 3 + (−1) + ((−1)/3) = (9 − 3 − 1)/3 = 5/3 = (−(−𝟓))/𝟑 = (−𝒃)/𝒂 𝜶𝜷+ 𝜷𝜸 + 𝜸𝜶 = (3) (−1) + (−1) ((−1)/3) + ((−1)/3) (3) = –3 + 1/3 – 3/3 = (−9 + 1 −3)/3 = (−𝟏𝟏)/𝟑 = 𝒄/𝒂 𝜶𝜷𝜸 = (3) × (− 1) × ((−1)/3) = 3/3 = (−(−𝟑))/𝟑 = (−𝒅)/𝒂 Now Hence, the relationship is verified