




Last updated at December 16, 2024 by Teachoo









Transcript
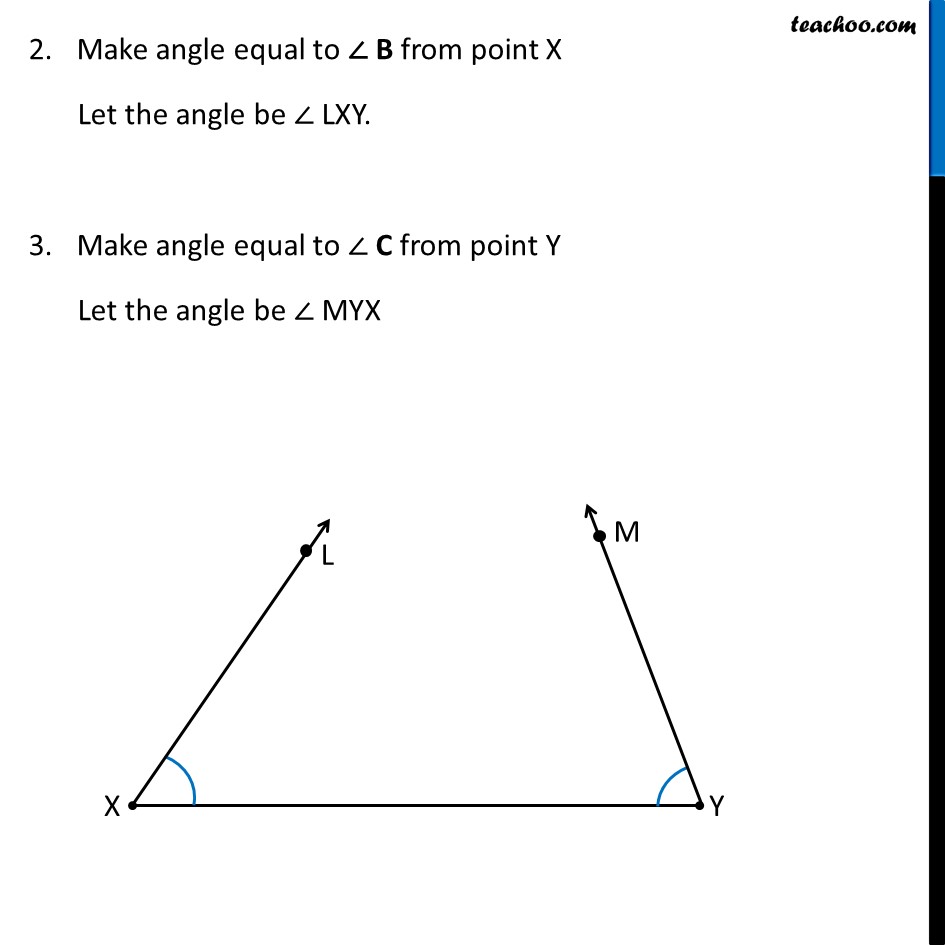
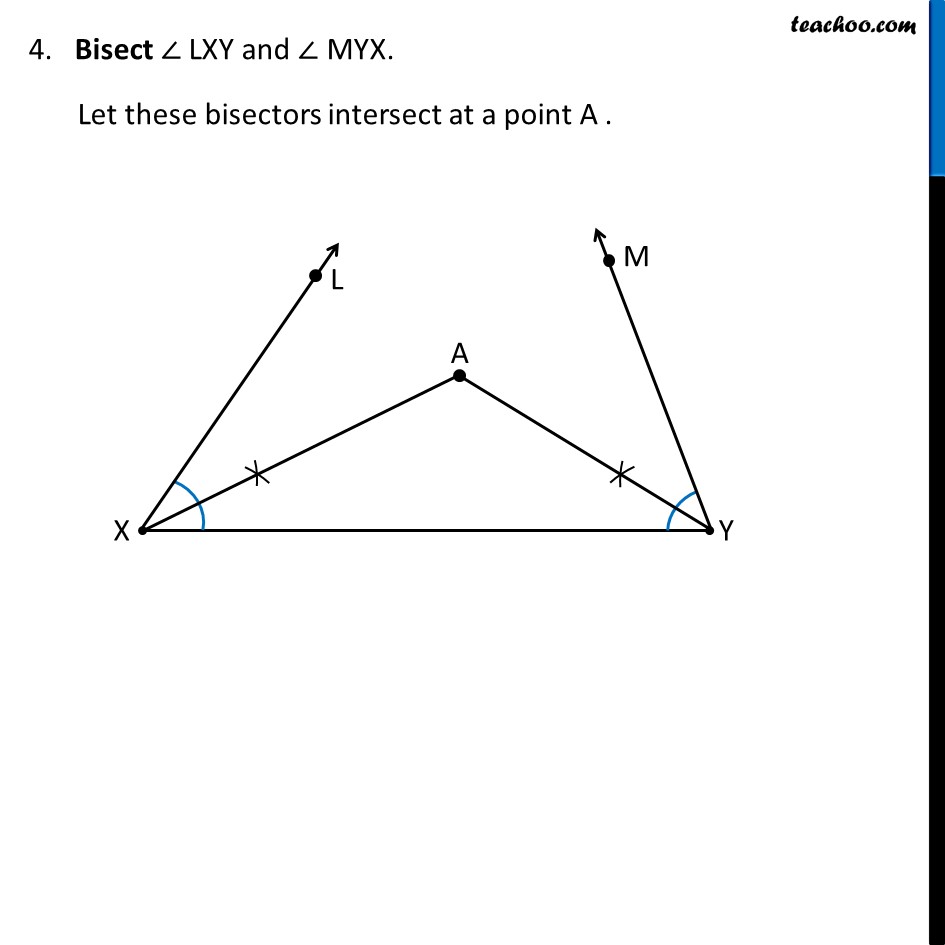
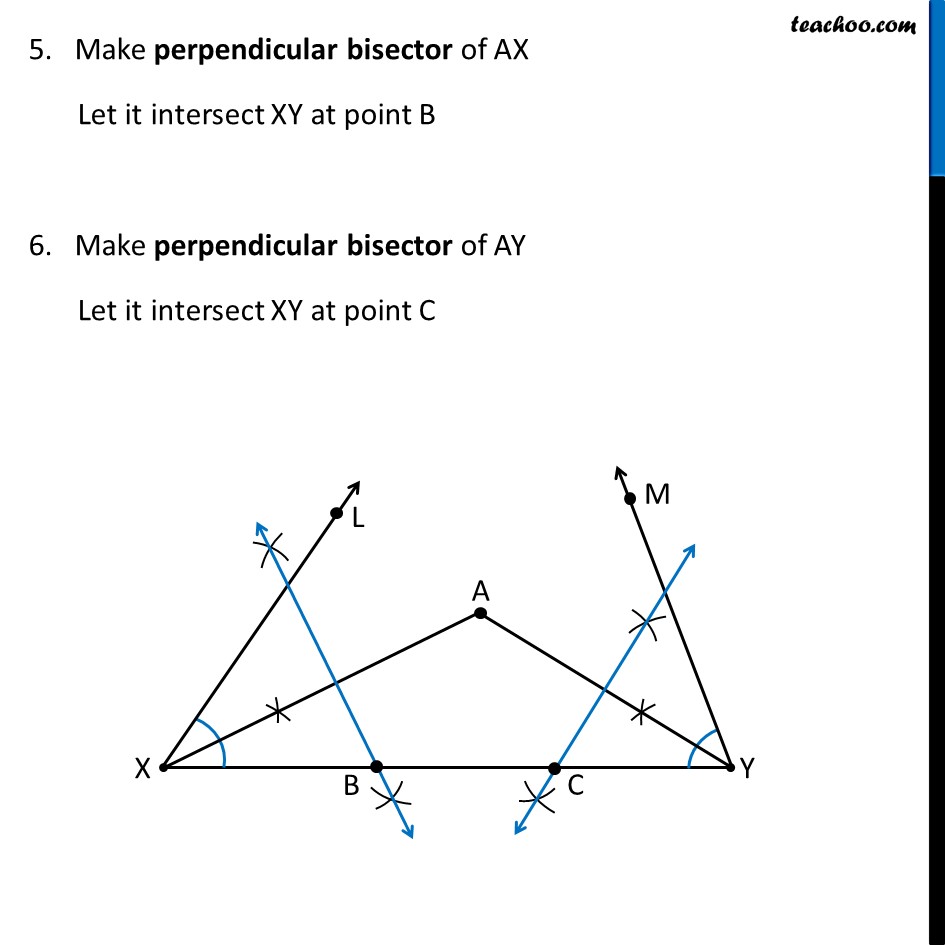
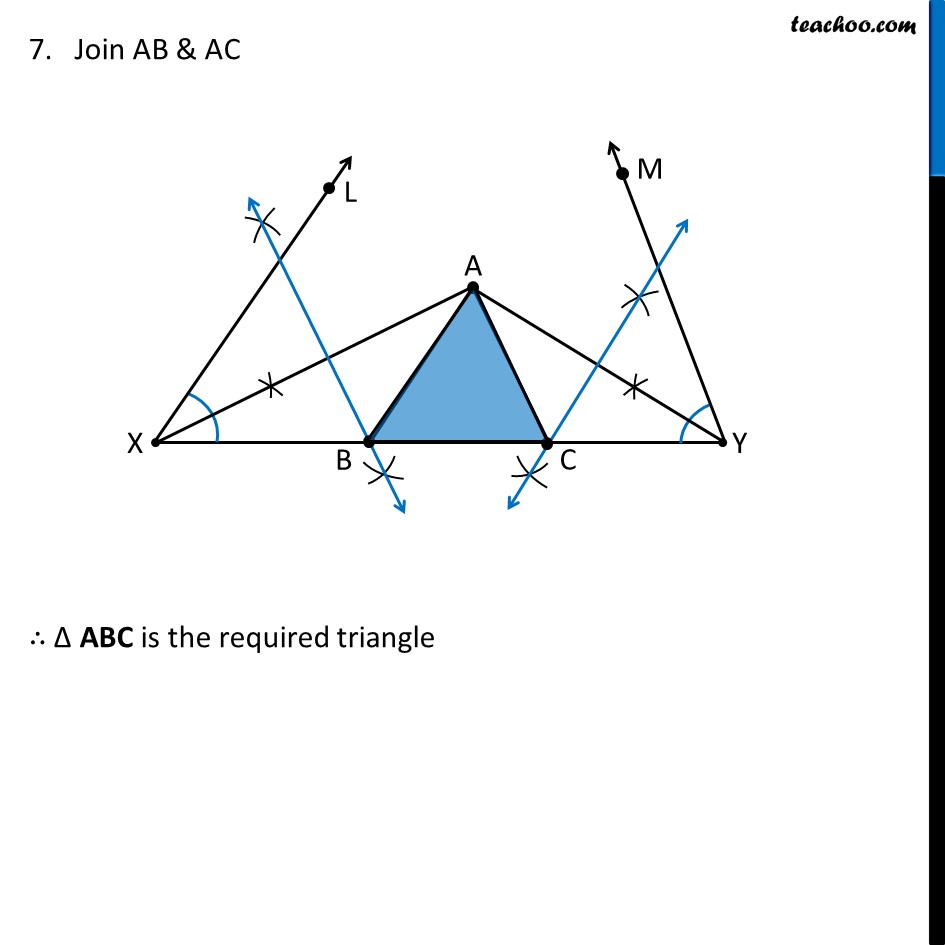
Construction 11.6 : To construct a triangle, given its perimeter and its two base angles. Given the base angles, ∠B and ∠C and AB + AC + BC, we have to construct ΔABC. Steps of Construction : Draw a line segment XY equal to AB + AC + BC. Make angle equal to ∠ B from point X Let the angle be ∠ LXY. Make angle equal to ∠ C from point Y Let the angle be ∠ MYX 4. Bisect ∠ LXY and ∠ MYX. Let these bisectors intersect at a point A . 5. Make perpendicular bisector of AX Let it intersect XY at point B 6. Make perpendicular bisector of AY Let it intersect XY at point C 7. Join AB & AC ∴ Δ ABC is the required triangle Justification To justify, we have to prove AB + BC + AC = XY ∠ LXY = ∠ B ∠ MYX = ∠ C Now,, Point B lies in perpendicular bisector of AX ∴ BX = BA Similarly, Point C lies in perpendicular bisector of AX ∴ CY = CA Steps of Construction : Draw a line segment, say XY equal to BC + CA + AB. Make angles LXY equal to ∠B and MYX equal to ∠C. Bisect ∠LXY and ∠MYX. Let these bisectors intersect at a point A . For proof of BX = BA, see Construction 11.4 For proof of CY = CA, see Construction 11.4 Now, we know that XY = XQ + BC + CY XY = AB + BC + AC So, XY = AB + BC + AC is proved, now let’s prove ∠ LXY = ∠ B & ∠ MYX = ∠ C (From (1) & (2)) In Δ AXB Since BX = BA ∴ ∠ BAX = ∠ AXB Now, ∠ ABC is the exterior angle of triangle AXB ∠ ABC = ∠ BAX + ∠ AXB ∠ ABC = ∠ AXB + ∠ AXB (Angles opposite to equal sides are equal) (Exterior angle is sum of interior opposite angles) ∠ ABC = 2 ∠ AXB ∠ ABC = ∠ LXY ∴ ∠ B = ∠ LXY Similarly, we can prove ∠ A = ∠ MYX Hence justified As AX is bisector of ∠ LXY, ∴ ∠ AXB = (∠ 𝐿𝑋𝑌)/2 2∠ AXB = ∠ LXY