Construction 11.4 - Constructions

Transcript

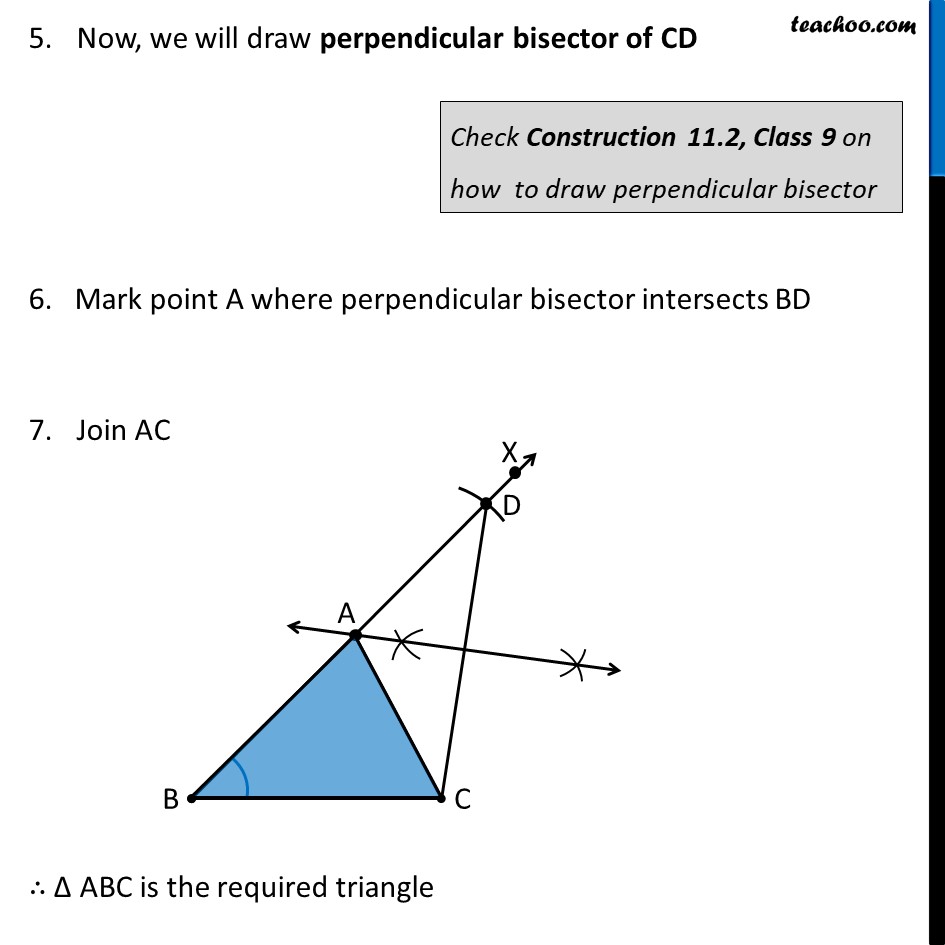
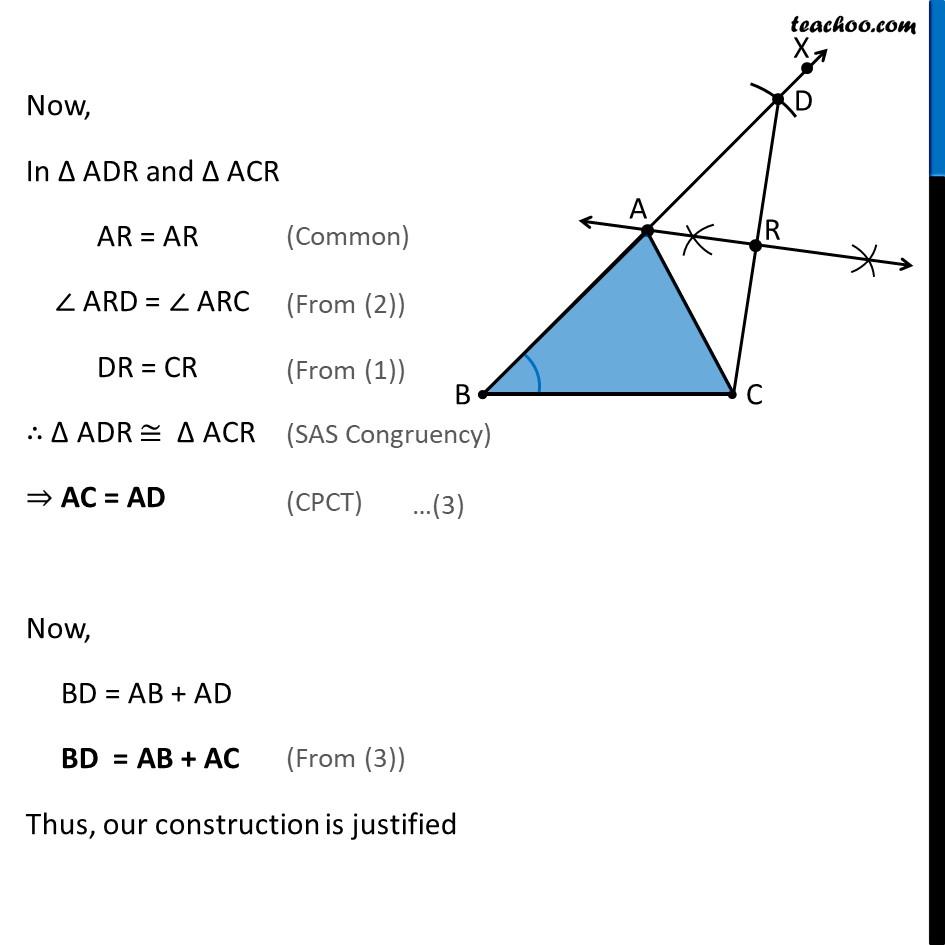
Construction 11.4 : To construct a triangle, given its base, a base angle and sum of other two sides. Given base BC, a base angle ∠B and the sum AB + AC, we need to construct Δ ABC Steps of Construction: Draw base BC 2. Now, let’s draw ∠ B Construct angle B from point B. Let the ray be BX 3. Open the compass to length AB + AC. From point B as center, cut an arc on ray BX. Let the arc intersect BX at D 4. Join CD Now, we will draw perpendicular bisector of CD 6. Mark point A where perpendicular bisector intersects BD Join AC ∴ Δ ABC is the required triangle Check Construction 11.2, Class 9 on how to draw perpendicular bisector Justification We need to prove that AB + AC = BD. Let perpendicular bisector intersect CD at point R Thus, AR is the perpendicular bisector of CD ∴ CR = DR & ∠ ARC = ∠ ARD = 90° Now, In Δ ADR and Δ ACR AR = AR ∠ ARD = ∠ ARC DR = CR ∴ Δ ADR ≅ Δ ACR ⇒ AC = AD Now, BD = AB + AD BD = AB + AC Thus, our construction is justified (Common) (From (2)) (From (1)) (SAS Congruency) (CPCT) (From (3))