
Constructing tangent from external point
Last updated at Dec. 16, 2024 by Teachoo




Transcript
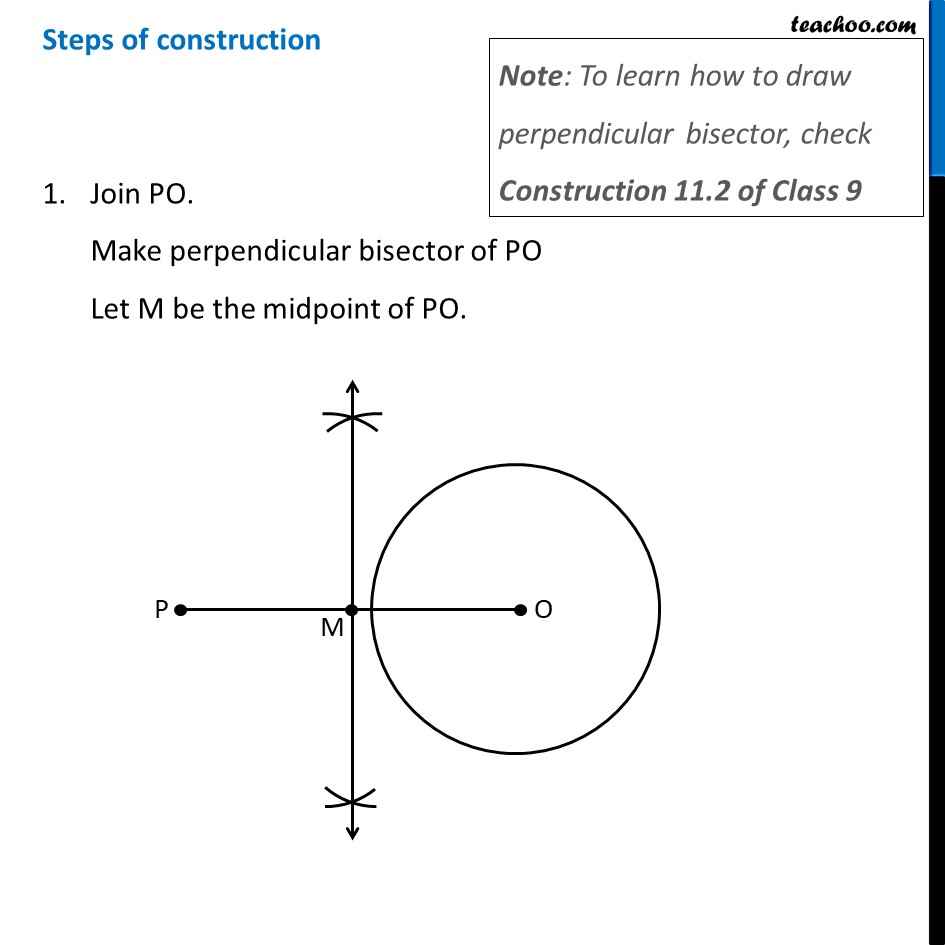
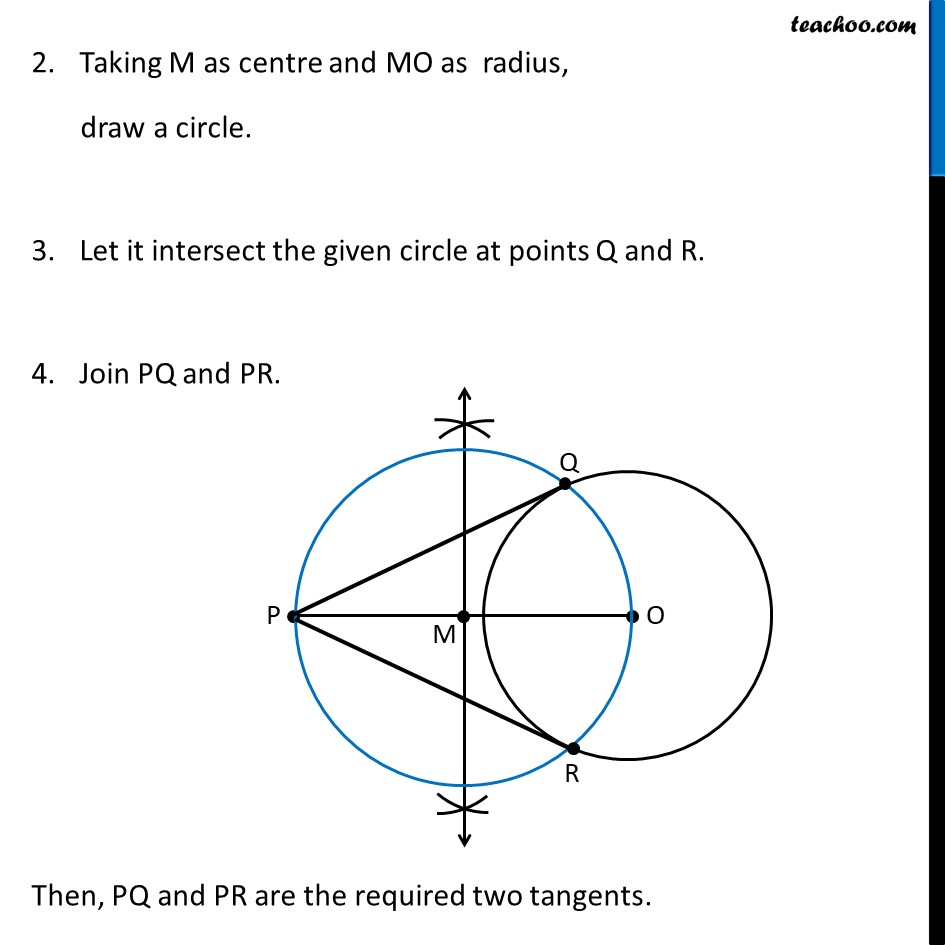
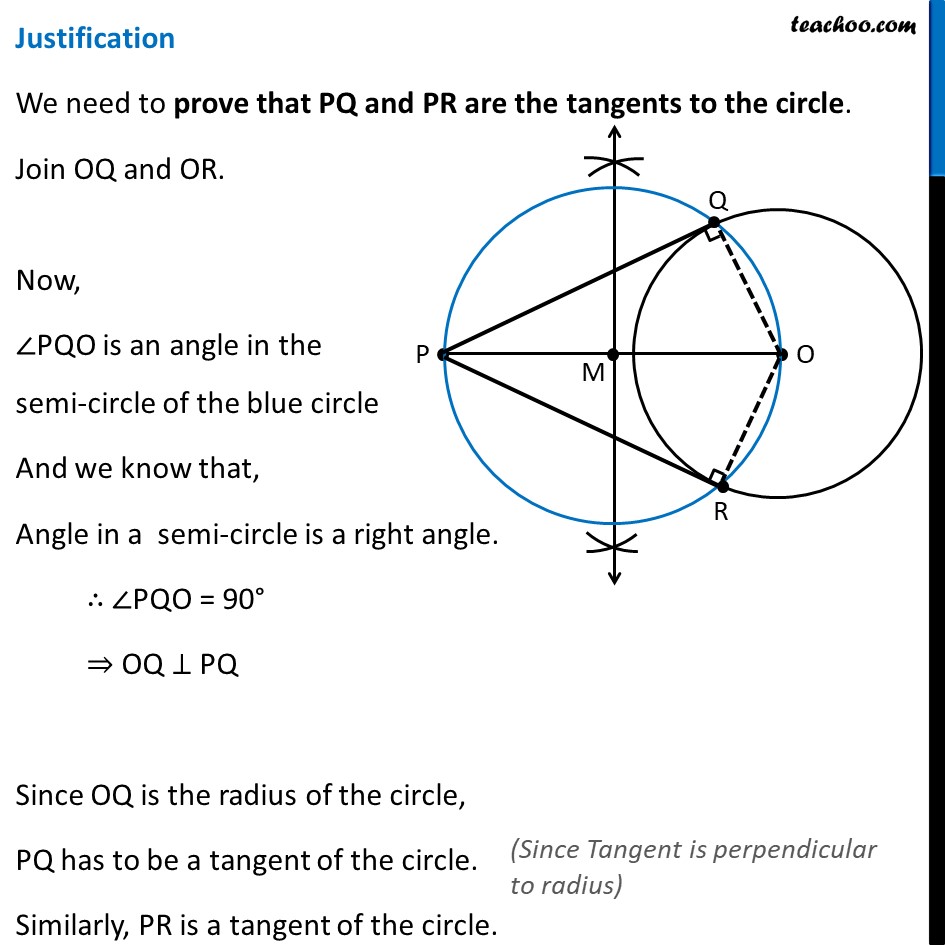
Construction 11.3 To construct the tangents to a circle from a point outside it. We are given a circle with center O and point P outside the circle We need to draw tangents from point P to the circle Let’s follow these steps Steps of construction Join PO. Make perpendicular bisector of PO Let M be the midpoint of PO. Taking M as centre and MO as radius, draw a circle. Let it intersect the given circle at points Q and R. Join PQ and PR. Then, PQ and PR are the required two tangents. Justification We need to prove that PQ and PR are the tangents to the circle. Join OQ and OR. Now, ∠PQO is an angle in the semi-circle of the blue circle And we know that, Angle in a semi-circle is a right angle. ∴ ∠PQO = 90° ⇒ OQ ⊥ PQ Since OQ is the radius of the circle, PQ has to be a tangent of the circle. Similarly, PR is a tangent of the circle.