Construction 11.1 - Constructions

Transcript

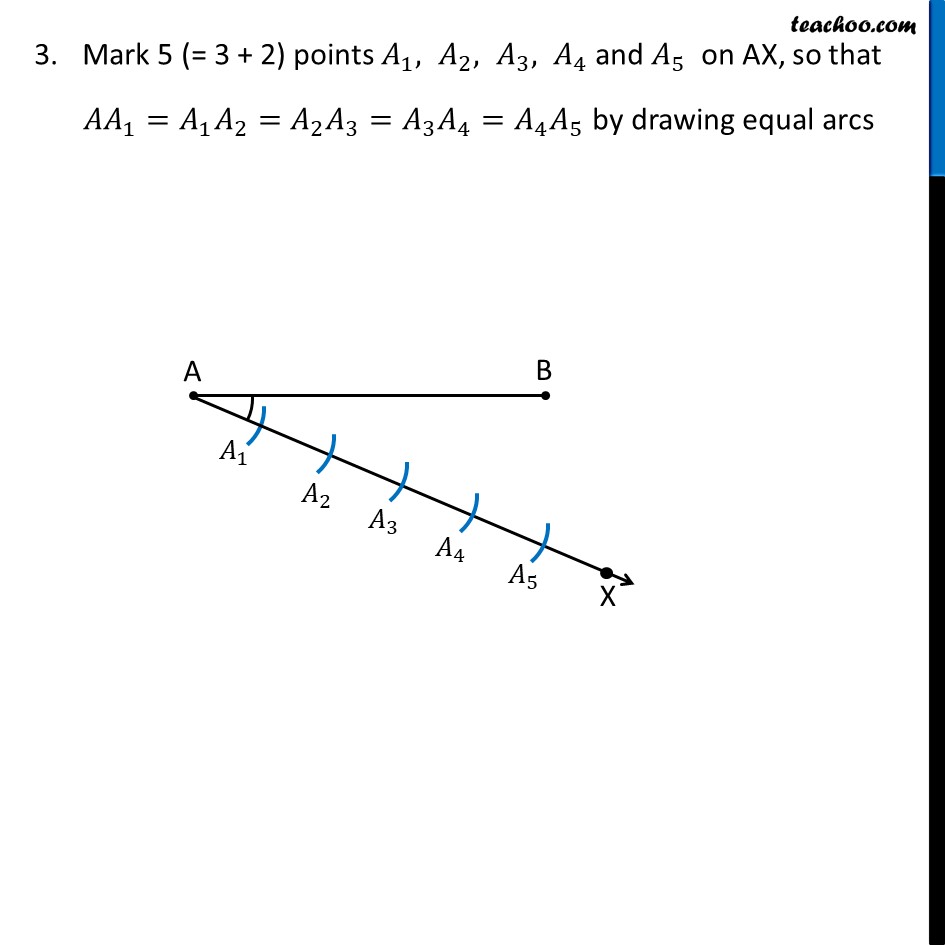
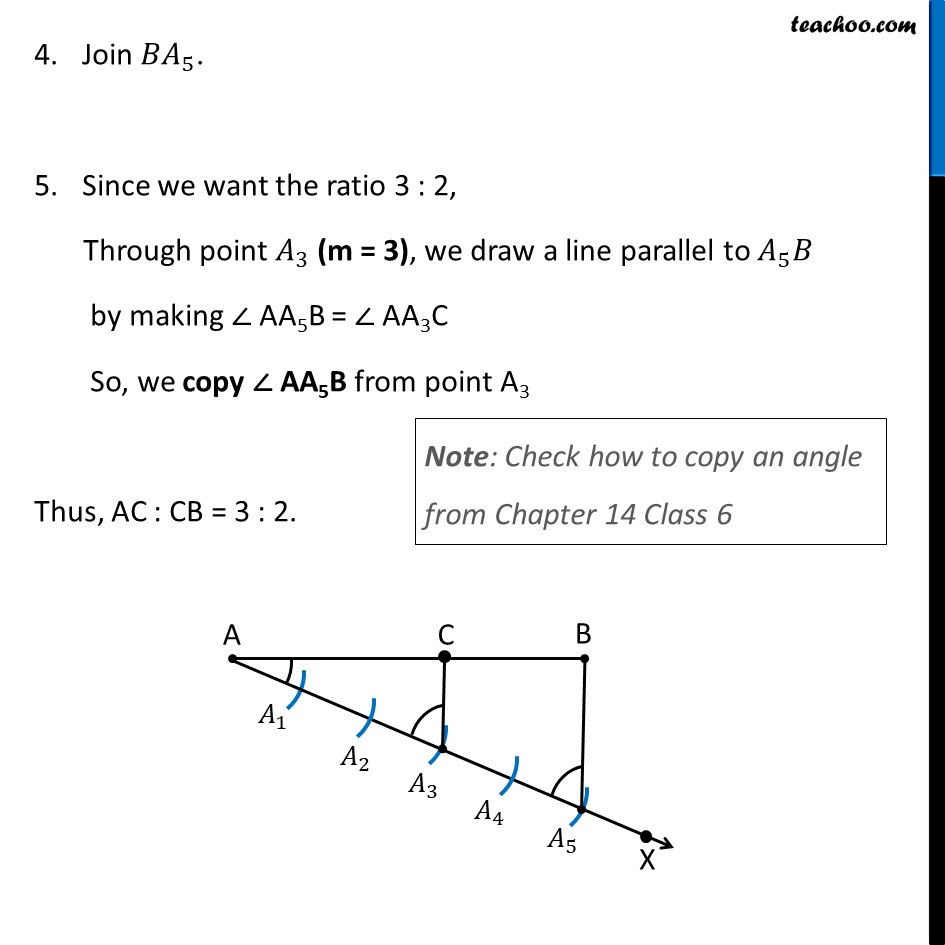
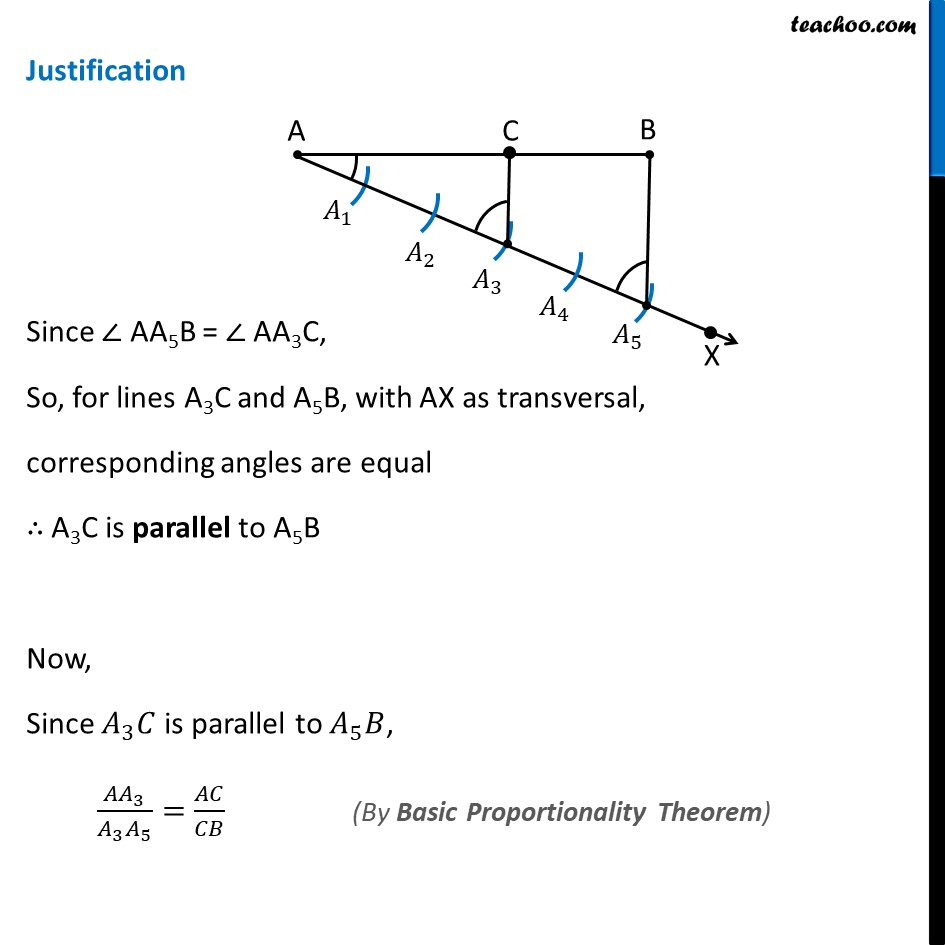
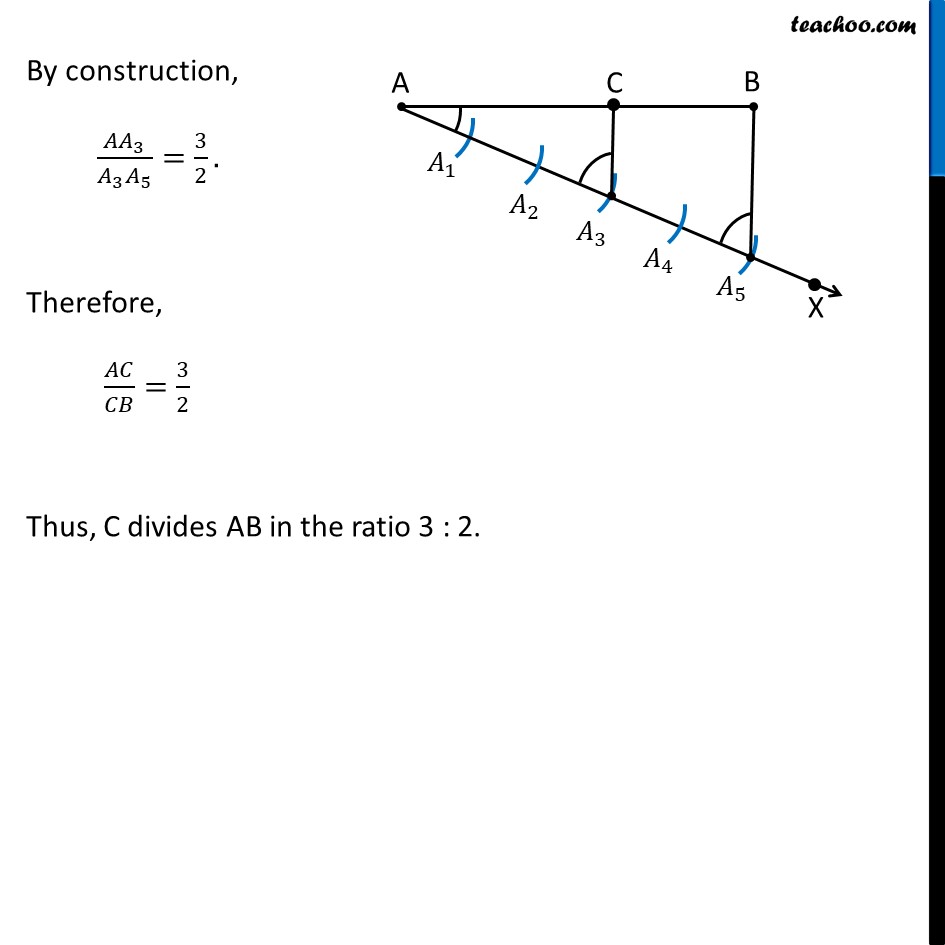
Construction 11.1 To divide a line segment in a given ratio. Let us divide a line segment AB into 3:2 ratio. Steps of construction: Draw line segment AB Draw any ray AX, making an acute angle (angle less than 90°) with AB. Mark 5 (= 3 + 2) points 𝐴_1, 𝐴_2, 𝐴_3, 𝐴_4 and 𝐴_5 on AX, so that 〖𝐴𝐴〗_1=〖𝐴_1 𝐴〗_2=〖𝐴_2 𝐴〗_3=〖𝐴_3 𝐴〗_4=〖𝐴_4 𝐴〗_5 by drawing equal arcs Join 〖𝐵𝐴〗_5. Since we want the ratio 3 : 2, Through point 𝐴_3 (m = 3), we draw a line parallel to 𝐴_5 𝐵 by making ∠ AA5B = ∠ AA3C So, we copy ∠ AA5B from point A3 Thus, AC : CB = 3 : 2. Justification Since ∠ AA5B = ∠ AA3C, So, for lines A3C and A5B, with AX as transversal, corresponding angles are equal ∴ A3C is parallel to A5B Now, Since 𝐴_3 𝐶 is parallel to 𝐴_5 𝐵, 〖𝐴𝐴〗_3/(𝐴_3 𝐴_5 )=𝐴𝐶/𝐶𝐵 By construction, 〖𝐴𝐴〗_3/(𝐴_3 𝐴_5 )=3/2. Therefore, 𝐴𝐶/𝐶𝐵=3/2 Thus, C divides AB in the ratio 3 : 2.