Question 1 - Diet problems - Chapter 12 Class 12 Linear Programming

Transcript

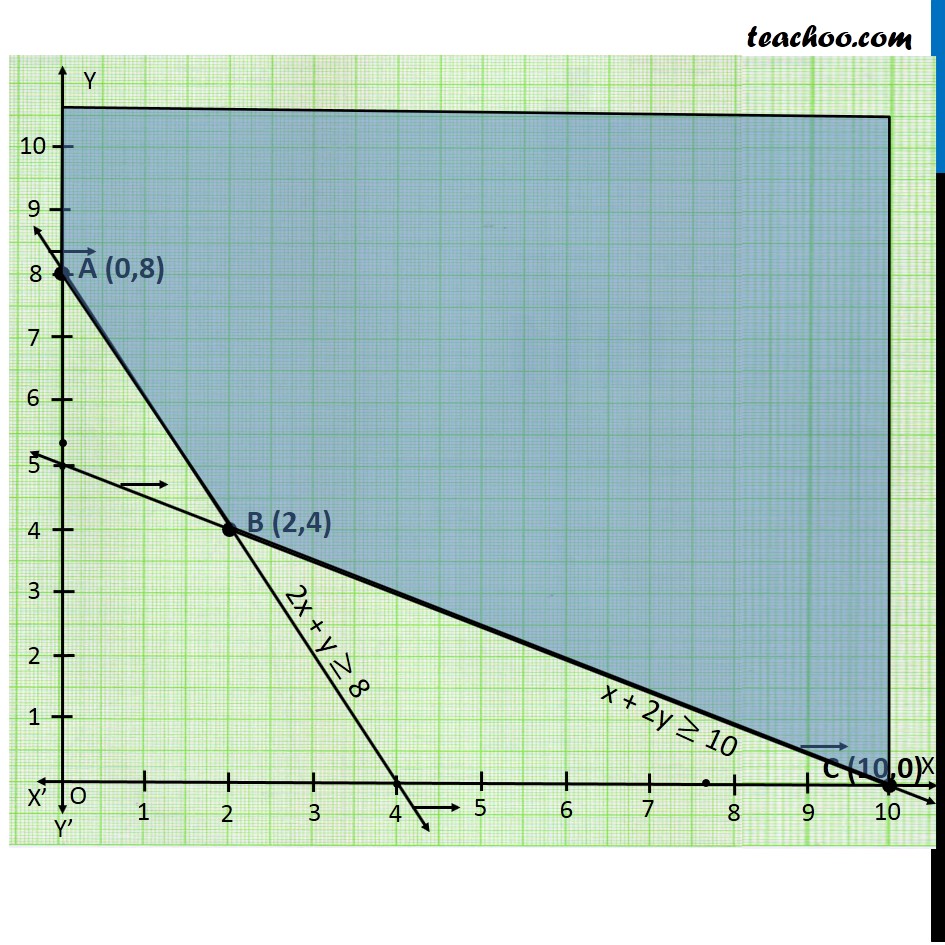
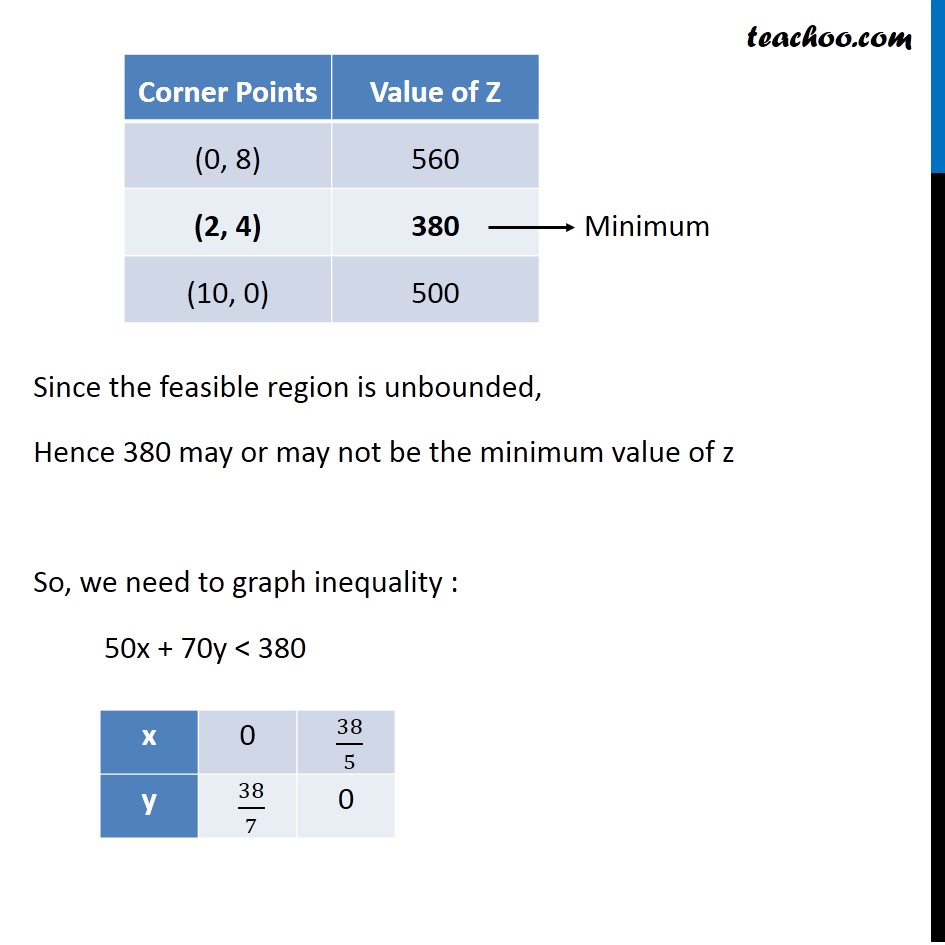
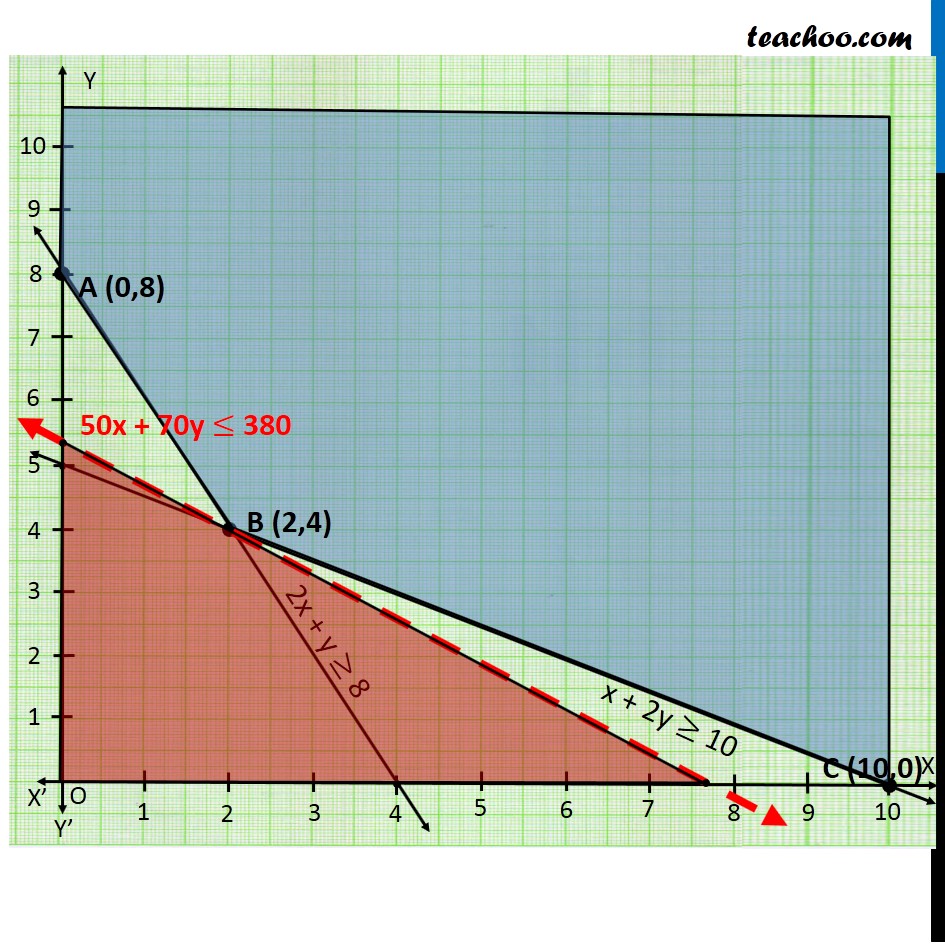
Question 1 (Diet problem): A dietician wishes to mix two types of foods in such away that vitamin contents of the mixture contain atleast 8 units of vitamin A and 10 units of vitamin C. Food ‘I’ contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C. Food ‘II’ contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs Rs 50 per kg to purchase Food ‘I’ and Rs 70 per kg to purchase Food ‘II’. Formulate this problem as a linear programming problem to minimise the cost of such a mixture. Let the mixture contain x kg of food I and y kg of food II According to Question : As, we need to minimize the cost of mixture, we will use function minimize Z. Vitamin A Food I contains → 2 units Food II contains → 1 units Total Requirement → atleast 8 units ∴ 2x + y ≥ 8 Vitamin C Food I contains → 1 units Food II contains → 2 units Total Requirement → atleast 10 units ∴ x + 2y ≥ 10 Cost of Food 1 Per Kg = Rs 50 Cost of Food 2 Per kg = Rs 70 ∴ Z = 50 x + 70 y (3) Hence, Combining the constraints : Minimize Z = 50x + 70y Subject to constraints : 2x + y ≥ 8 x + 2y ≥ 10 x, y ≥ 0 Since the feasible region is unbounded, Hence 380 may or may not be the minimum value of z So, we need to graph inequality : 50x + 70y < 380 As, there is no common points between the feasible region inequality. ∴ 380 is the minimum value of z Hence the Optimal mixing strategy would be to mix 2 kg of Food I & 4 kg of Food II , So minimum cost is Rs 380.