Example 4 - Chapter 12 Class 12 Linear Programming

Last updated at April 16, 2024 by

Example 4 - Determine graphically minimum Z = -50x + 20y

Example 4 - Chapter 12 Class 12 Linear Programming - Part 2
Example 4 - Chapter 12 Class 12 Linear Programming - Part 3
Example 4 - Chapter 12 Class 12 Linear Programming - Part 4
Example 4 - Chapter 12 Class 12 Linear Programming - Part 5

Transcript

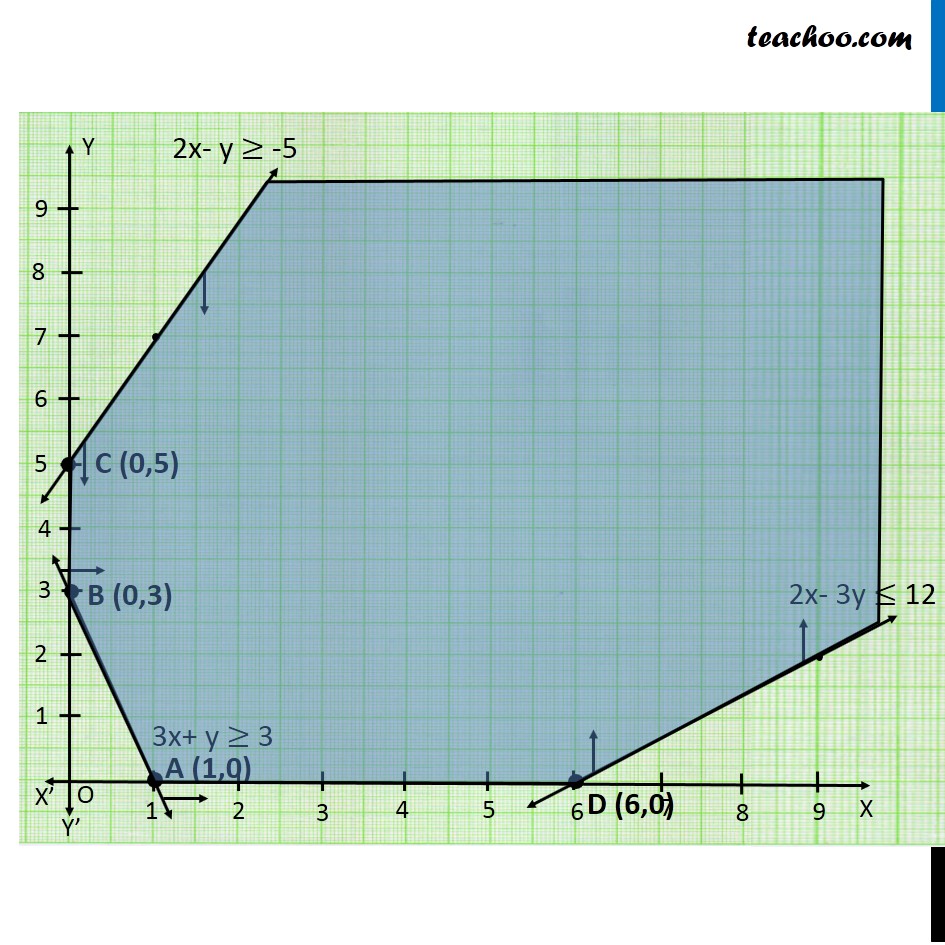
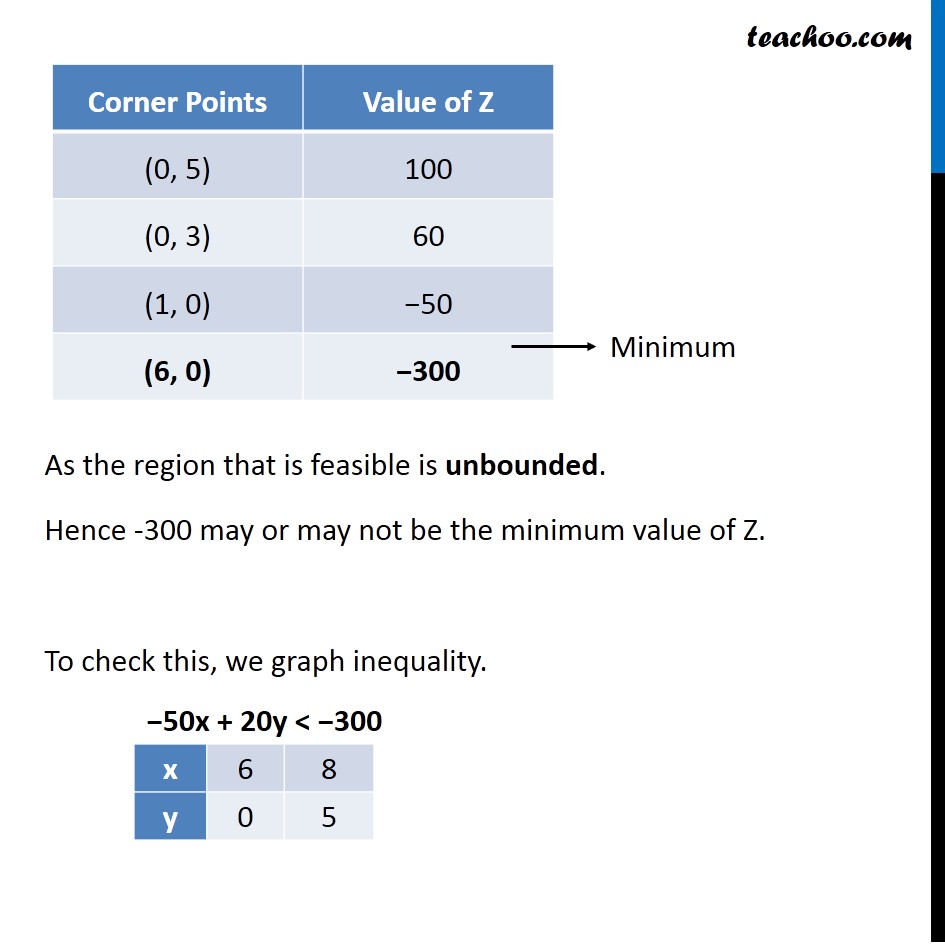
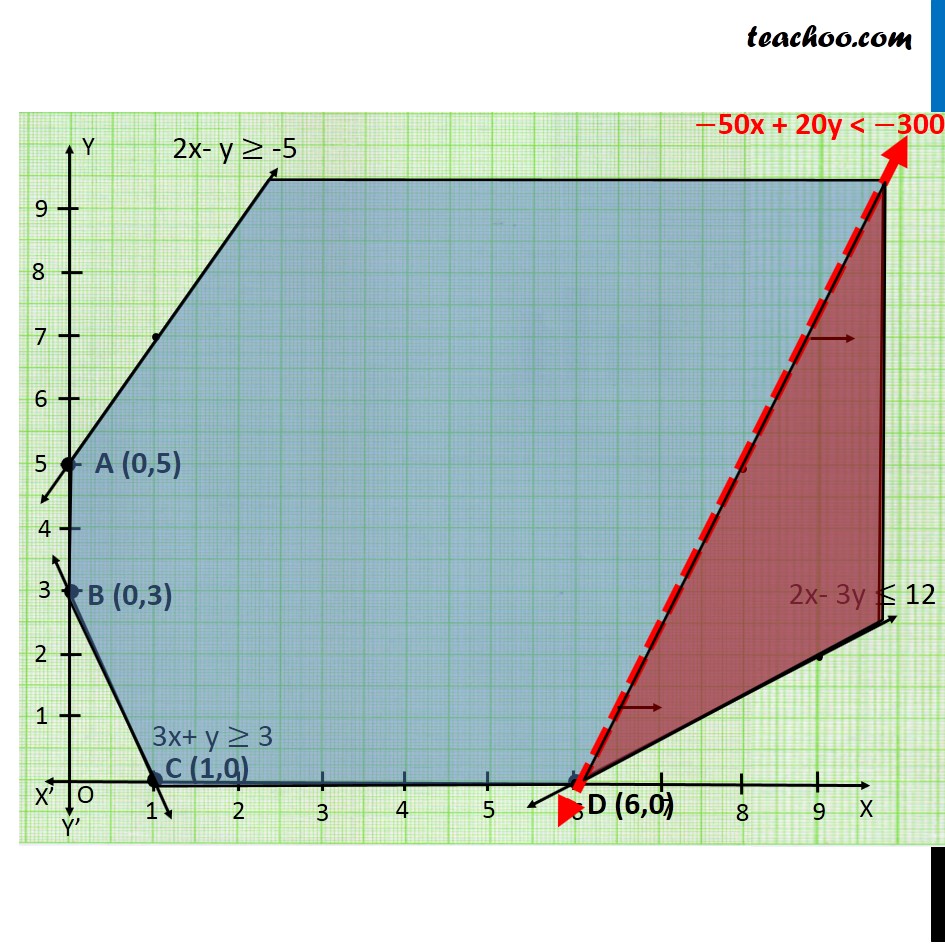
Example 4 Determine graphically the minimum value of the objective function Z = – 50x + 20y. Subject to the constraints: 2x – y ≥ – 5 3x + y ≥ 3 2x – 3y ≤ 12 x ≥ 0, y ≥ 0 Minimum Z = −50x + 20y Subject to, 2x – y ≥ – 5 3x + y ≥ 3 2x – 3y ≤ 12 x ≥ 0, y ≥ 0 As the region that is feasible is unbounded. Hence -300 may or may not be the minimum value of Z. To check this, we graph inequality. As, there are some common points between the feasible region & the inequality. Hence, 300 is not the minimum value of Z. ∴ Z has no minimum value

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.