Question 1 - Diet problems - Chapter 12 Class 12 Linear Programming

Transcript

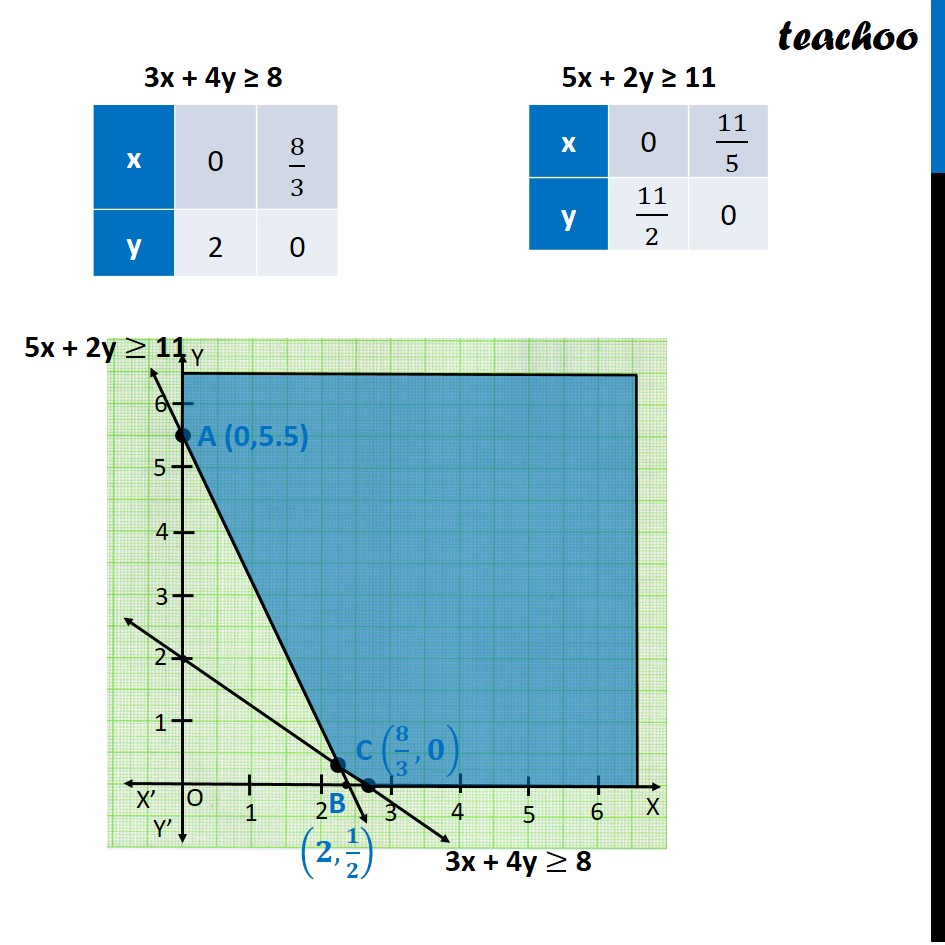
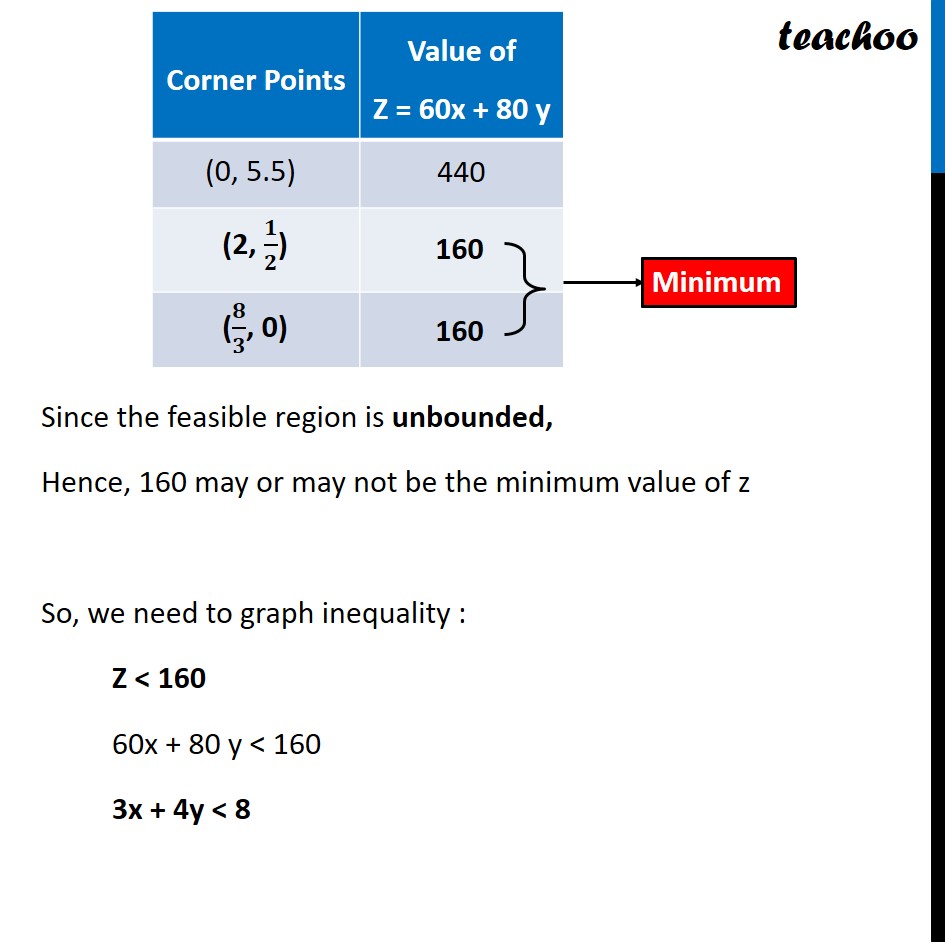
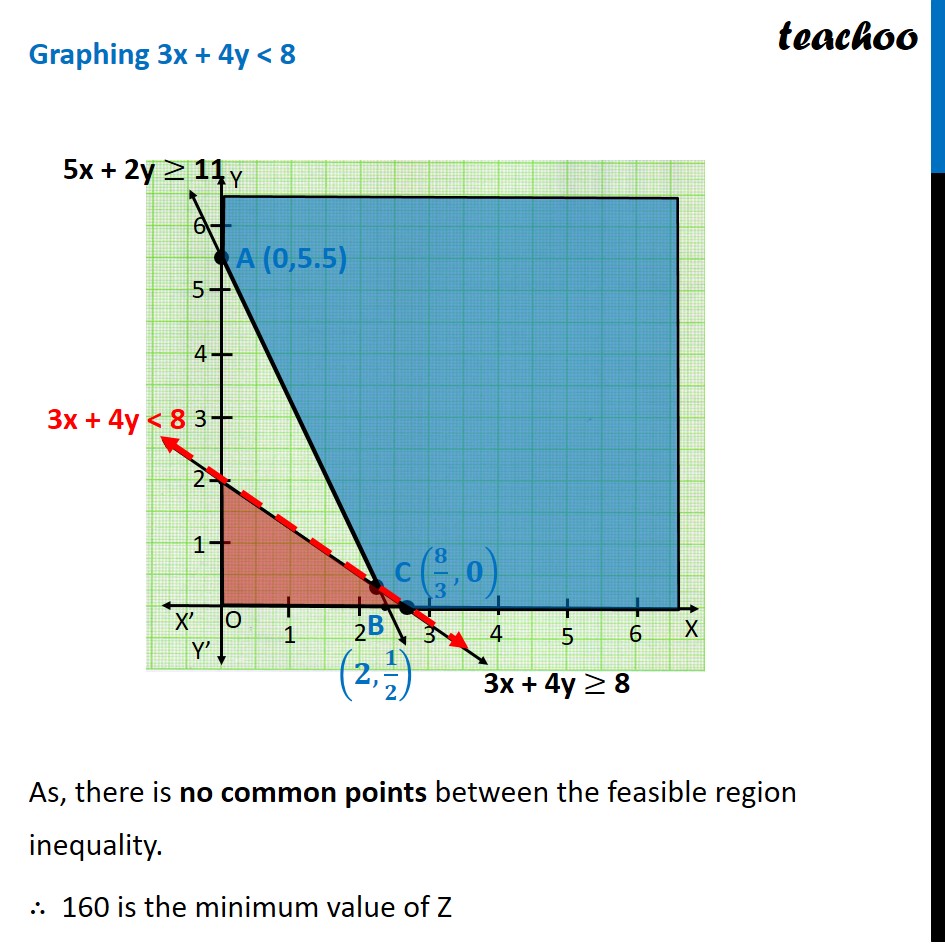
Question 1 Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food P costs Rs 60/kg and Food Q costs Rs 80/kg. Food P contains 3 units/kg of Vitamin A and 5 units / kg of Vitamin B while food Q contains 4 units/kg of Vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.Let the mixture contain x kg of food P & y kg of food Q According to Question Also, we need to minimize cost of mixture, Cost of Food P per kg = Rs 60 Cost of Food Q per kg = Rs 80 Vitamin A Food P contains → 3 units Food Q contains → 4 units Total Requirement → Atleast 8 units ∴ 3x + 4y ≥ 8 Vitamin B Food P contains → 5 units Food Q contains → 2 units Total Requirement → Atleast 11 units ∴ 5x + 2y ≥ 11 ∴ Cost of Mixture: Z = 60x + 80 y Hence, Combining the constraints : Minimize Z = 60x + 80 y Subject to constraints 3x + 4y ≥ 8 5x + 2y ≥ 11 x ≥ 0, y ≥ 0 Since the feasible region is unbounded, Hence, 160 may or may not be the minimum value of z So, we need to graph inequality : Z < 160 60x + 80 y < 160 3x + 4y < 8 Graphing 3x + 4y < 8 As, there is no common points between the feasible region inequality. ∴ 160 is the minimum value of Z Since, Z is minimum at two points (8/3 ", 0" ) & (2, 1/2) Hence, Minimum cost of mixture is Rs 160 and at all points joining (𝟖/𝟑 ", 0" ) & (𝟐,𝟏/𝟐)