You are here
Ex 12.1, 9 - Chapter 12 Class 12 Linear Programming
Last updated at August 19, 2026 by Teachoo
Linear equations given - Unbounded
Chapter 12 Class 12 Linear Programming
Concept wise
- Linear equations given - Bounded
- Linear equations given - Not feasible
-
Linear equations given - Unbounded
- Diet problems
- Manufacturing problems
- Other questions
- Transport problems
Transcript
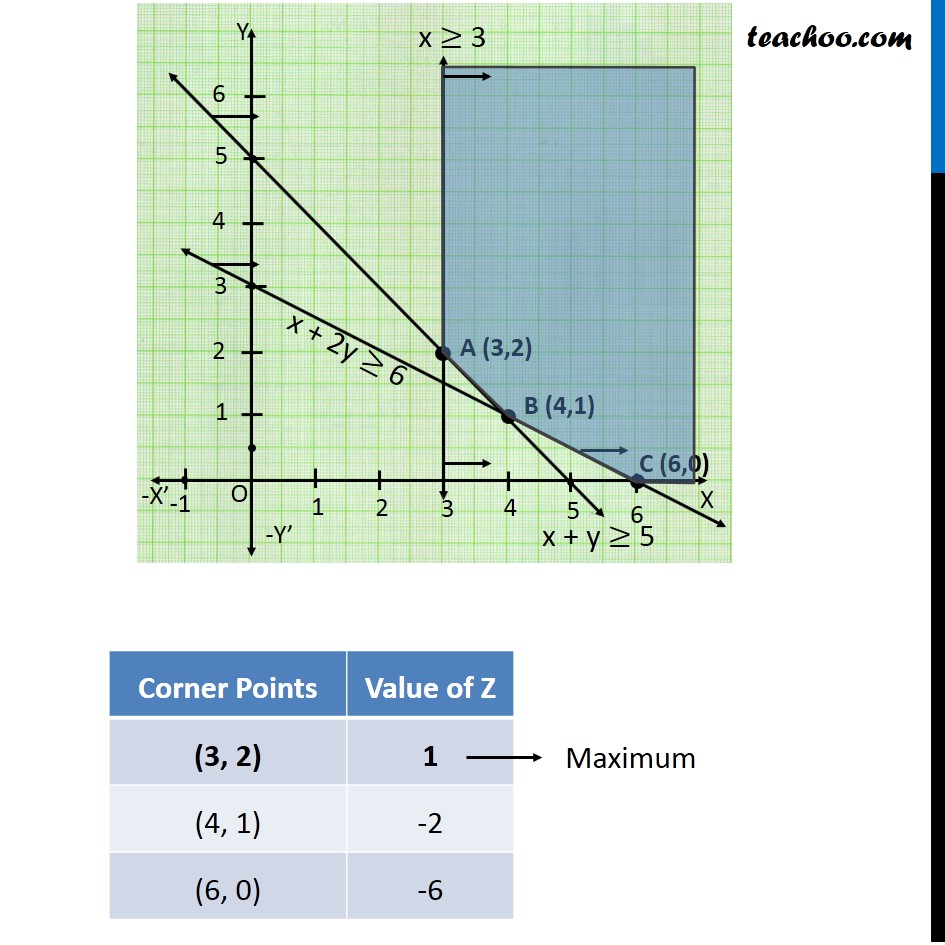
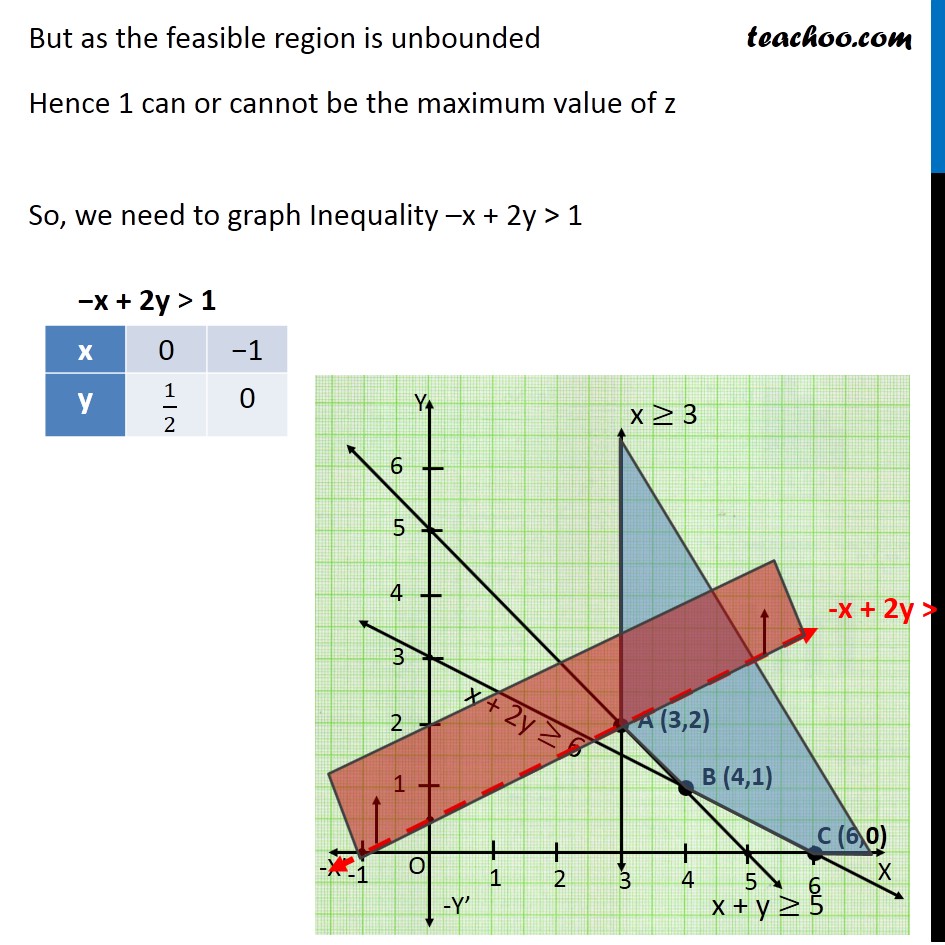
Ex 12.1, 9 Maximise Z = – x + 2y, subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0 Maximize Z = –x + 2y Subject to, x ≥ 3 x + y ≥ 5 x + 2y ≥ 6 y ≥ 0 But as the feasible region is unbounded Hence 1 can or cannot be the maximum value of z So, we need to graph Inequality –x + 2y > 1 Since feasible region of –x + 2y > 1 has some points in common. So there is no maximum value for Z subject to given constraints.
