Misc 3 - Chapter 12 Class 12 Linear Programming (Important Question)

Transcript

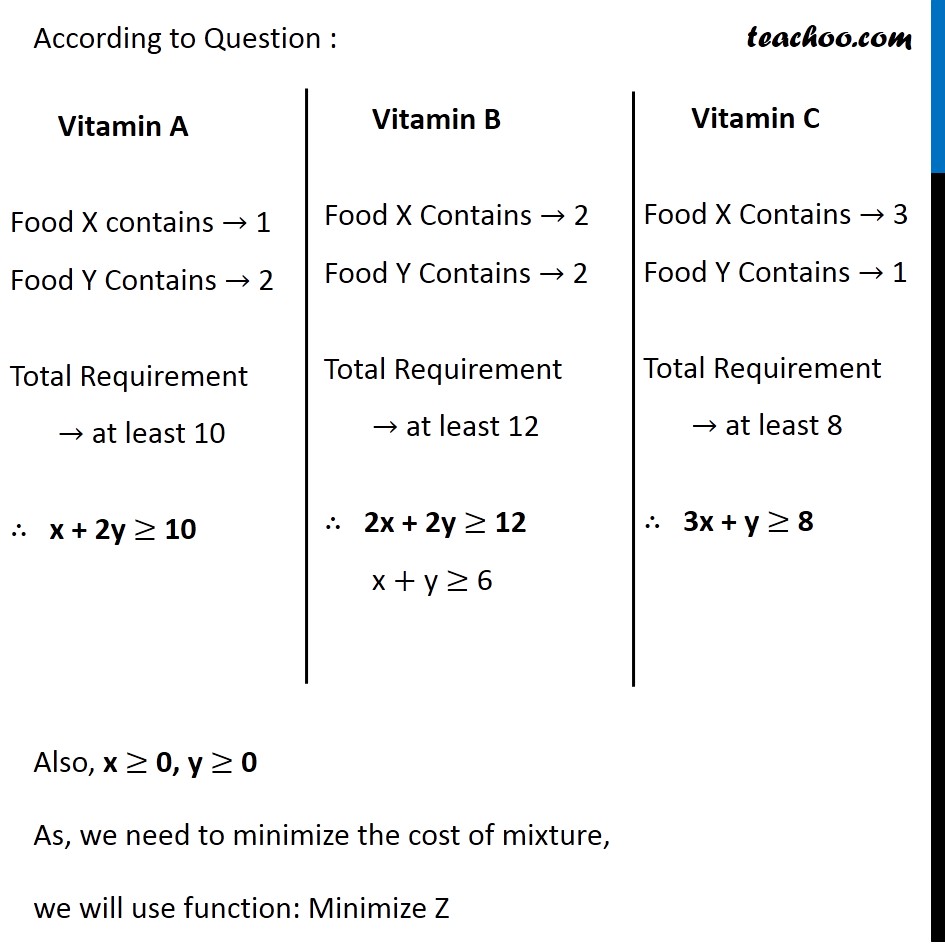
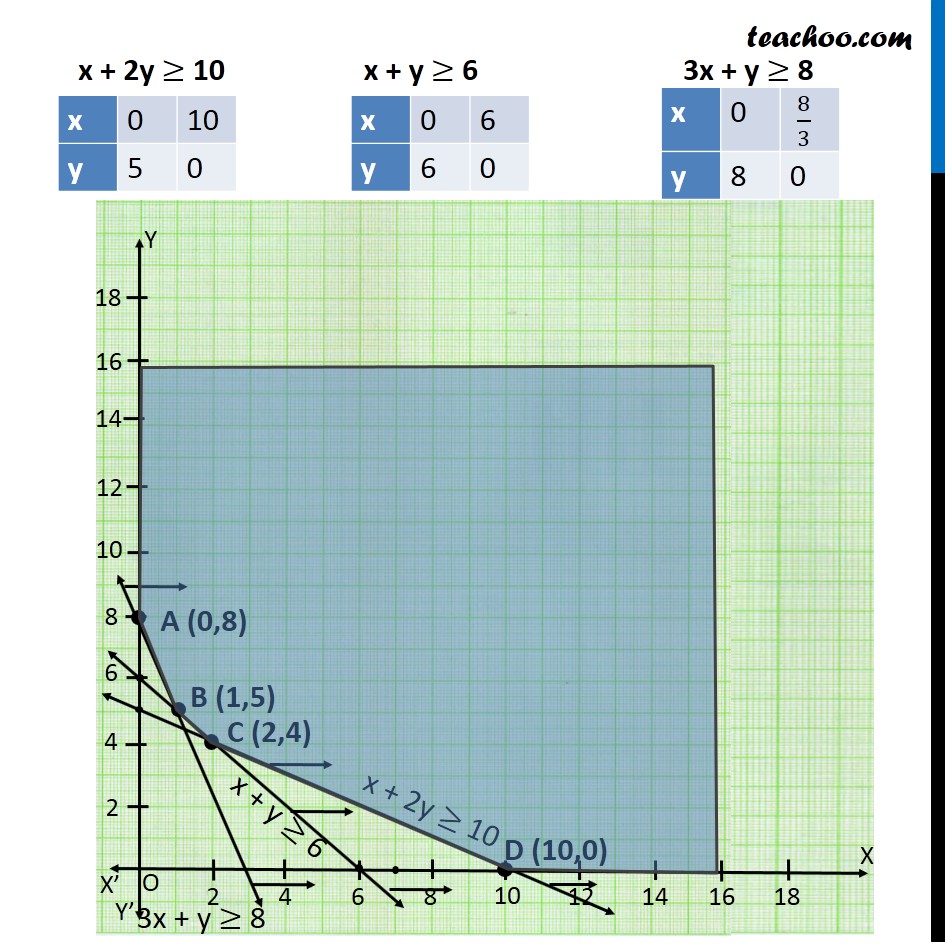
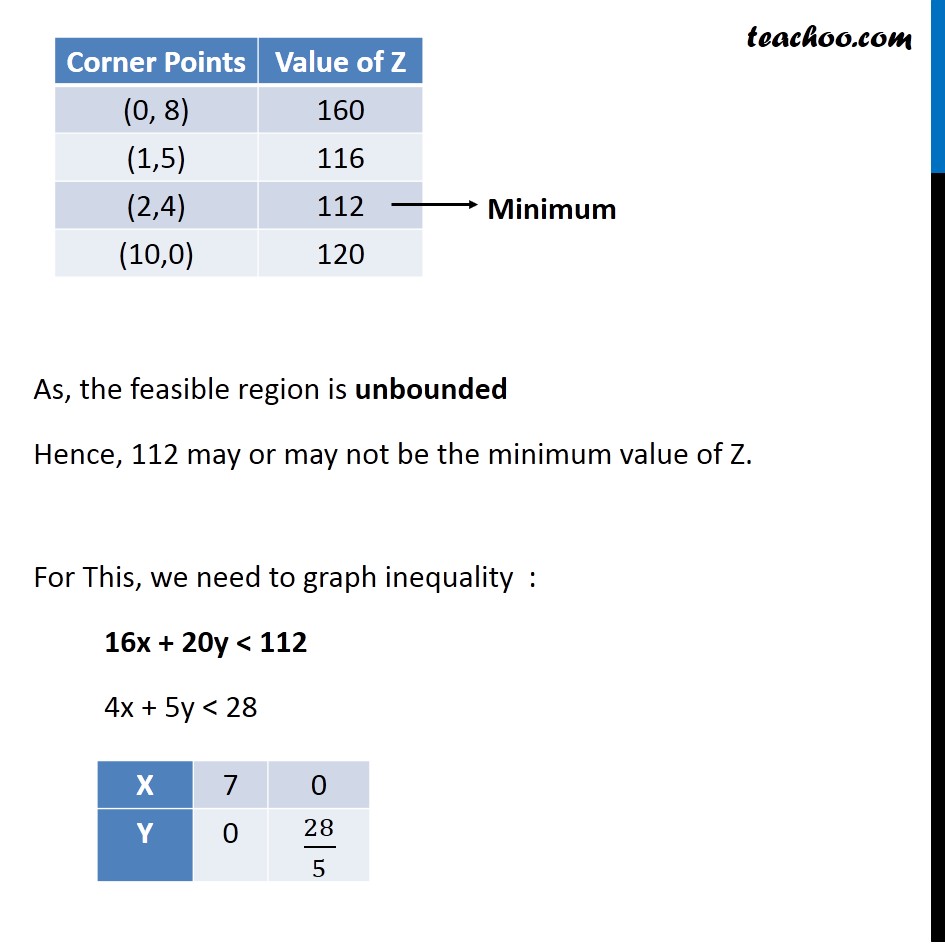
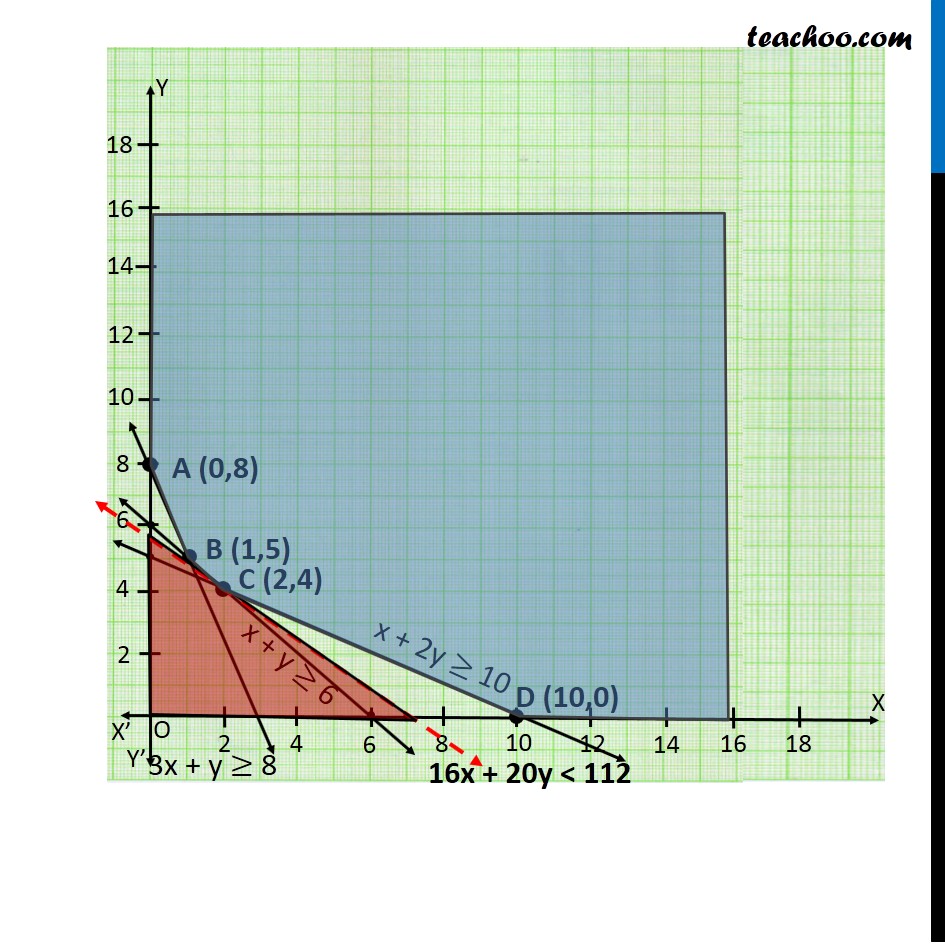
Misc 3 A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below: One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet? Let the mixture Contains x units of Food x The mixture Contains y units of Food y Let the mixture Contains x units of Food x The mixture Contains y units of Food y Vitamin A Food X contains → 1 Food Y Contains → 2 Total Requirement → at least 10 ∴ x + 2y ≥ 10 Vitamin B Food X Contains → 2 Food Y Contains → 2 Total Requirement → at least 12 ∴ 2x + 2y ≥ 12 x + y ≥ 6 Vitamin C Food X Contains → 3 Food Y Contains → 1 Total Requirement → at least 8 ∴ 3x + y ≥ 8 Now, Food X cost → Rs 16 Food Y Cost → Rs 20 ∴ Z = 16x + 20Y Combining all Constraints : Min Z = 16x + 20y Subject to Constraints, x + 2y ≥ 10 x + y ≥ 6 3x + y ≥ 8 x ≥ 0, y ≥ 0 As, the feasible region is unbounded Hence, 112 may or may not be the minimum value of Z. For This, we need to graph inequality : 16x + 20y < 112 4x + 5y < 28 Since, there is no point in Common Between the feasible region & inequality. Hence, minimum value of Z is 112. Thus, Cost of Mixture will be minimum if 2 packets of Food X & 4 Packets of Food Y are used. Minimum cost of mixture is Rs 112.