

Standard deviation and variance - Continuous frequency (grouped data)
Standard deviation and variance - Continuous frequency (grouped data)
Last updated at December 16, 2024 by Teachoo



Transcript
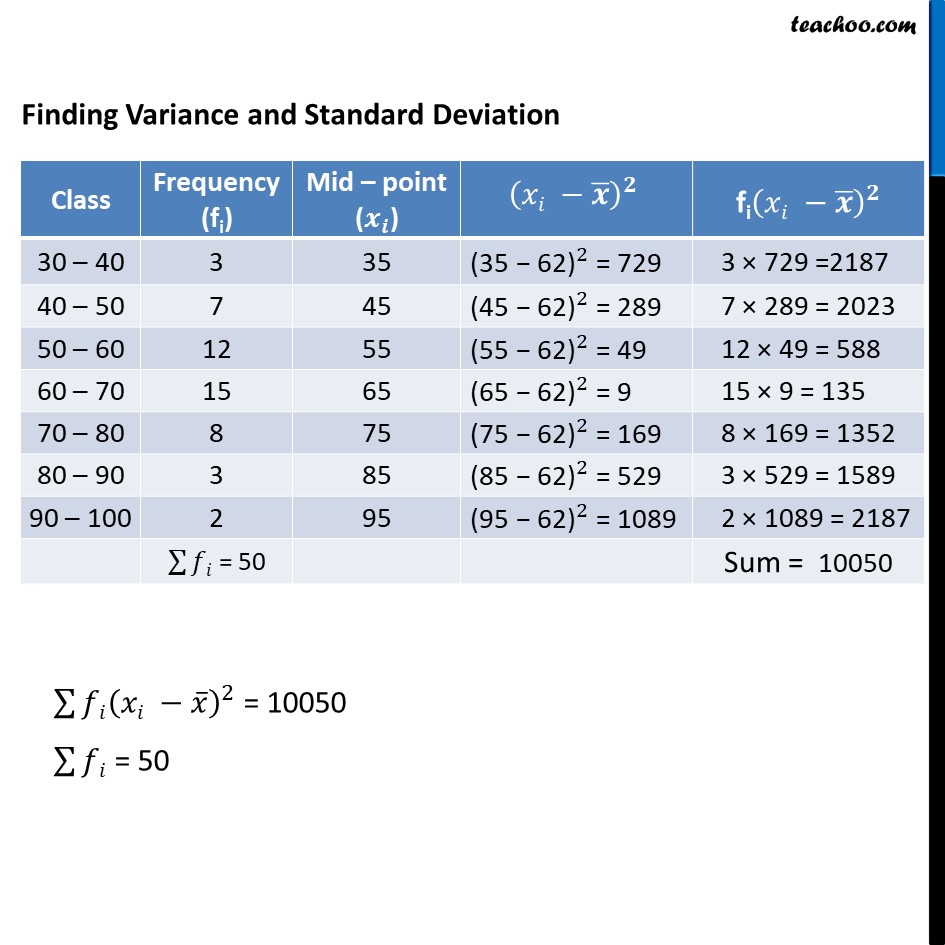
Example 10 - Chapter 15 Class 11 Statistics - NCERT Calculate the mean, variance and standard deviation for the following distribution : Finding Variance and Standard Deviation Class Frequency (fi) Mid – point (x_i) fixi 30 – 40 3 35 35 × 3 = 105 40 – 50 7 45 45 × 7 = 315 50 – 60 12 55 55 × 12 = 660 60 – 70 15 65 65 × 15 = 975 70 – 80 8 75 75 × 8 = 600 80 – 90 3 85 85 × 3 = 255 90 – 100 2 95 95 × 2 = 190 ∑▒fi = 50 ∑▒fixi = 3100 ∑▒𝑓𝑖𝑥𝑖 = 3100 ∑▒𝑓𝑖 = 50 Mean (𝒙 ̅) = (∑▒𝑓𝑖𝑥𝑖)/(∑▒𝑓𝑖) = 3100/50 = 62 Finding Variance and Standard Deviation Class Frequency (fi) Mid – point (x_i) (xi -x ̅ )^2 fi(xi -x ̅ )^2 30 – 40 3 35 〖"(35 - 62)" 〗^2 = 729 3 × 729 =2187 40 – 50 7 45 〖"(45 - 62)" 〗^2 = 289 7 × 289 = 2023 50 – 60 12 55 〖"(55 - 62)" 〗^2 = 49 12 × 49 = 588 60 – 70 15 65 〖"(65 - 62)" 〗^2 = 9 15 × 9 = 135 70 – 80 8 75 〖"(75 - 62)" 〗^2 = 169 8 × 169 = 1352 80 – 90 3 85 〖"(85 - 62)" 〗^2 = 529 3 × 529 = 1589 90 – 100 2 95 〖"(95 - 62)" 〗^2 = 1089 2 × 1089 = 2187 ∑▒fi = 50 Sum = 10050 ∑▒〖𝑓𝑖(𝑥𝑖 −𝑥 ̅ )^2 〗 = 10050 ∑▒𝑓𝑖 = 50 Variance ("σ" ^2) = 1/𝑁 ∑▒〖𝑓𝑖(𝑥𝑖 −𝑥 ̅ )^2 〗 = 1/50 ×10050 = 201 Standard deviation (σ) = √("201" ) (σ) = 14.17