Question 6 - Definite Integral as a limit of a sum - Chapter 7 Class 12 Integrals

Transcript

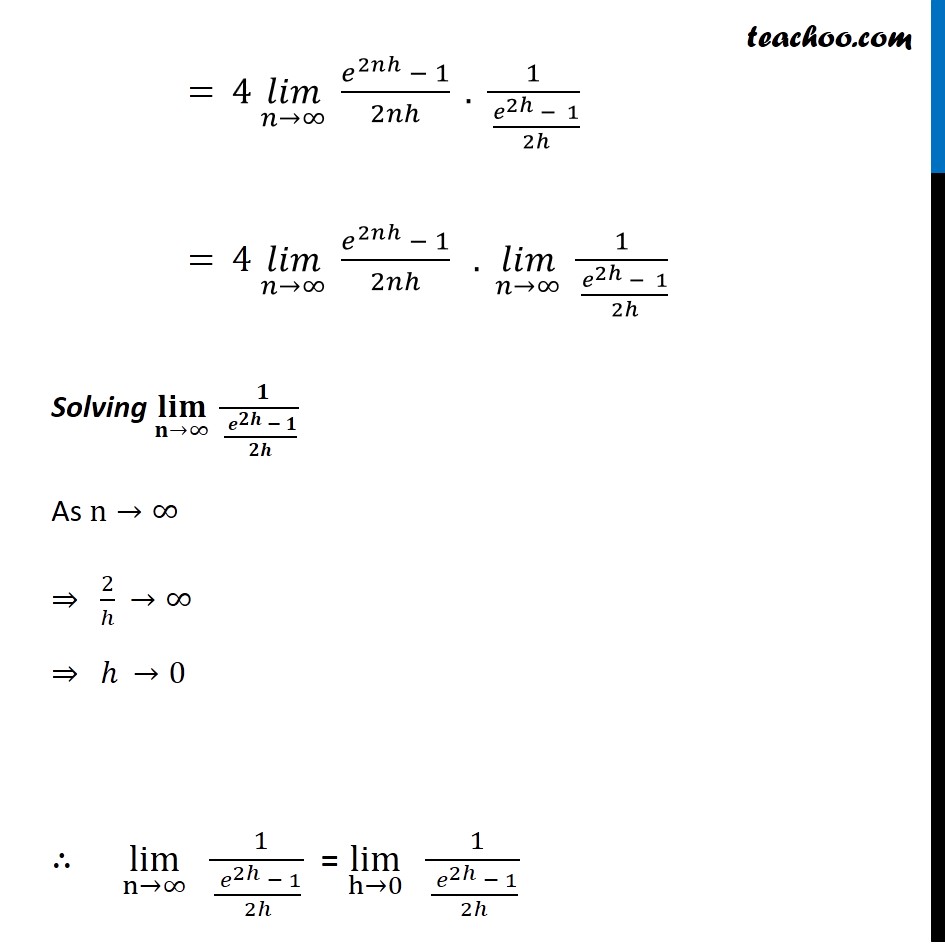
Question 6 ∫1_0^4▒(𝑥+𝑒2𝑥)𝑑𝑥 Let I = ∫1_0^4▒(𝑥+𝑒2𝑥)𝑑𝑥 I = ∫1_0^4▒〖𝑥 . 𝑑𝑥〗+∫1_0^4▒〖 𝑒2𝑥 . 𝑑𝑥〗 Solving I1 and I2 separately Solving I1 ∫1_0^4▒〖𝑥 𝑑𝑥〗 Putting 𝑎 =0 𝑏 =4 ℎ=(𝑏 − 𝑎)/𝑛 =(4 − 0)/𝑛 =4/𝑛 𝑓(𝑥)=𝑥 We know that ∫1_𝑎^𝑏▒〖𝑥 𝑑𝑥〗 =(𝑏−𝑎) (𝑙𝑖𝑚)┬(𝑛→∞) 1/𝑛 (𝑓(𝑎)+𝑓(𝑎+ℎ)+𝑓(𝑎+2ℎ)…+𝑓(𝑎+(𝑛−1)ℎ)) Hence we can write ∫1_0^4▒〖𝑥 𝑑𝑥〗 =(4−0) lim┬(n→∞) 1/𝑛 (𝑓(0)+𝑓(0+ℎ)+𝑓(0+2ℎ)+… +𝑓(0+(𝑛−1)ℎ) =4 lim┬(n→∞) 1/𝑛 (𝑓(0)+𝑓(ℎ)+𝑓(2ℎ)+… +𝑓((𝑛−1)ℎ) Here, 𝑓(𝑥)=𝑥 𝑓(0)=0 𝑓(ℎ)=ℎ 𝑓 (2ℎ)=2ℎ 𝑓((𝑛−1)ℎ)=(𝑛−1)ℎ Hence, our equation becomes ∴ ∫_0^4▒𝑥 𝑑𝑥 =4 lim┬(n→∞) 1/𝑛 (𝑓(0)+𝑓(ℎ)+𝑓(2ℎ)+… +𝑓((𝑛−1)ℎ) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) 1/𝑛 (0+ℎ+2ℎ+ ……+(𝑛−1)ℎ) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) 1/𝑛 ( ℎ (1+2+ ………+(𝑛−1))) We know that 1+2+3+ ……+𝑛= (𝑛 (𝑛 + 1))/2 1+2+3+ ……+𝑛−1= ((𝑛 − 1) (𝑛 − 1 + 1))/2 = (𝑛 (𝑛 − 1) )/2 = 4 (𝑙𝑖𝑚)┬(𝑛→∞) 1/𝑛 ( (ℎ . 𝑛(𝑛 − 1))/2) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) ( 𝑛(𝑛 − 1)ℎ/2𝑛) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) ( (𝑛 − 1)ℎ/2) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) ( (𝑛 − 1)4/(2 . 𝑛)) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) ( 2(𝑛/𝑛 − 1/𝑛)) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) ( 2(1− 1/𝑛)) = 4( 2(1− 1/∞)) [𝑈𝑠𝑖𝑛𝑔 ℎ=4/𝑛] = 4( 2(1−0)) = 4×2 = 𝟖 Solving I2 ∫_0^4▒𝑒^2𝑥 𝑑𝑥 Putting 𝑎 = 0 𝑏 =4 ℎ = (𝑏 − 𝑎)/𝑛 = (4 − 0)/𝑛 = 4/𝑛 𝑓(𝑥)=𝑒^2𝑥 We know that ∫1_𝑎^𝑏▒〖𝑥 𝑑𝑥〗 =(𝑏−𝑎) (𝑙𝑖𝑚)┬(𝑛→∞) 1/𝑛 (𝑓(𝑎)+𝑓(𝑎+ℎ)+𝑓(𝑎+2ℎ)…+𝑓(𝑎+(𝑛−1)ℎ)) Hence we can write ∫_0^4▒𝑒^2𝑥 𝑑𝑥 =(4−0) lim┬(n→∞) 1/𝑛 (𝑓(0)+𝑓(0+ℎ)+𝑓(0+2ℎ)+… +𝑓(0+(𝑛−1)ℎ) =4 lim┬(n→∞) 1/𝑛 (𝑓(0)+𝑓(ℎ)+𝑓(2ℎ)……+𝑓((𝑛−1)ℎ) Here, 𝑓(𝑥)=𝑒^2𝑥 𝑓(0)=𝑒^(2(0))=1 𝑓(ℎ)=𝑒^2ℎ 𝑓(2ℎ)=𝑒^(2(2ℎ))=𝑒^4ℎ 𝑓((𝑛−1)ℎ)=𝑒^2(𝑛−1)ℎ Hence we can write ∫_0^4▒𝑒^2𝑥 𝑑𝑥 =(4−0) lim┬(n→∞) 1/𝑛 (𝑓(0)+𝑓(0+ℎ)+𝑓(0+2ℎ)+… +𝑓(0+(𝑛−1)ℎ) =4 lim┬(n→∞) 1/𝑛 (𝑓(0)+𝑓(ℎ)+𝑓(2ℎ)……+𝑓((𝑛−1)ℎ) Here, 𝑓(𝑥)=𝑒^2𝑥 𝑓(0)=𝑒^(2(0))=1 𝑓(ℎ)=𝑒^2ℎ 𝑓(2ℎ)=𝑒^(2(2ℎ))=𝑒^4ℎ 𝑓((𝑛−1)ℎ)=𝑒^2(𝑛−1)ℎ Hence, our equation becomes ∴ ∫_0^4▒𝑒^2𝑥 𝑑𝑥 =4 lim┬(n→∞) 1/𝑛 (𝑓(0)+𝑓(ℎ)+𝑓(2ℎ)……+𝑓(𝑛−1)ℎ) = 4 .lim┬(n→∞) 1/𝑛 (1+𝑒^2ℎ+𝑒^4ℎ+ ……+𝑒^(2(𝑛 − 1) ℎ) ) Let S = 1+𝑒^2ℎ+𝑒^4ℎ+ ……+𝑒^(2(𝑛 − 1) ℎ) It is a G.P. with common ratio (r) r = 𝑒^2ℎ/1 = 𝑒^2ℎ We know Sum of G.P = a((𝑟^𝑛 − 1)/(𝑟 − 1)) Replacing a by 1 and r by 𝑒^2ℎ , we get S = 1(((𝑒^2ℎ )^𝑛 − 1)/(𝑒^2ℎ − 1))= (𝑒^2𝑛ℎ − 1)/(𝑒^2ℎ − 1) Thus ∴ ∫_0^4▒𝑒^𝑥 𝑑𝑥 = 4 lim┬(n→∞) 1/𝑛 (1+𝑒^2ℎ+𝑒^4ℎ+ ……+𝑒^(2(𝑛 − 1) ℎ) ) Putting the value of S, we get = 4 .lim┬(n→∞) 1/𝑛 ((𝑒^2𝑛ℎ − 1)/(𝑒^2ℎ − 1)) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) 1/𝑛 ((𝑒^2𝑛ℎ − 1)/(2ℎ . (𝑒^2ℎ − 1)/2ℎ)) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) (𝑒^2𝑛ℎ − 1)/2𝑛ℎ . 1/( (𝑒^2ℎ − 1)/2ℎ) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) (𝑒^2𝑛ℎ − 1)/2𝑛ℎ . (𝑙𝑖𝑚)┬(𝑛→∞) 1/( (𝑒^2ℎ − 1)/2ℎ) Solving (𝐥𝐢𝐦)┬(𝐧→∞) ( 𝟏)/(( 𝒆^𝟐𝒉 − 𝟏)/𝟐𝒉) As n→∞ ⇒ 2/ℎ →∞ ⇒ ℎ →0 ∴ lim┬(n→∞) ( 1)/(( 𝑒^2ℎ − 1)/2ℎ) = lim┬(h→0) ( 1)/(( 𝑒^2ℎ − 1)/2ℎ) = 1/1 = 1 Thus, our equation becomes ∫1_0^4▒〖𝑒𝑥 𝑑𝑥〗 ="4" (𝑙𝑖𝑚)┬(𝑛→∞) (𝑒^2𝑛ℎ − 1)/2𝑛ℎ . (𝑙𝑖𝑚)┬(𝑛→∞) 1/( (𝑒^2ℎ − 1)/2ℎ) " " = "4" (𝑙𝑖𝑚)┬(𝑛→∞) (𝑒^2𝑛ℎ − 1)/2𝑛ℎ . 1 = 4 (𝑙𝑖𝑚)┬(𝑛→∞) (𝑒^(2𝑛 . 4/𝑛) − 1)/(2𝑛 (4/𝑛) ) = 4 (𝑙𝑖𝑚)┬(𝑛→∞) (𝑒^8 − 1)/8 (𝑈𝑠𝑖𝑛𝑔 (𝑙𝑖𝑚)┬(𝑡→0) (𝑒^𝑡 − 1)/𝑡 =1) (𝑈𝑠𝑖𝑛𝑔 ℎ=4/𝑛) = 4 (𝑒^8 − 1)/8 = (𝒆^𝟖 − 𝟏)/𝟐 Putting the values of I1 and I2 in I ∴ I = ∫1_0^4▒〖𝑥 . 𝑑𝑥〗+∫1_0^4▒〖 𝑒2𝑥 . 𝑑𝑥〗 = 8 + (𝑒^8 − 1)/2 = (16 + 𝑒^8 − 1)/2 = (𝟏𝟓 + 𝒆^𝟖)/𝟐