Theorem 9.10 - Chapter 9 Class 9 Circles

Last updated at August 13, 2026 by

Theorem 9.10 - Sum of opposite angles in cyclic quadrilateral is 180° - Theorems

part 2 - Theorem 9.10 - Theorems - Serial order wise - Chapter 9 Class 9 Circles
part 3 - Theorem 9.10 - Theorems - Serial order wise - Chapter 9 Class 9 Circles

 

Remove Ads
Teachoo · Class 9 Explore Class 9

Transcript

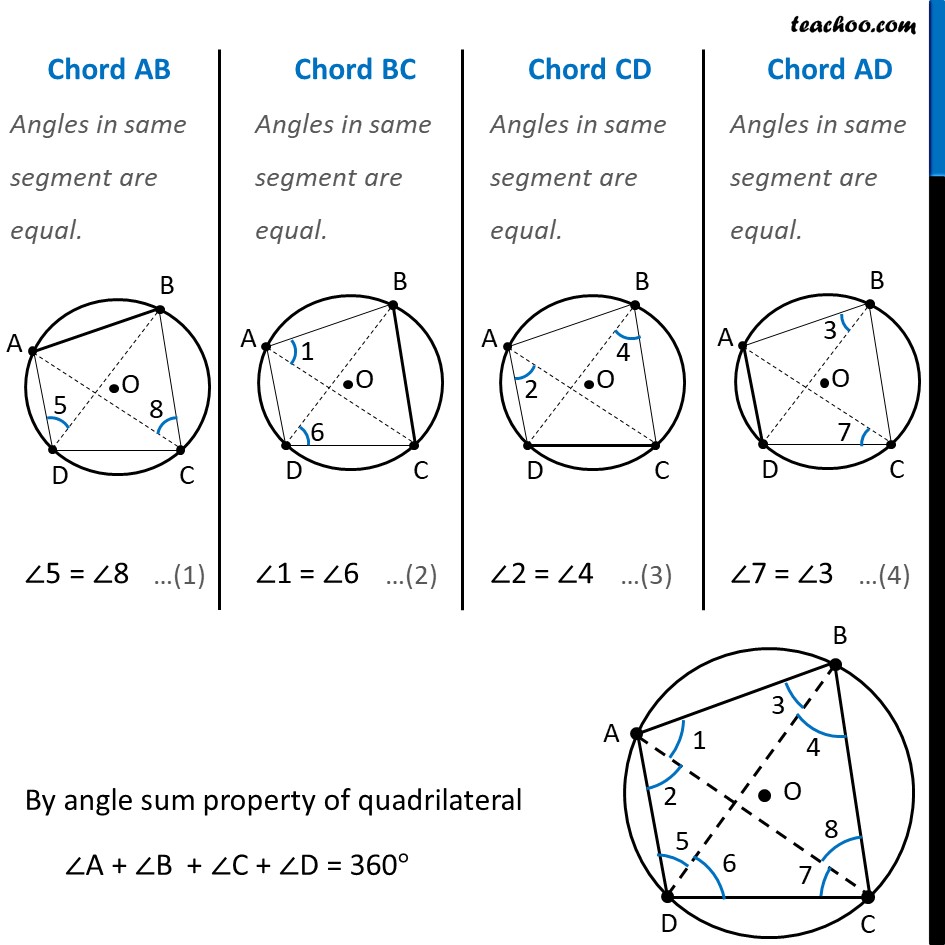
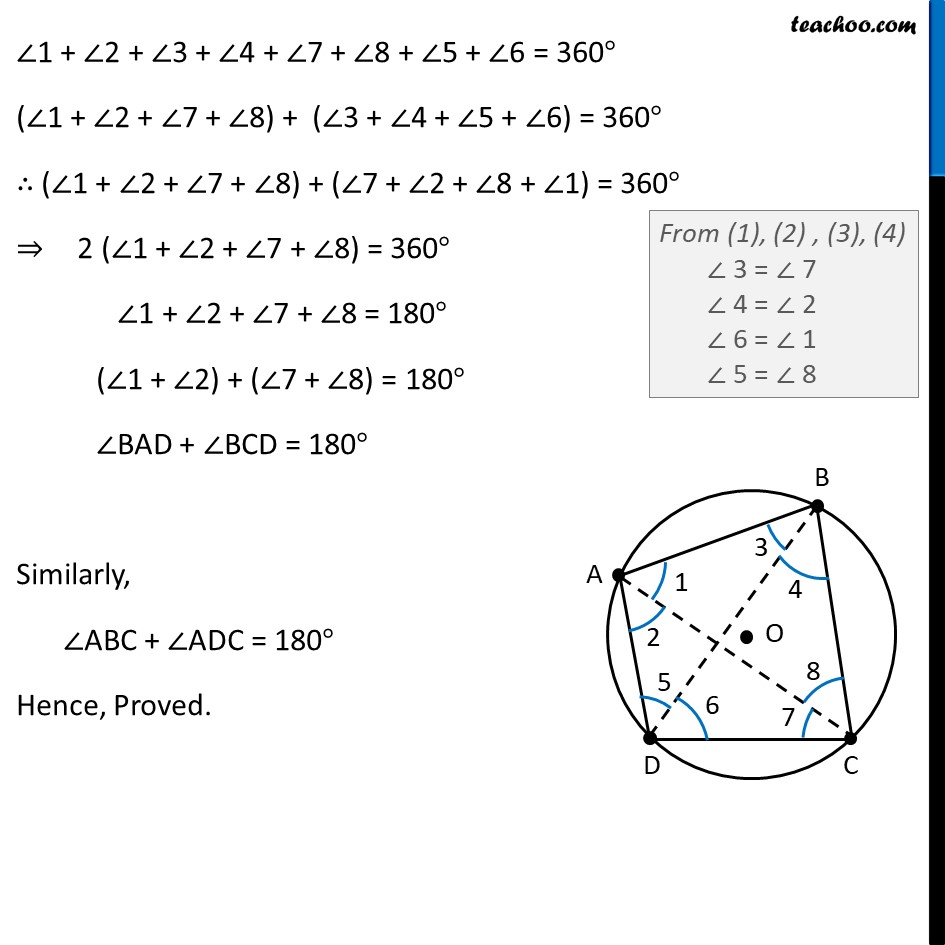
Theorem 9.11 The sum of either pair of opposite angles of a cyclic quadrilateral is 180°. Given : ABCD is a cyclic quadrilateral. of a circle with centre at O To Prove : ∠ BAD + ∠ BCD = 180° ∠ ABC + ∠ ADC = 180° Proof: Chord AB Angles in same segment are equal. ∠5 = ∠8 Chord BC Angles in same segment are equal. ∠1 = ∠6 Chord CD Angles in same segment are equal. ∠2 = ∠4 Chord AD Angles in same segment are equal. ∠7 = ∠3 ∠1 + ∠2 + ∠3 + ∠4 + ∠7 + ∠8 + ∠5 + ∠6 = 360° (∠1 + ∠2 + ∠7 + ∠8) + (∠3 + ∠4 + ∠5 + ∠6) = 360° ∴ (∠1 + ∠2 + ∠7 + ∠8) + (∠7 + ∠2 + ∠8 + ∠1) = 360° ⇒ 2 (∠1 + ∠2 + ∠7 + ∠8) = 360° ∠1 + ∠2 + ∠7 + ∠8 = 180° (∠1 + ∠2) + (∠7 + ∠8) = 180° ∠BAD + ∠BCD = 180° Similarly, ∠ABC + ∠ADC = 180° Hence, Proved. From (1), (2) , (3), (4) ∠ 3 = ∠ 7 ∠ 4 = ∠ 2 ∠ 6 = ∠ 1 ∠ 5 = ∠ 8

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh is an IIT Kanpur graduate and has been teaching for 16+ years. At Teachoo, he breaks down Maths, Science and Computer Science into simple steps so students understand concepts deeply and score with confidence.

Many students prefer Teachoo Black for a smooth, ad-free learning experience.