Theorem 10.10 - Chapter 10 Class 9 Circles (Term 2)
Last updated at Aug. 25, 2021 by Teachoo
Theorems
Theorem 10.1
Theorem 10.2 Important
Theorem 10.3 Important Deleted for CBSE Board 2023 Exams
Theorem 10.4
Theorem 10.5
Theorem 10.6 Important
Theorem 10.7
Theorem 10.8 Important
Theorem 10.9
Theorem 10.10 Important You are here
Theorem 10.11
Theorem 10.12 Important
Angle in a semicircle is a right angle Important
Chapter 10 Class 9 Circles
Serial order wise
Transcript
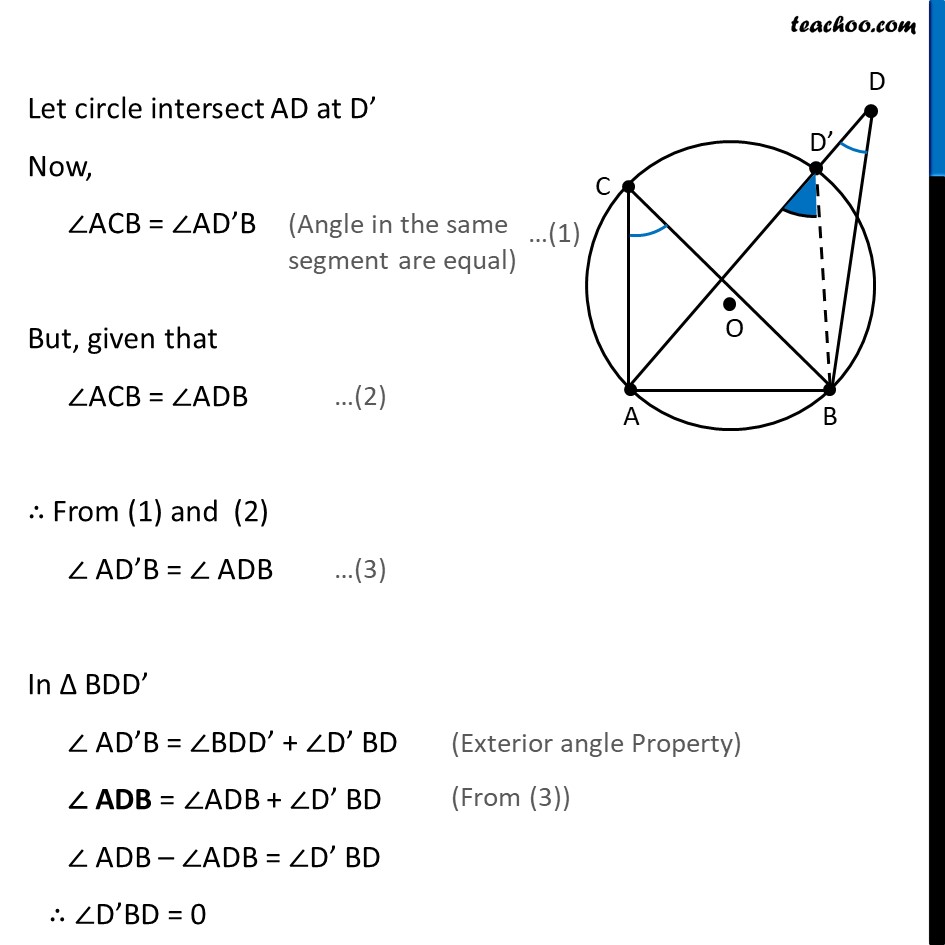
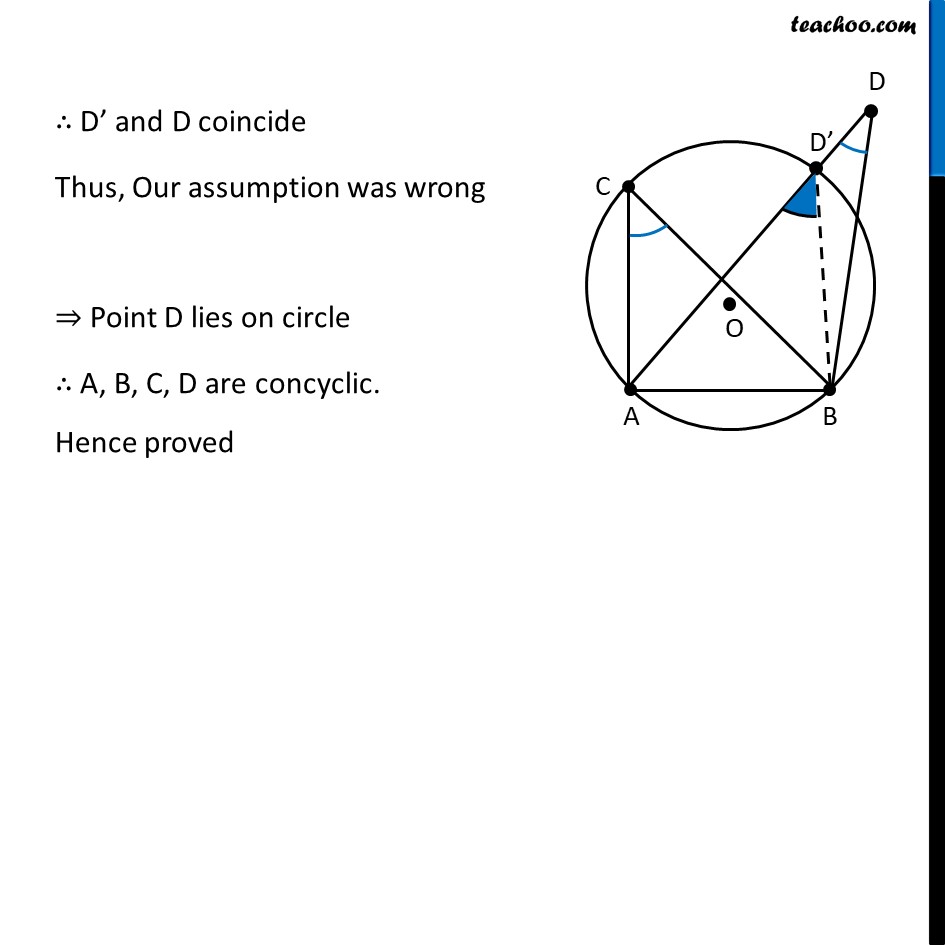
Theorem 10.10 If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic). Given : A, B, C and D are 4 points (no 3 are collinear) AB subtends equal angles at C and D i.e. ∠ACB = ∠ADB. To Prove : A,B, C and D are concylic Proof : Since A, B, C are non–collinear One circle passes through three collinear points Let us draw a circle C1 with centre at O Let us assume D does not lie on C1 Let circle intersect AD at D’ Now, ∠ACB = ∠AD’B But, given that ∠ACB = ∠ADB ∴ From (1) and (2) ∠ AD’B = ∠ ADB In ∆ BDD’ ∠ AD’B = ∠BDD’ + ∠D’ BD ∠ ADB = ∠ADB + ∠D’ BD ∠ ADB – ∠ADB = ∠D’ BD ∴ ∠D’BD = 0 ∴ D’ and D coincide Thus, Our assumption was wrong ⇒ Point D lies on circle ∴ A, B, C, D are concyclic. Hence proved
