Only 1 circle passing through 3 non-collinear points

Transcript

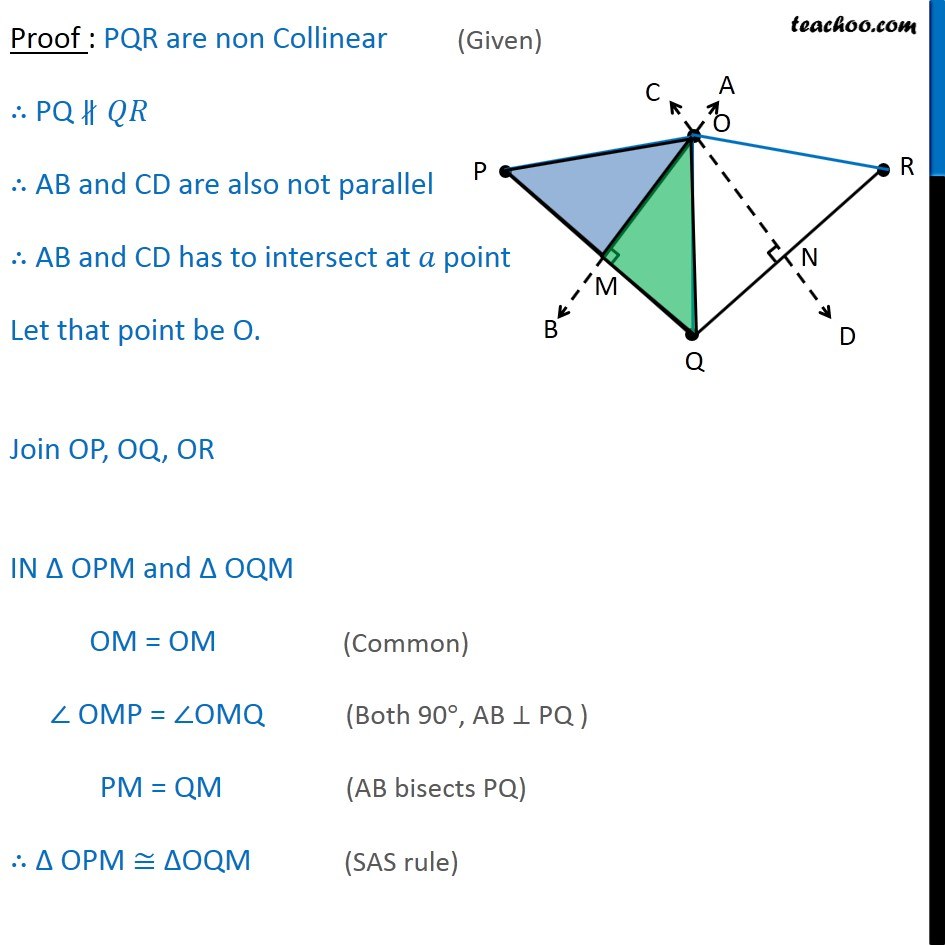
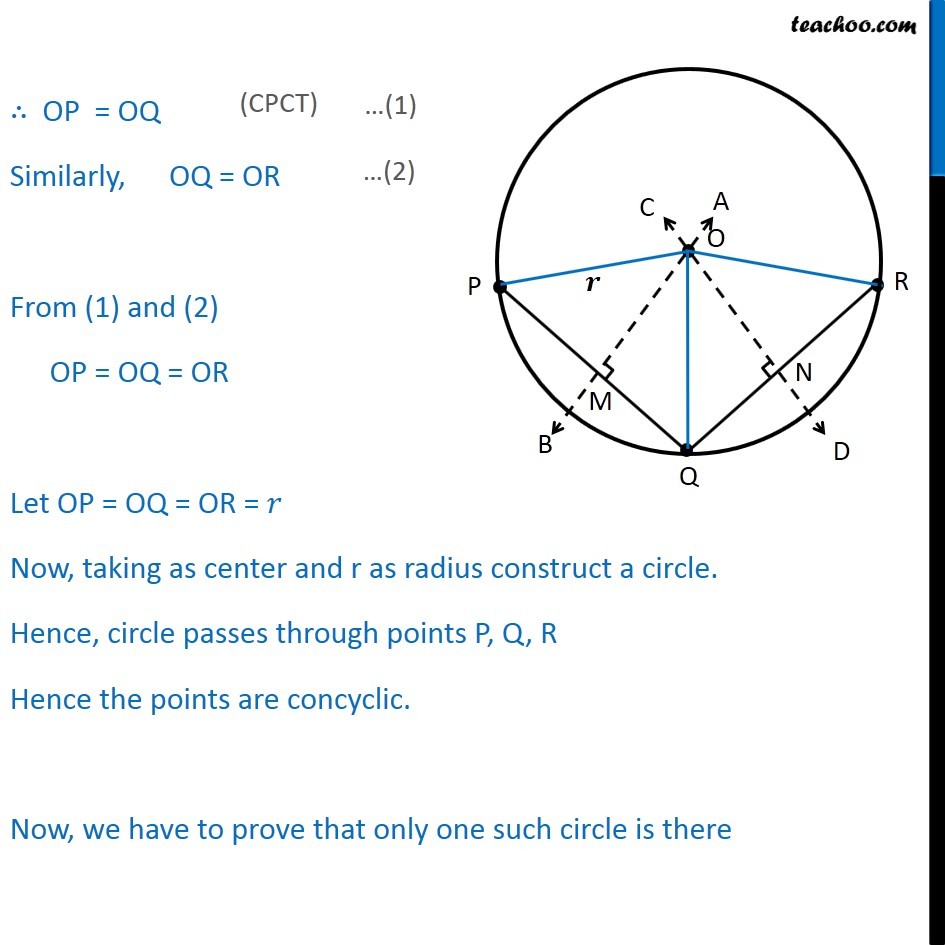
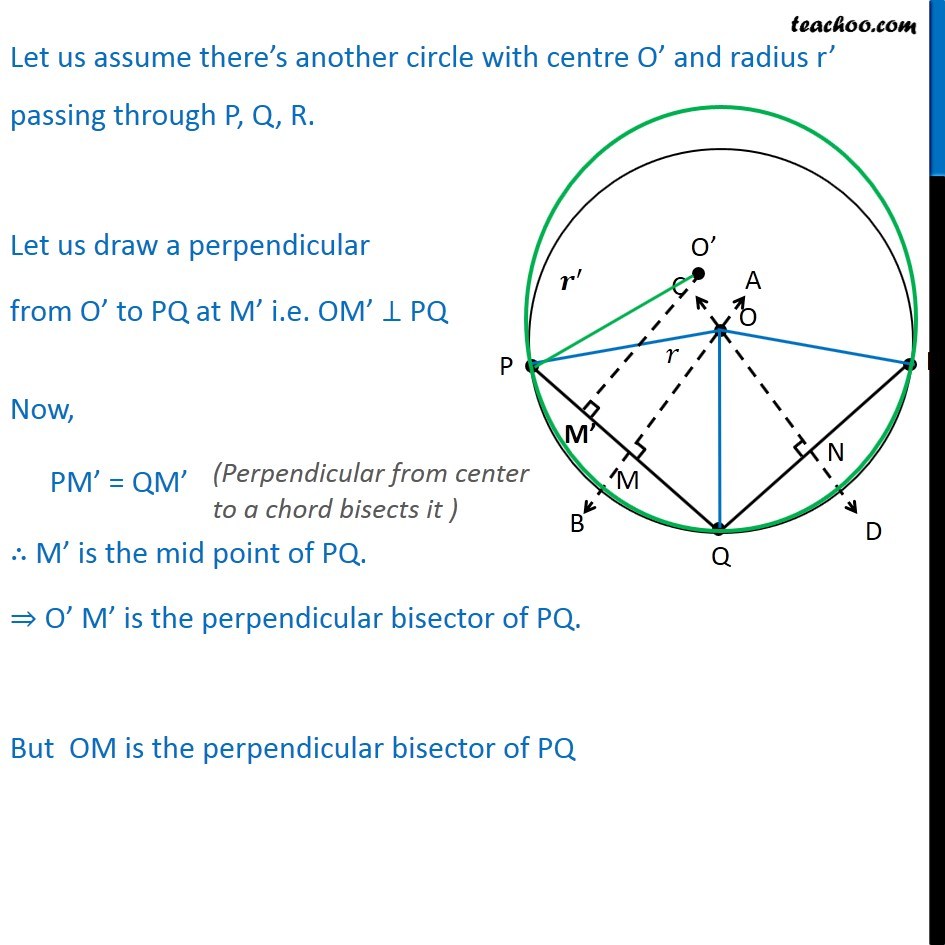
Theorem 9.5 There is one and only one circle passing through three given non-collinear points. Given : PQR are three non collinear points To Prove : Only one circle passes through PQR Construction : Draw AB perpendicular bisector of PQ at M and CD, Perpendicular bisector of QR at N Proof : PQR are non Collinear PQ AB and CD are also not parallel AB and CD has to intersect at point Let that point be O. Join OP, OQ, OR IN OPM and OQM OM = OM OMP = OMQ PM = QM OPM OQM OP = OQ Similarly, OQ = OR From (1) and (2) OP = OQ = OR Let OP = OQ = OR = Now, taking as center and r as radius construct a circle. Hence, circle passes through points P, Q, R Hence the points are concyclic. Now, we have to prove that only one such circle is there Let us assume there s another circle with centre O and radius r passing through P, Q, R. Let us draw a perpendicular from O to PQ at M i.e. OM PQ Now, OM O M PM = QM M is the mid point of PQ. O M is the perpendicular bisector of PQ. But OM is the perpendicular bisector of PQ As a line can have only one perpendicular bisector, Hence, O M coincides with OM Hence, O coincides with O Hence, only one such that circle exist that passes through points P, Q, R. Hence proved