Theorem 9.4 - Chapter 9 Class 9 Circles

Transcript

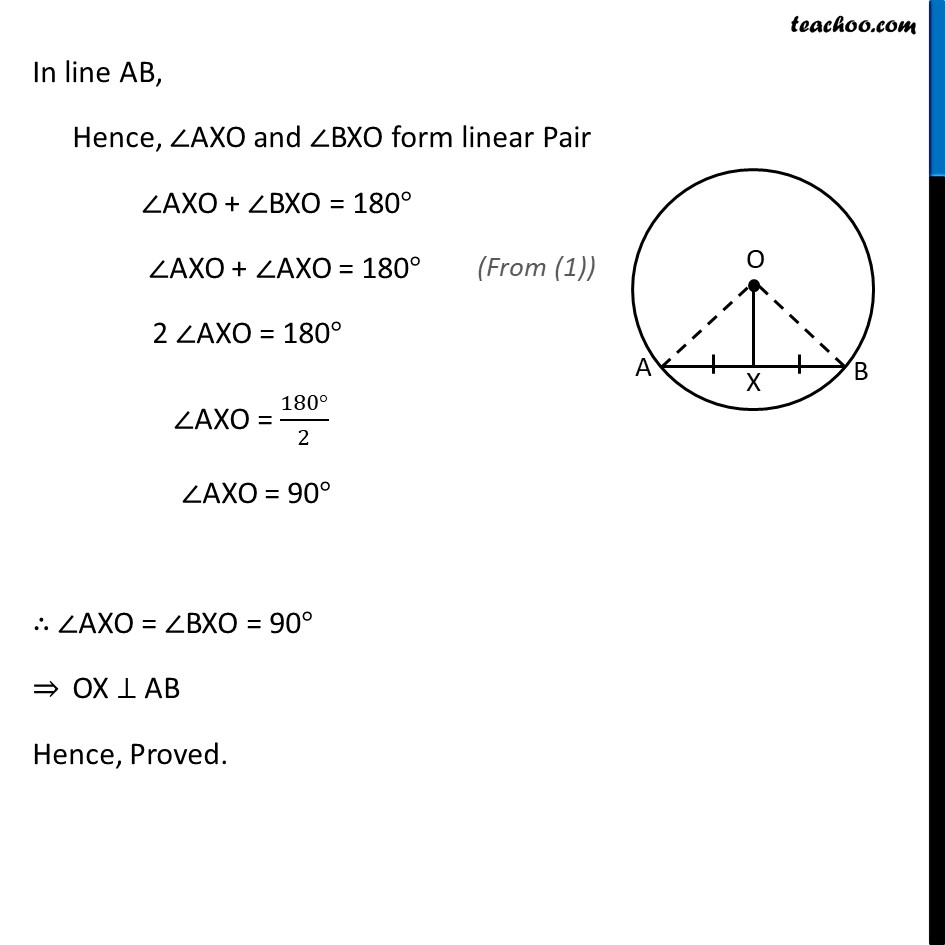
Theorem 9.4 The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord. Given : A circle with center at O. AB is chord of circle & OX bisects AB i.e. AX = BX To Prove : OX ⊥ AB Proof : In ∆AOX & ∆BOX OA = OB OX = OX AX = BX ∴ ∆AOX ≅ ∆BOX ∠ AXO = BXO In line AB, Hence, ∠AXO and ∠BXO form linear Pair ∠AXO + ∠BXO = 180° ∠AXO + ∠AXO = 180° 2 ∠AXO = 180° ∠AXO = (180°)/2 ∠AXO = 90° ∴ ∠AXO = ∠BXO = 90° ⇒ OX ⊥ AB Hence, Proved.