You are here
Question 5 (MCQ) - Finding slope of tangent/normal - Chapter 6 Class 12 Application of Derivatives
Last updated at Dec. 16, 2024 by Teachoo
Chapter 6 Class 12 Application of Derivatives
Concept wise
- Finding rate of change
- To show increasing/decreasing in whole domain
- To show increasing/decreasing in intervals
- Find intervals of increasing/decreasing
-
Finding slope of tangent/normal
- Finding point when tangent is parallel/ perpendicular
- Finding equation of tangent/normal when point and curve is given
- Finding equation of tangent/normal when slope and curve are given
- Finding approximate value of numbers
- Finding approximate value of function
- Finding approximate value- Statement questions
- Finding minimum and maximum values from graph
- Local maxima and minima
- Minima/ maxima (statement questions) - Number questions
- Minima/ maxima (statement questions) - Geometry questions
- Absolute minima/maxima
Transcript
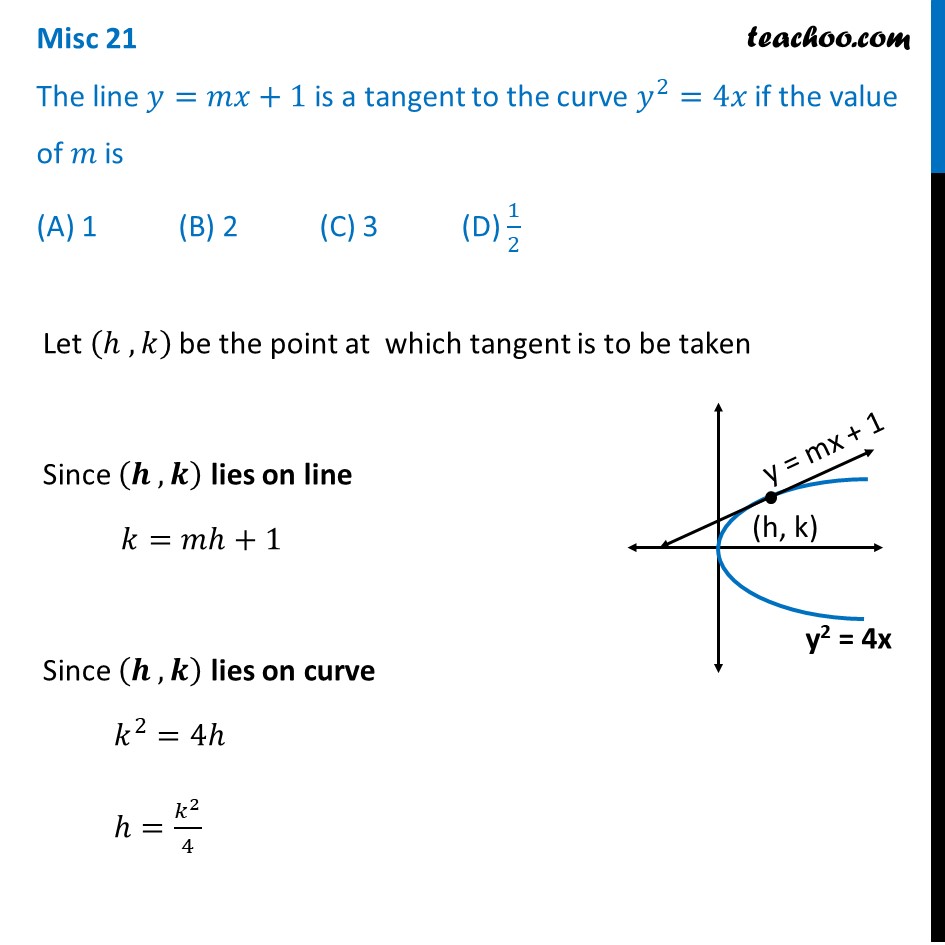
Misc 21 The line 𝑦=𝑚𝑥+1 is a tangent to the curve 𝑦^2=4𝑥 if the value of 𝑚 is (A) 1 (B) 2 (C) 3 (D) 1/2Let (ℎ , 𝑘) be the point at which tangent is to be taken & Given Equation of tangent 𝑦=𝑚𝑥+1 & Curve is 𝑦^2=4𝑥 We know that Slope of tangent to the Curve is 𝑑𝑦/𝑑𝑥 𝑦^2=4𝑥 Misc 21 The line 𝑦=𝑚𝑥+1 is a tangent to the curve 𝑦^2=4𝑥 if the value of 𝑚 is (A) 1 (B) 2 (C) 3 (D) 1/2Let (ℎ , 𝑘) be the point at which tangent is to be taken Since (𝒉 , 𝒌) lies on line 𝑘=𝑚ℎ+1 Since (𝒉 , 𝒌) lies on curve 𝑘^2=4ℎ ℎ=𝑘^2/4 Putting (2) in (1) 𝑘=𝑚(𝒌^𝟐/𝟒)+1 4𝑘=𝑚𝑘^2+4 𝑚𝑘^2−4𝑘+4=0 Since tangent touches the curve at only one point There is only one value of k So, this quadratic equation has only one root Thus, Discriminant of Quadratic equation = 0 𝒃^𝟐−𝟒𝒂𝒄=𝟎 (−4)^2−4 × 𝑚 × 4=0 16−16𝑚=0 𝑚=16/16 𝑚=1 Hence Correct Answer is (A)
