Misc 18 - Chapter 6 Class 12 Application of Derivatives

Transcript

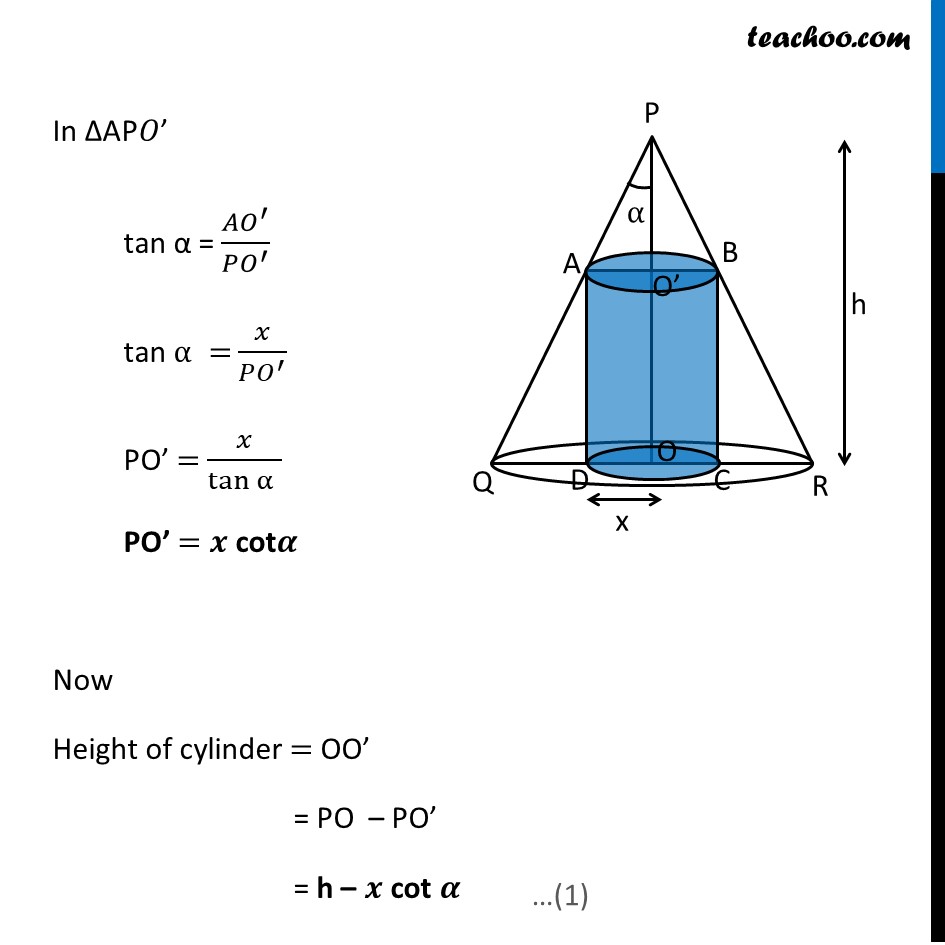
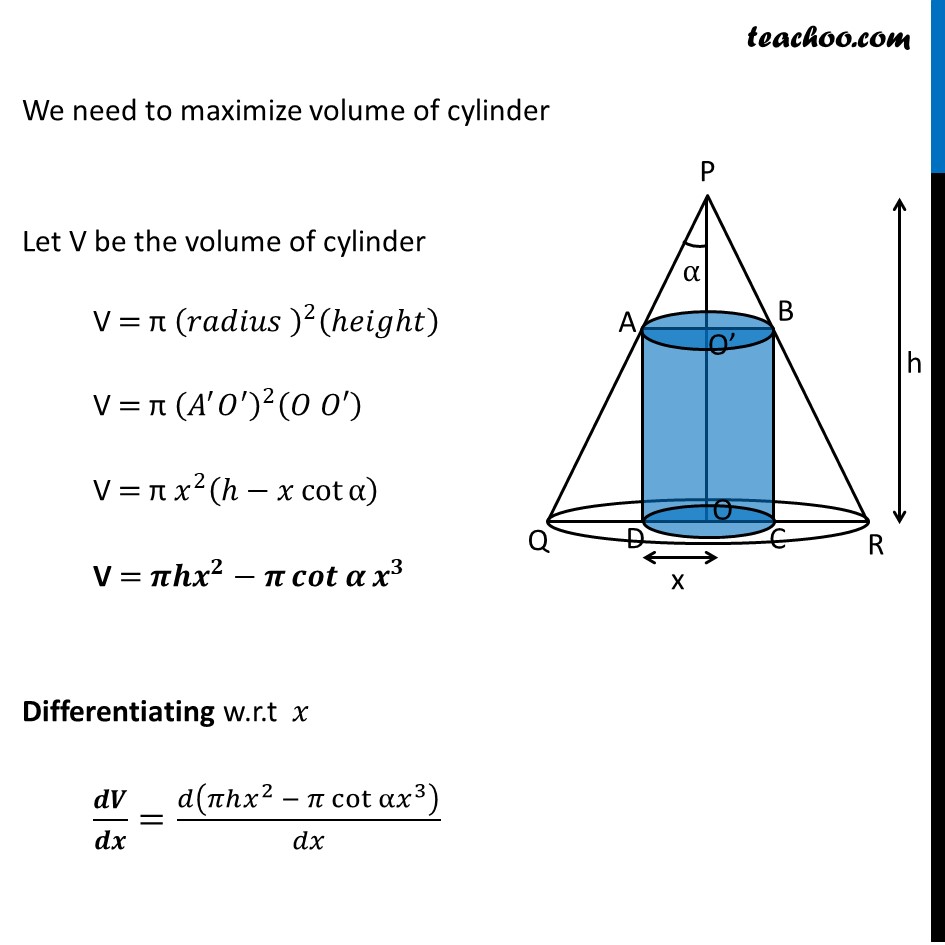
Misc 18 Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle α is one-third that of the cone and the greatest volume of cylinder is 4/27 𝜋ℎ3 tan2 𝛼Given Height of cone = h Semi-vertical angle of cone = 𝜶 Let Radius of Cylinder = 𝒙 Now, Height of cylinder = OO’ = PO – PO’ In ∆AP𝑂’ tan α = (𝐴𝑂^′)/(𝑃𝑂^′ ) tan α = 𝑥/(𝑃𝑂^′ ) PO’ = 𝑥/tan⁡α" " PO’ = 𝒙 cot𝜶 Now Height of cylinder = OO’ = PO – PO’ = h – 𝒙 cot 𝜶 We need to maximize volume of cylinder Let V be the volume of cylinder V = π (𝑟𝑎𝑑𝑖𝑢𝑠 )^2 (ℎ𝑒𝑖𝑔ℎ𝑡) V = π (𝐴^′ 𝑂^′ )^2 (𝑂 𝑂′) V = π 𝑥^2 (ℎ−𝑥 cot⁡α ) V = 𝝅𝒉𝒙^𝟐−𝝅 𝒄𝒐𝒕⁡𝜶 𝒙^𝟑 Differentiating w.r.t 𝑥 𝒅𝑽/𝒅𝒙=𝑑(𝜋ℎ𝑥^2 − 𝜋 cot⁡α 𝑥^3 )/𝑑𝑥 𝑑𝑉/𝑑𝑥= π h(𝑑(𝑥)^2)/𝑑𝑥−𝜋 cot⁡〖α.(𝑑(𝑥)^3)/𝑑𝑥〗 𝑑𝑉/𝑑𝑥= πh. 2𝑥 – π cot α. 3𝑥2 𝑑𝑉/𝑑𝑥= 2πh𝑥 – 3π cot α 𝑥2 Putting 𝒅𝑽/𝒅𝒙= 0 2π h 𝑥 – 3π cot α 𝑥2 = 0 3π cot α 𝑥2 = 2π h 𝑥 𝑥 = (2𝜋ℎ 𝑥)/(3𝜋 cot⁡〖 α.𝑥〗 ) 𝒙 = 𝟐𝒉/(𝟑 𝒄𝒐𝒕⁡〖 𝜶〗 ) Now finding (𝒅^𝟐 𝑽)/(𝒅𝒙^𝟐 ) (𝑑^2 𝑉)/(𝑑𝑥^2 )= 𝑑(2𝜋 ℎ𝑥 − 3𝜋 𝑐𝑜𝑡α . 〖 𝑥〗^2 )/𝑑𝑥 (𝑑^2 𝑉)/𝑑𝑥= 2πh – 3π cot α . 2𝑥 (𝑑^2 𝑉)/(𝑑𝑥^2 )= 2πh – 6π cot α . 𝑥 Putting value of 𝑥 = 2ℎ/(3 𝑐𝑜𝑡⁡α ) (𝑑^2 𝑉)/(𝑑𝑥^2 )= 2πh – 6π cot α × 2ℎ/(3 𝑐𝑜𝑡⁡α ) (𝑑^2 𝑉)/(𝑑𝑥^2 )= 2πh – 4πh (𝑑^2 𝑉)/(𝑑𝑥^2 )= –2πh Since (𝒅^𝟐 𝑽)/(𝒅𝒙^𝟐 )<𝟎 for 𝑥 = 2ℎ/(3 𝑐𝑜𝑡⁡α ) ∴ Volume is maximum for 𝑥 = 2ℎ/(3 𝑐𝑜𝑡⁡α ) We need to find Height and Volume For Height Height of cylinder = 𝒉 – 𝒙 cot 𝜶 = ℎ − cot 𝛼 × 2ℎ/(3 𝑐𝑜𝑡⁡〖 𝛼〗 ) = ℎ − 2ℎ/3 = 𝒉/𝟑 Hence, Height of cylinder is one third of cone Finding Maximum Volume V = π 𝑥2 (ℎ −𝑥 cot⁡α ) V = π (2ℎ/(3 cot⁡α ))^2 (ℎ−2ℎ/(3 cot⁡α ) ×cot⁡α ) V = π ((4ℎ^2)/(9 〖 cot〗^2⁡α ))(ℎ−2ℎ/3) V = π ((4ℎ^2)/(9 cot^2⁡α ))(ℎ/3) V = 4/27 ((𝜋ℎ^3)/cot^2⁡α ) V = 𝟒/𝟐𝟕 𝝅𝒉^𝟑.〖𝒕𝒂𝒏〗^𝟐⁡𝜶 Thus, greatest volume of cylinder is 4/27 𝜋ℎ^3 tan^2⁡𝛼