Chapter 6 Class 12 Application of Derivatives

Chapter 7 Class 12 Integrals →
Class 12
Important Questions for exams Class 12

Misc 10 - Chapter 6 Class 12 Application of Derivatives (Important Question)

Last updated at April 16, 2024 by

Slide1.JPG

Slide2.JPG
Slide3.JPG
Slide4.JPG

Go Ad-free

Transcript

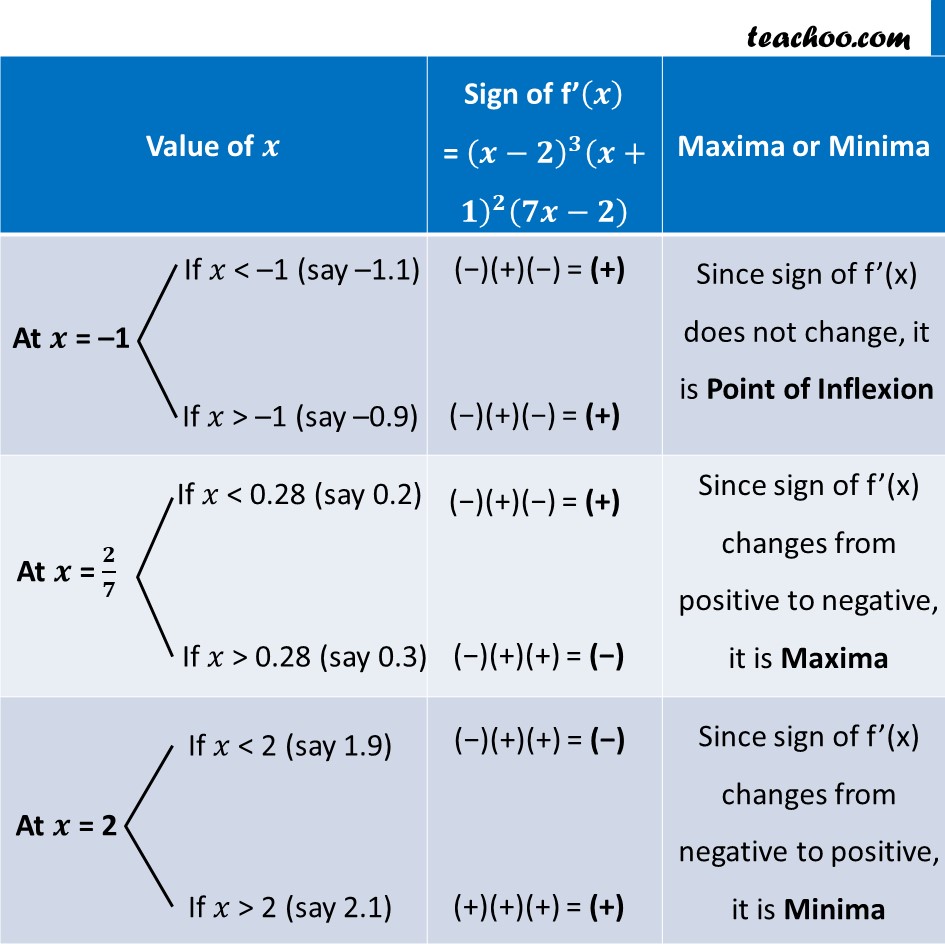
Misc 10 Find the points at which the function f given by f (𝑥) = (𝑥−2)^4 (𝑥+1)^3 has (i) local maxima (ii) local minima (iii) point of inflexionf(𝑥)= (𝑥−2)^4 (𝑥+1)3 Finding f’(𝒙) f’(𝑥) = (𝑑 ((𝑥 − 2)^4 (𝑥 + 1)^3 ))/𝑑𝑥 = 〖((𝑥−2)^4 )^′ (𝑥+1)〗^3+((𝑥+1)^3 )^′ (𝑥−2)^4 = 4(𝑥−2)^3 (𝑥+1)^3+3(𝑥+1)^2 (𝑥−2)^4 = (𝑥−2)^3 (𝑥+1)^2 [4(𝑥+1)+3(𝑥−2)] = (𝑥−2)^3 (𝑥+1)^2 [4𝑥+4+3𝑥−6] = (𝒙−𝟐)^𝟑 (𝒙+𝟏)^𝟐 [𝟕𝒙−𝟐] Putting f’(𝒙)=𝟎 (𝑥−2)^3 (𝑥+1)^2 (7𝑥−2)=0 Hence, 𝑥=2 & 𝑥=−1 & 𝑥=2/7 = 0.28 (𝑥−2)^3 = 0 𝑥 – 2 = 0 𝒙=𝟐 (𝑥+1)^2=0 (𝑥+1)=0 𝒙 = –1 7𝑥 – 2 = 0 7𝑥 = 2 𝒙 = 𝟐/𝟕 Thus, 𝑥=−𝟏 is a point of Inflexion 𝑥=𝟐/𝟕 is point of maxima 𝑥=𝟐 is point of minima

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.