Misc 10 - Chapter 6 Class 12 Application of Derivatives

Transcript

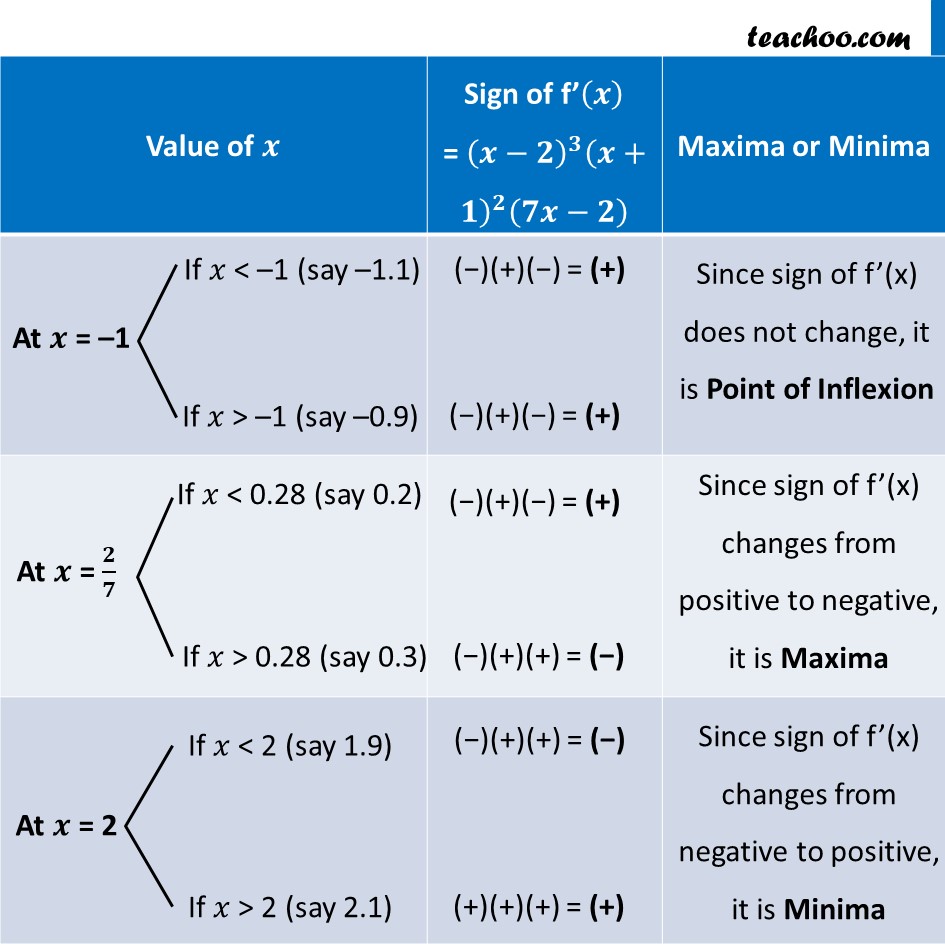
Misc 10 Find the points at which the function f given by f (𝑥) = (𝑥−2)^4 (𝑥+1)^3 has (i) local maxima (ii) local minima (iii) point of inflexionf(𝑥)= (𝑥−2)^4 (𝑥+1)3 Finding f’(𝒙) f’(𝑥) = (𝑑 ((𝑥 − 2)^4 (𝑥 + 1)^3 ))/𝑑𝑥 = 〖((𝑥−2)^4 )^′ (𝑥+1)〗^3+((𝑥+1)^3 )^′ (𝑥−2)^4 = 4(𝑥−2)^3 (𝑥+1)^3+3(𝑥+1)^2 (𝑥−2)^4 = (𝑥−2)^3 (𝑥+1)^2 [4(𝑥+1)+3(𝑥−2)] = (𝑥−2)^3 (𝑥+1)^2 [4𝑥+4+3𝑥−6] = (𝒙−𝟐)^𝟑 (𝒙+𝟏)^𝟐 [𝟕𝒙−𝟐] Putting f’(𝒙)=𝟎 (𝑥−2)^3 (𝑥+1)^2 (7𝑥−2)=0 Hence, 𝑥=2 & 𝑥=−1 & 𝑥=2/7 = 0.28 (𝑥−2)^3 = 0 𝑥 – 2 = 0 𝒙=𝟐 (𝑥+1)^2=0 (𝑥+1)=0 𝒙 = –1 7𝑥 – 2 = 0 7𝑥 = 2 𝒙 = 𝟐/𝟕 Thus, 𝑥=−𝟏 is a point of Inflexion 𝑥=𝟐/𝟕 is point of maxima 𝑥=𝟐 is point of minima