Question 13 - Examples - Chapter 6 Class 12 Application of Derivatives
Last updated at August 24, 2026 by Teachoo
Examples
Example 1
You are here
You are here
Chapter 6 Class 12 Application of Derivatives
Serial order wise
Transcript
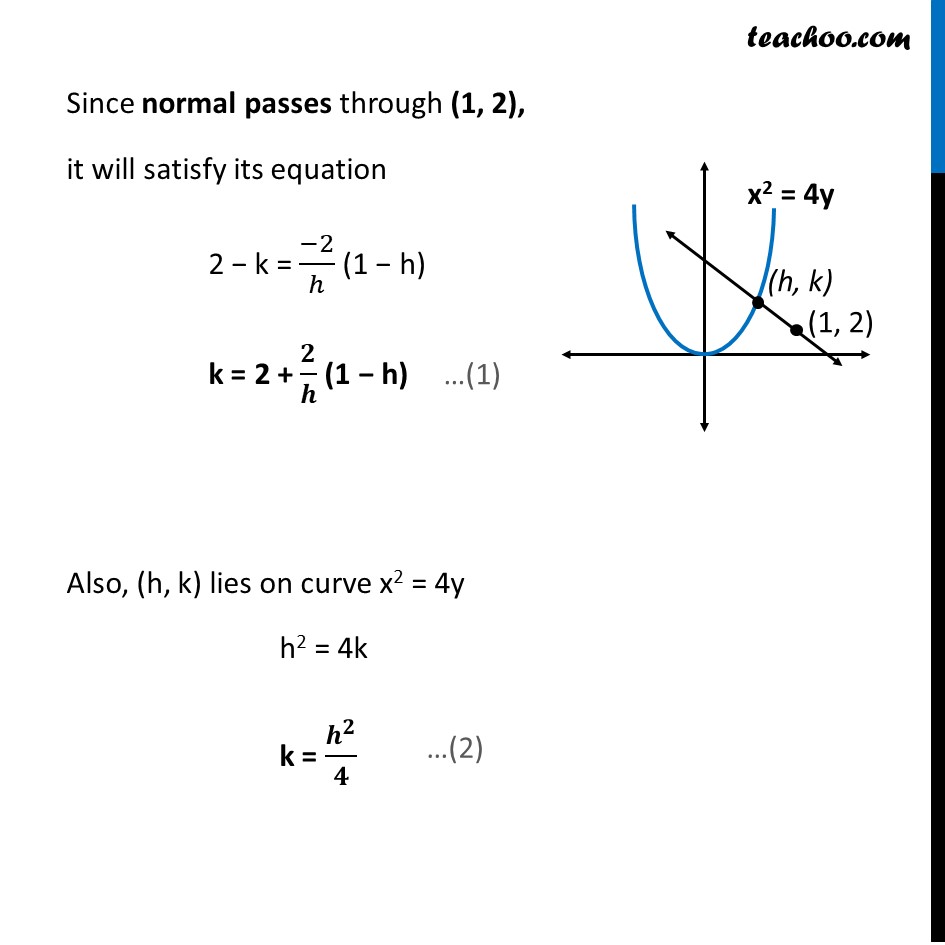
Question 13 Find the equation of the normal to the curve x2 = 4y which passes through the point (1, 2).Given Curve x2 = 4y Differentiating w.r.t. x 2x = 4𝑑𝑦/𝑑𝑥 𝑑𝑦/𝑑𝑥 = 𝑥/2 ∴ Slope of normal = (−1)/(𝑑𝑦/𝑑𝑥) = (−1)/((𝑥/2) ) = (−𝟐)/𝒙 Let (h, k) be the point where normal & curve intersect We need to find equation of the normal to the curve x2 = 4y which passes through the point (1, 2). But to find equation… we need to find point on curve Let (h, k) be the point where normal & curve intersect ∴ Slope of normal at (h, k) = (−𝟐)/𝒉 Equation of normal passing through (h, k) with slope (−2)/ℎ is y – y1 = m(x – x1) y − k = (−𝟐)/𝒉 (x − h) Since normal passes through (1, 2), it will satisfy its equation 2 − k = (−2)/ℎ (1 − h) k = 2 + 𝟐/𝒉 (1 − h) Also, (h, k) lies on curve x2 = 4y h2 = 4k k = 𝒉^𝟐/𝟒 From (1) and (2) 2 + 2/ℎ (1 − h) = ℎ^2/4 2 + 2/ℎ − 2 = ℎ^2/4 2/ℎ = ℎ^2/4 ℎ^3 = 8 h = ("8" )^(1/3) h = 2 Putting h = 2 in (2) k = ℎ^2/4 = 〖(2)〗^2/4 = 4/4 = 1 Hence, h = 2 & k = 1 Putting h = 2 & k = 1 in equation of normal 𝑦−𝑘=(−2(𝑥 − ℎ))/ℎ 𝑦−1=(−2(𝑥 − 2))/2 𝑦−1=−1(𝑥−2) 𝑦−1=−𝑥+2 𝑥+𝑦=2+1 𝒙+𝒚=𝟑
