Check sibling questions

Examples

Miscellaneous →
Chapter 6 Class 12 Application of Derivatives
Serial order wise

Example 32 - Chapter 6 Class 12 Application of Derivatives

Last updated at May 29, 2023 by

Example 44 - A man of height 2 meters walks at uniform speed

Example 44 - Chapter 6 Class 12 Application of Derivatives - Part 2
Example 44 - Chapter 6 Class 12 Application of Derivatives - Part 3 Example 44 - Chapter 6 Class 12 Application of Derivatives - Part 4

This video is only available for Teachoo black users

Subscribe Now

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

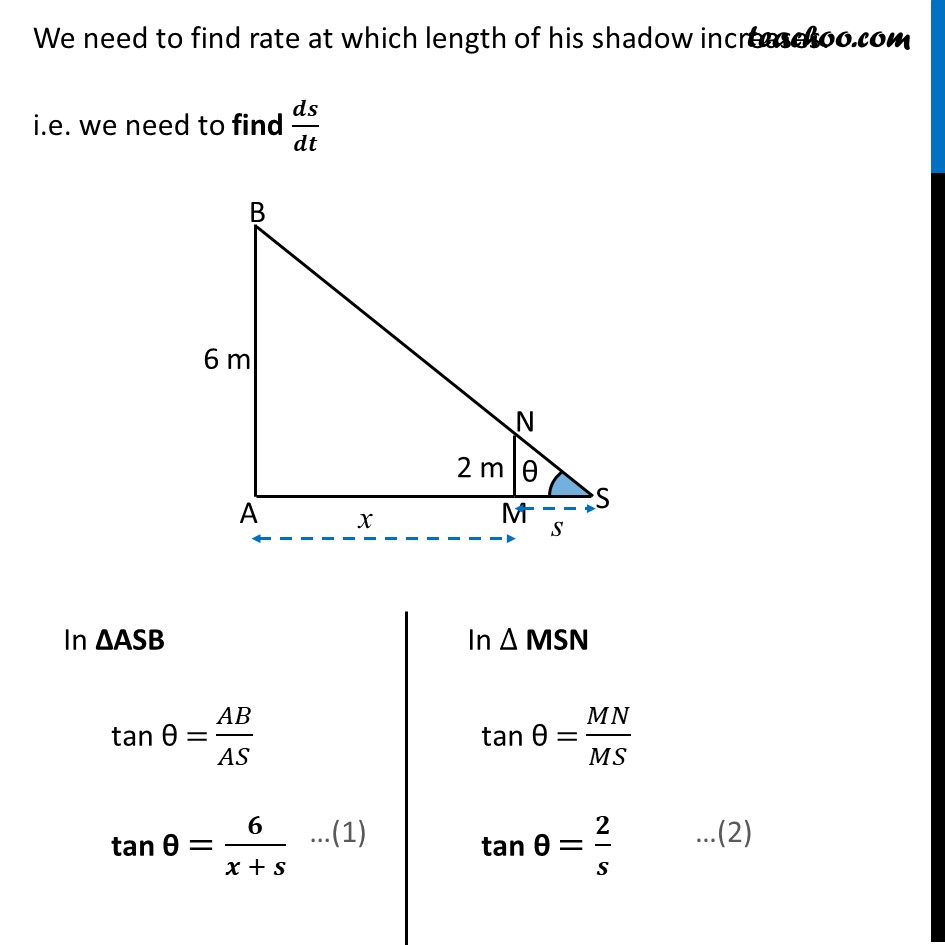
Example 32 A man of height 2 meters walks at a uniform speed of 5 km/h away from a lamp post which is 6 meters high. Find the rate at which the length of his shadow increases.Let AB be the lamp post & MN be the man of height 2m. & AM = x meter & MS is the shadow of the man Let length of shadow MS = s meter Given man walks at speed of 5 km/h ∴ 𝒅𝒙/𝒅𝒕 = 5 km/h We need to find rate at which length of his shadow increases. i.e. we need to find 𝒅𝒔/𝒅𝒕 In ΔASB tan θ = 𝐴𝐵/𝐴𝑆 tan θ =𝟔/(𝒙 + 𝒔) In ∆ MSN tan θ = 𝑀𝑁/𝑀𝑆 tan θ =𝟐/𝒔 From (1) & (2) 𝟔/(𝒙 + 𝒔) = 𝟐/𝒔 6s = 2x + 2s 6s – 2s = 2x 4s = 2x 2s = x x = 2s We need to find 𝑑𝑠/𝑑𝑡 Now, x = 2s Diff w.r.t t 𝑑𝑥/𝑑𝑡= 𝑑(2𝑠)/𝑑𝑡 𝒅𝒙/𝒅𝒕= 2.𝑑𝑠/𝑑𝑡 5 = 2 𝑑𝑠/𝑑𝑡 𝑑𝑠/𝑑𝑡 = 5/2 So, 𝒅𝒔/𝒅𝒕 = 𝟓/𝟐 km/hr. (Given 𝑑𝑥/𝑑𝑡 = 5km/hr)

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.